【数据结构初阶】排序--选择排序和交换排序
⭐博客主页:️CS semi主页
⭐欢迎关注:点赞收藏+留言
⭐系列专栏:数据结构初阶
⭐代码仓库:Data Structure
家人们更新不易,你们的点赞和关注对我而言十分重要,友友们麻烦多多点赞+关注,你们的支持是我创作最大的动力,欢迎友友们私信提问,家人们不要忘记点赞收藏+关注哦!!!
排序--选择排序和交换排序
- 前言
- 一、选择排序
-
- 1、直接选择排序
-
- (1)思路及演示
- (2)代码
- (3)特性总结
- 2、堆排序
-
- 特性总结
- 二、交换排序
-
- 1、冒泡排序
-
- (1)思路及演示
- (2)代码
- (3)特性总结
- 2、快速排序
-
- (1)hoare版本
-
- (i)思路
- (ii)代码
- (iii)时间复杂度
- (iv)优化
-
- i、随机值法
- ii、三数取中法
- (v)解决小问题
- (2)挖坑法
-
- (i)思路
- (ii)代码
- (3)前后指针
-
- (i)思路
- (ii)代码
- (4)带返回值的版本
- (5)带返回值的优化版本
-
- (i)思路
- (ii)代码
- (6)快排非递归版本
-
- (i)思路及演示
- (ii)代码
- (7)特性总结
- 总结
前言
再介绍完前面的插入排序,我们就进入选择排序和交换排序的行列,那我们闲话不多说,直接介绍选择排序。
一、选择排序
1、直接选择排序
(1)思路及演示
直接选择排序的思想是从一个数组中找到最小的数和最大的数并将最小的数放到最左端,将最大的数放到最右端,左右指针再往中间靠拢,直到两个指针相遇,那当然了,还有个很重要的细节,当我们的最大值在left的位置,这时候是需要更新一下我们的max值才可以。大家如果不相信我们演示一下为什么要更新一下max值。

控制台输出:

芜湖,大家看看是不是3夹在6和7之间,没排好序呀!我们画个图来展示一下:
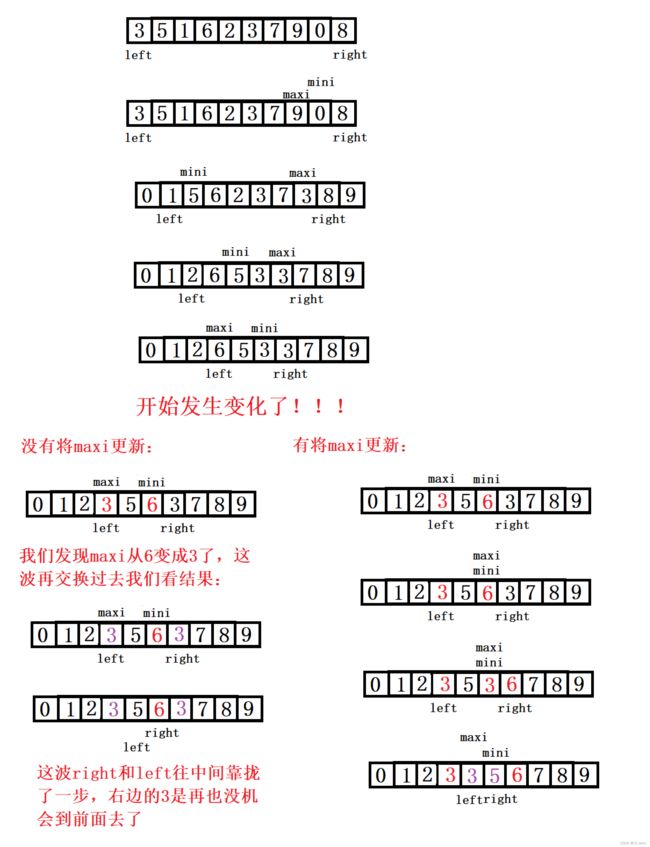
所以,我们需要判断一下此时的maxi是不是就是在left的位置,如果在的话需要更新,因为我们是先交换最小值和left的,所以我们只需要比较一次即可,如果是先交换maxi和right的话,那就需要判断mini是否在maxi的位置即可,判断一次即可。
(2)代码
//选择排序,两端向中间排序
//升序
void SelectSort(int* a, int n)
{
int left = 0;
int right = n - 1;
while (left < right)
{
int mini = left;
int maxi = left;
for (int i = left + 1; i <= right; i++)
{
if (a[i] < a[mini])
{
mini = i;
}
if (a[i] > a[maxi])
{
maxi = i;
}
}
Swap(&a[mini], &a[left]);
//如果最大值和最小值在left或者right时候,更新一下maxi的地方
if (maxi == left)
{
maxi = mini;
}
Swap(&a[maxi], &a[right]);
left++;
right--;
}
}
(3)特性总结
- 直接选择排序思考非常好理解,但是效率不是很好。实际中很少使用
- 时间复杂度:不管顺序好坏都是O(N^2),因为它是不管数据的 ,不管数据好坏都遍历两次,那就是N的二次方。
- 空间复杂度:O(1)
- 稳定性:不稳定
2、堆排序
堆排序我们在之前的博客中介绍过,这里粘一个链接大家可以跳过去看:
堆排序和Top-K问题
特性总结
- 堆排序使用堆来选数,效率就高了很多。
- 时间复杂度:O(N*logN)
- 空间复杂度:O(1)
- 稳定性:不稳定
二、交换排序
1、冒泡排序
(1)思路及演示
冒泡排序是我们日常中最常见的排序,其思路就是所谓交换,就是根据序列中两个记录键值的比较结果来对换这两个记录在序列中的位置,交换排序的特点是:将键值较大的记录向序列的尾部移动,键值较小的记录向序列的前部移动。我们通过下面演示进行讲解:
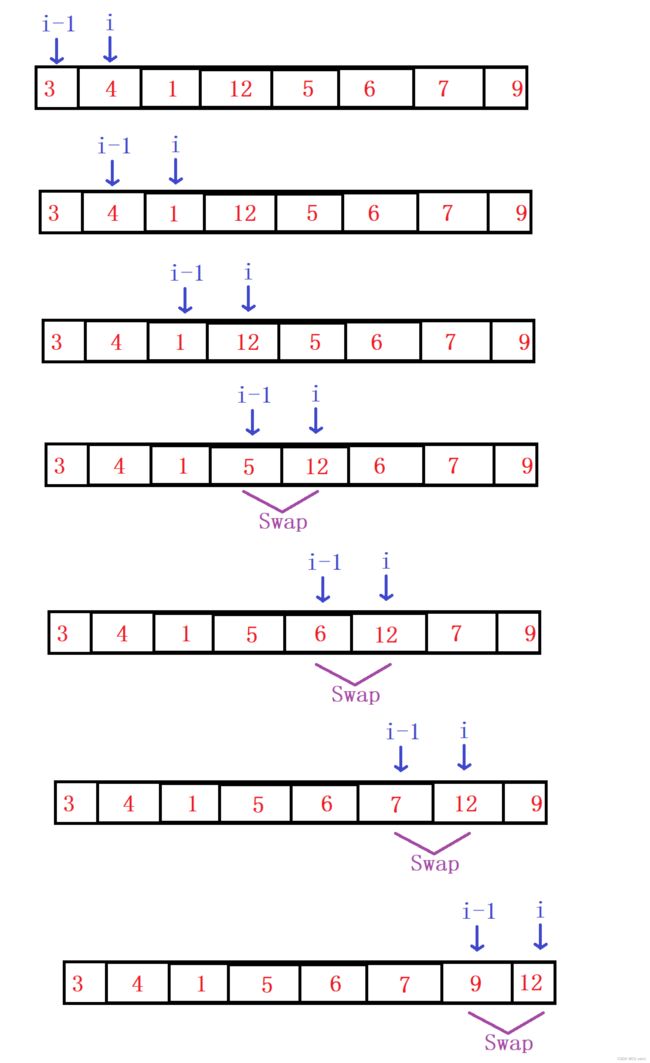
上面演示是将最大的那个数沉底沉到最末尾(一轮),我们用一个j控制次数,一次进行交换数据的是n-j次,因为第一次遍历交换是遍历了n-1次,第二次遍历交换是遍历了n-2次,我们用n-j来控制遍历次数即可。
(2)代码
//冒泡排序
void BubbleSort(int* a, int n)
{
for (int j = 0; j < n; j++)
{
int flag = 0;
//内层
for (int i = 1; i < n - j; i++)
{
if (a[i - 1] > a[i])
{
Swap(&a[i - 1], &a[i]);
flag = 1;
}
}
if (flag == 0)
{
break;
}
}
}
(3)特性总结
- 冒泡排序是一种非常容易理解的排序
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:稳定
2、快速排序

我们这里分hoare法和挖坑法以及前后指针法来进行快速排序的排序,这里讲解非常地详细,三种版本有不同的跑的速度,但是他们都属于一个量级的,是经过不断不断地优化进行的。
(1)hoare版本
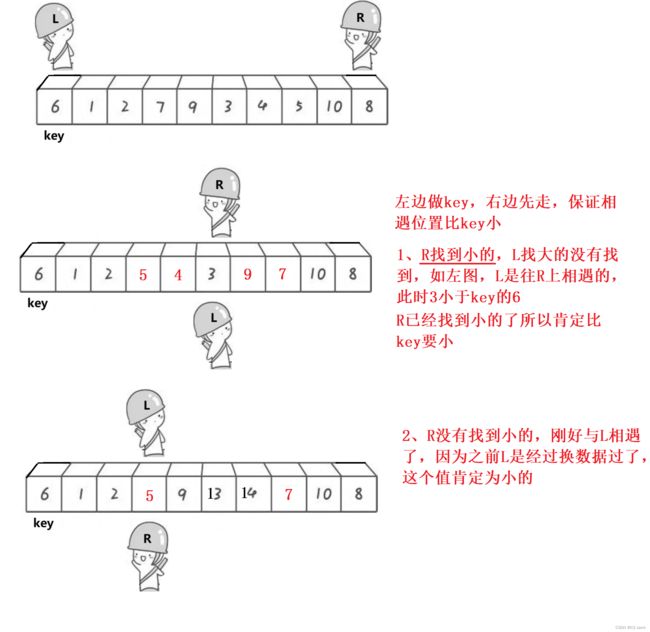
(i)思路
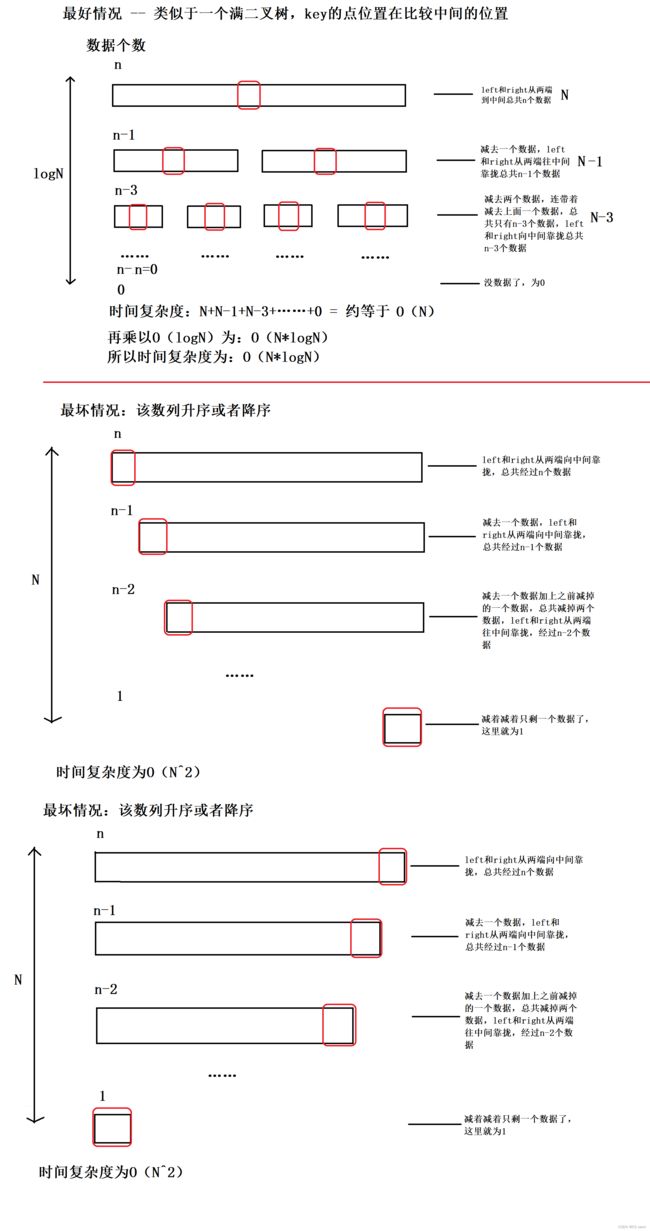
我们可以看一下hoare大佬的进行快速排序的思想,我们以最左边的数为基准key,我们left指针从最左边的key开始,right从最右边的数开始,right指针先走,找到小于等于key的数则停下,left指针再走,遇到大于等于key的数停下,再将这两个数进行交换,left和right指针再继续走,直到两指针相遇,相遇以后将left指针和基准key指针的值相交换即可。这样就是完成一轮交换了,其实这里遗留下两个问题:为何以最左边的数为key基准要right先走而不是left先走;为什么key和left指针的内容进行交换?难道不会有一种情况是key比一趟跑完的left指针所指向的内容小吗?这两个问题我们一会解决,我们看一下第一轮写完的代码: 所以我们有如下代码: 这里我们看到了不同的时间复杂度,最好情况是当我们刚好需要放入的key的地方为偏中间的位置,这样子整体的算法复杂度会降低。而当我们按照升序或者降序进行计算时间复杂度的时候,那时间复杂度会很高,因为我们删除的key元素在两端,是一个数据一个数据进行删除的。我们可以这样理解,当数组是升序的时候,我们删一个数据建立一层栈帧,这层栈帧还很大,而这样的栈帧要开n个,数据过多的时候栈区肯定是承受不住的,会导致栈溢出;而我们的key数据交换完在偏中间的位置,数据量已经减半了,而我们是先左递归再右递归的,也就是说先在左边开的栈帧数量并不多且数据量并不大,因为数据是以logN形式逐渐递减的,所以栈帧层数并不多,而当用完这一部分的栈帧以后,这些栈帧会销毁掉并还给操作系统,继续去用右边的递归,所以,类似于这种满二叉树的情况更加地快速,而且不会占据太多的栈帧位置,不会消耗太多的内存空间,所以我们就有了以下两种优化方式,也就是说将key的位置尽量交换到偏中间的位置。 该优化是对于key的取值进行优化的,因为我们上面分析的key的值在偏中间的位置时间复杂度会比较低。 利用随机值法随便定义一个在这个数组中的一个随机值randomi的下标,然后交给left下标的值交换,再按照之前的步骤进行跑程序即可。 定义left、mid和right三个下标的数,进行比较,哪个数为中间的数我们就将它与left所代表的值进行交换,再按照之前的步骤进行跑程序即可。 我们之前遗留下来的问题:为什么以left为基准值要right先走,最终left的位置的值为什么比key的位置的值小?我们画图解释一下: 我们讲解一轮的挖坑法,我们将数组最左边的数据进行保存,先走右边的R,当它遇到比key小的值那就停住,将这个数据填原本的坑,那么这个填出去的位置就为新的坑,再走左边的L,找小于原本key的位置填进去,那个填出去的位置就为新的坑了,直到L和R两个相遇,这个位置的坑需要原本存的数据填上去即可,这是一轮,要想进行更多轮的话就需要像上面horae大佬的代码一样进行分组递归即可。 大家看如下图,我们先定义prev为最左边的key位置,再定义一个cur位key的下一个位置,我们cur先走,找到比6小的值cur停下,prev走一步,两者再交换,cur继续走,遇到大于等于key的值的时候,cur继续走,prev按兵不动,当cur再次遇到比key小的值的时候,cur停住不动,prev往前走一步,进行交换,再重复之前的步骤,直到cur走出数组停止。我们这么做的理由在于我们将比key大的数卷到后面去,因为我们有两种情况,第一种情况是prev紧跟着cur,这种情况是还没找到大的数;第二种情况是prev和cur中间隔着一些大于key的值,这段区间的值都是大于key的,我们的思路是把这些大值往后卷,小值往后卷,唯一有用的方法是携家带口法,也就是prev和cur走过的路,把大的娃娃都放在中间,小的娃娃扔回家里面,中间永远夹着大的值,等出这个数组以后,此时prev指针一定到拍完序应该在的位置,因为左边的值都比它小,右边的值都比它大,所以它一定放在拍完序应该在的地方,然后利用递归解决左右区间。 其实这个带返回值是将一次递归存放到一个函数中,本质上和上面没有区别,这样我们只需要去调用函数即可: 我们发现下图,当我们最后剩6个数据的时候,我们使用快排发现要递归6次,是不是使用栈帧的空间太多了,太浪费空间了,而且这一下进行递归太麻烦了,所以我们可以进行小区间优化,当我们最终剩下个位数的数据的时候(这个数没有明确规定多少,C++库里面的数据是13左右,也有的书上定义的为7),我们直接使用插入排序即可,因为插入排序的速度很快而且很方便,比冒泡排序快好几个档次,比希尔排序更加地方便,所以我们最终选择插入排序。 这里的partsort4函数是上面所写的代码函数。 这里利用栈来解决这个问题,我们的根本思路是利用栈的先入后出的思路,将切割的小块区间放入栈再将区间拿出来进行排序即可,我们直接画图演示一下: 选择排序主要分为直接选择排序和堆排序,思想都是比较。交换排序分为,冒泡排序和快速排序,思想都是进行交换数据,这其中的时间复杂度的计算很重要,堆排序、快速排序是同一个量级的,但对于排序的速度其实取决于原本数据的好坏,虽是同一个量级,但速度还是有很大的区别的,这是对于上百万个数据而言,其中,我们的快速排序分为很多个版本,都是便于让大家理解快速排序的思想以及思路,注意区别递归版本和非递归版本,把每一个思想都理解好以后,再敲一遍代码。 家人们不要忘记点赞收藏+关注哦!!!

第一轮排序写完了,但是是不是有bug呢?我们仅仅将while那边加了附加条件是left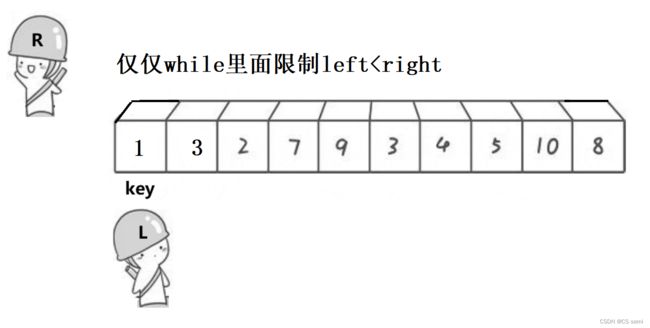
right这个指针飘到外面去了,所以我们在for的内部加入left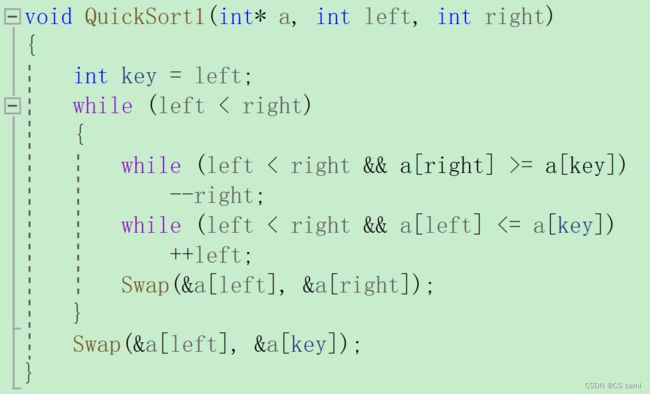
第一轮写完以后,我们还没有排好序,我们一轮排好的演示如下:
我们发现L和R两个小人站的位置的左半边刚好都是比6小的数,右半边都是比6大的数,我们有了这个思想,是不是就可以将左半边拆开,右半边再拆开成为两个区间,再进行重复的操作,将中间数放到相对应的位置即可,这就和二叉树的前序遍历有很深的关联,我们利用递归进行解决问题,左半边递归,右半边同样递归,这里我们递归返回的条件是什么?我们经过一轮发现是L这个小人和R这个小人相等的时候退出,那有没有一种可能性是L这个小人走到R这个小人后面的呢?答案是肯定的,当我们递归递归到最后只有一个格子了以后,L这个小人就会在R这个小人后面,这个是不存在的区间,是必然存在的,如下如演示:
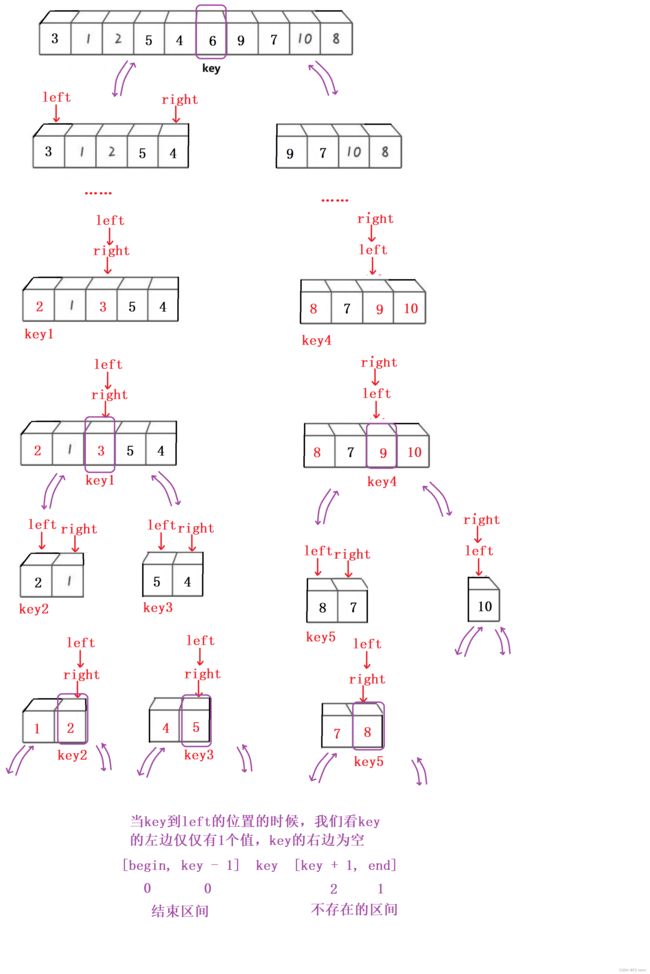
总体思路就是切区域递归,是减去key位置的递归。(ii)代码
void QuickSort1(int* a, int left, int right)
{
if (left >= right)
return;
int key = left;
int begin = left;
int end = right;
while (left < right)
{
while (left < right && a[right] >= a[key])
--right;
while (left < right && a[left] <= a[key])
++left;
Swap(&a[left], &a[right]);
}
Swap(&a[left], &a[key]);
key = left;
QuickSort1(a, begin, key - 1);
QuickSort1(a, key + 1, end);
}
(iii)时间复杂度
(iv)优化
i、随机值法
//快速排序 - 优化版本
void QuickSort1(int* a, int left, int right)
{
if (left >= right)
return;
int begin = left;
int end = right;
//优化
//随机值法
int randomi = left + (rand() % (right - left));
Swap(&a[left], &a[randomi]);
int key = left;
while (left < right)
{
while (left < right && a[right] >= a[key])
--right;
while (left < right && a[left] <= a[key])
++left;
Swap(&a[right], &a[left]);
}
Swap(&a[key], &a[left]);
key = left;
QuickSort(a, begin, key - 1);
QuickSort(a, key + 1, end);
}
ii、三数取中法
//三数取中
int GetMidNumi(int* a, int left, int right)
{
int mid = (left + right) / 2;
if (a[left] < a[mid])
{
if (a[mid] < a[right])//mid最小
{
return mid;
}
else if (a[left] > a[right])
{
return left;
}
else
{
return right;
}
}
else //a[left] >= a[mid]
{
if (a[mid] > a[right])
{
return mid;
}
else if (a[right] > a[left])
{
return left;
}
else
{
return right;
}
}
}
//快速排序 - 优化版本
void QuickSort1(int* a, int left, int right)
{
if (left >= right)
return;
int begin = left;
int end = right;
//优化
//三数取中
int middle = GetMidNumi(a, left, right);
Swap(&a[left], &a[middle]);
int key = left;
while (left < right)
{
while (left < right && a[right] >= a[key])
--right;
while (left < right && a[left] <= a[key])
++left;
Swap(&a[right], &a[left]);
}
Swap(&a[key], &a[left]);
key = left;
QuickSort(a, begin, key - 1);
QuickSort(a, key + 1, end);
}
(v)解决小问题
(2)挖坑法
(i)思路
(ii)代码
//快速排序 -- 挖坑法
void QuickSort2(int* a, int left, int right)
{
if (left >= right)
return;
int begin = left;
int end = right;
//三数取中
int middle = GetMidNumi(a, left, right);
Swap(&a[left], &a[middle]);
int key = a[left];
int hole = left;
while (left < right)
{
while (left < right && a[right] >= key)
--right;
a[hole] = a[right];
hole = right;
while (left < right && a[left] <= key)
++left;
a[hole] = a[left];
hole = left;
}
a[hole] = key;
QuickSort2(a, begin, hole - 1);
QuickSort2(a, hole + 1, end);
}
(3)前后指针
(i)思路
(ii)代码
//快速排序 -- 前后指针
void QuickSort3(int* a, int left, int right)
{
if (left >= right)
return;
int begin = left;
int end = right;
//三数取中
int middle = GetMidNumi(a, left, right);
Swap(&a[left], &a[middle]);
int key = left;
int prev = left;
int cur = left + 1;
while (cur <= right)
{
if (a[cur] < a[key])
{
++prev;
Swap(&a[cur], &a[prev]);
++cur;
}
else
{
++cur;
}
}
Swap(&a[prev], &a[key]);
key = prev;
QuickSort3(a, begin, key - 1);
QuickSort3(a, key + 1, end);
}
(4)带返回值的版本
//初始版本
int partsort1(int* a, int left, int right)
{
int key = left;
int begin = left;
int end = right;
while (left < right)
{
while (left < right && a[right] >= a[key])
--right;
while (left < right && a[left] <= a[key])
++left;
Swap(&a[left], &a[right]);
}
Swap(&a[left], &a[key]);
key = left;
return key;
}
//优化版本
int partsort2(int* a, int left, int right)
{
int begin = left;
int end = right;
//优化
//随机值法
//int randomi = left + (rand() % (right - left));
//Swap(&a[left], &a[randomi]);
//三数取中
int middle = GetMidNumi(a, left, right);
Swap(&a[left], &a[middle]);
int key = left;
while (left < right)
{
while (left < right && a[right] >= a[key])
--right;
while (left < right && a[left] <= a[key])
++left;
Swap(&a[right], &a[left]);
}
Swap(&a[key], &a[left]);
key = left;
return key;
}
//挖坑法
int partsort3(int* a, int left, int right)
{
int begin = left;
int end = right;
//三数取中
int middle = GetMidNumi(a, left, right);
Swap(&a[left], &a[middle]);
int key = a[left];
int hole = left;
while (left < right)
{
while (left < right && a[right] >= key)
--right;
a[hole] = a[right];
hole = right;
while (left < right && a[left] <= key)
++left;
a[hole] = a[left];
hole = left;
}
a[hole] = key;
return hole;
}
//前后指针法
int partsort4(int* a, int left, int right)
{
int begin = left;
int end = right;
//三数取中
int middle = GetMidNumi(a, left, right);
Swap(&a[left], &a[middle]);
int key = left;
int prev = left;
int cur = left + 1;
while (cur <= right)
{
if (a[cur] < a[key])
{
++prev;
Swap(&a[cur], &a[prev]);
++cur;
}
else
{
++cur;
}
}
Swap(&a[prev], &a[key]);
key = prev;
return key;
}
//带返回值的快速排序
void QuickSort(int* a, int left, int right)
{
if (left >= right)
{
return;
}
int keyi = partsort4(a, left, right);
QuickSort(a, left, keyi - 1);
QuickSort(a, keyi + 1, right);
}
(5)带返回值的优化版本
(i)思路
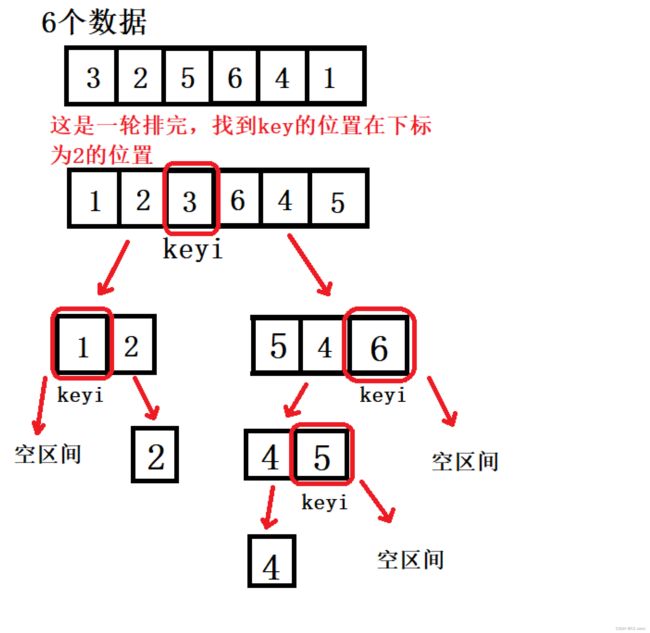
此递归区间类似于一个二叉树,如果最后那几排不进行递归而直接进行排序,那么节省的空间非常多。
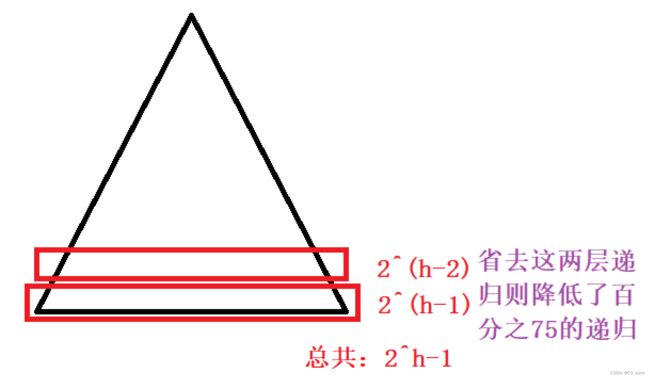
终极思路:将最后只剩10个数据使用插入排序,其余大值的数据使用快速排序。(ii)代码
//带返回值的快速排序 -- 优化版
void QuickSortp(int* a, int left, int right)
{
if (left >= right)
{
return;
}
//大区间使用快速排序
if (right - left + 1 > 10)
{
int keyi = partsort4(a, left, right);
QuickSort(a, left, keyi - 1);
QuickSort(a, keyi + 1, right);
}
//小区间直接使用插入排序
else
{
InsertSort(a + left, right - left + 1);
}
}
(6)快排非递归版本
(i)思路及演示
先入右再入左,分区间进行快速排序即可,我们这里先是进行一轮快排找到keyi的位置,再入栈为9、6和4、0。然后继续拿区间进行区间排序即可,直到这个栈为空退出销毁栈。
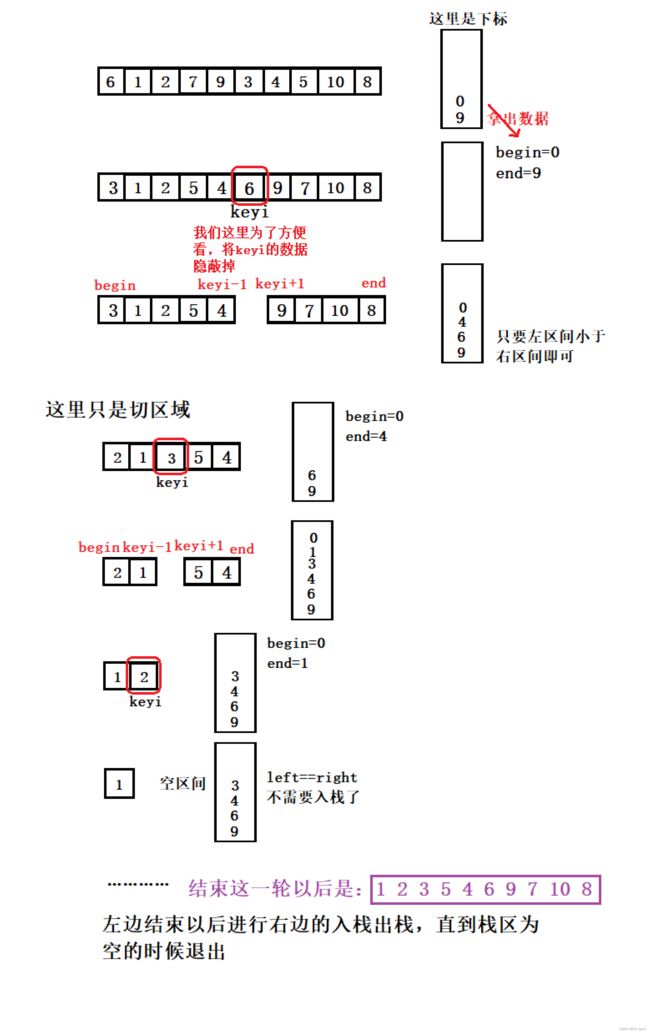
(ii)代码
//快速排序 -- 非递归版本
void QuickSortStack(int* a, int left, int right)
{
ST st;
StackInit(&st);
//先入右再入左,出栈的时候是先出左再出右
StackPush(&st, right);
StackPush(&st, left);
while (!StackEmpty(&st))
{
//取头,再取尾
int begin = StackShow(&st);//拿出栈的数据
StackPop(&st);
int end = StackShow(&st);
StackPop(&st);
//找到keyi的位置
int keyi = partsort4(a, begin, end);
//[begin, keyi-1] keyi [keyi+1, end]
//先入右再左
if (keyi + 1 < end)//中间的数大于等于两个数
{
//先右再左
StackPush(&st, end);
StackPush(&st, keyi + 1);
}
if (begin < keyi - 1)
{
//先右再左
StackPush(&st, keyi - 1);
StackPush(&st, begin);
}
}
StackDestroy(&st);
}
(7)特性总结
总结