排序——选择排序、归并排序

选择排序

选择排序是一种直观简单的排序算法，它的基本思想是：第一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，然后再从剩余的未排序元素中寻找到最小（大）元素，然后放到已排序的序列的末尾。以此类推，直到全部待排序的数据元素的个数为零。

简单选择排序

简单选择排序（Simple Selection Sort）也称为直接选择排序。

简单选择排序跟冒泡排序差不多，只不过冒泡排序是通过交换，将关键字最大的记录放在最后，而简单选择排序是选择最小的放在最前面。

具体代码：

//在这里只是提一下序列的存储结构
#define MAXSIZE 20

typedef struct					//顺序表
{
	int r[MAXSIZE+1];
	int length;
}SqList;

void SelectSort(SqList *L)
{
	for(int i=1;i < L->length;i++)
	{
		int k=i,t;
		for(int j=i+1;j <= L->length;j++)
			if(L->r[j] < L->r[i])
				k=j;
		if(k!=i)
		{
			t=L->r[i];
			L->r[i]=L->r[k];
			L->r[k]=t;
		}
	}
}

时间复杂度为$O(n^2)$，空间复杂度为$O(1)$。

由上述代码可知，在n个关键字中选出最小值，至少要进行$n-1$此比较，然后，继续在剩余的$n-1$个关键字中选择次小值并非一定要进行$n-2$次比较，若能利用前$n-1$次比较所得信息，则可减少以后各趟选择排序中所用的比较次数（最小关键字还是得至少比较$n-1$次，只是其余的次小关键字的比较次数可以被优化）。而这就要用到树形选择排序了。

树形选择排序

树形选择排序（Tree Selection Sort），又称锦标赛排序（Tournament Sort）。那么什么又是锦标赛排序呢？这个就相当于对一群参赛选手，两两进行比赛，赢的晋级，直至最后选出冠军。它的前提是，若甲能胜乙，乙能胜丙，则甲一定能胜丙。也就是说在上述的一场比赛中，亚军只能产生在输给冠军的选手中，季军只能产生在输给亚军的选手中。

假设我们通过让一个记录序列来进行比赛，选出有最小关键字的记录。例如对$$\{49,38,65,97,76,13,27,50\}$$
进行比赛，则这棵树上的叶子结点即和上面数字一一对应，如下图：
最后，数字13取得了冠军。那么进而我们要选出亚军，也就是次小关键字，由前面可知，亚军只会输给冠军，亚军也只能从输给冠军的选手里面选出，那么这时，我们将冠军删除或者把它视为比不过亚军，那么亚军进而就可以成为一棵树的根结点（冠军的位置），就选出来了。如下图：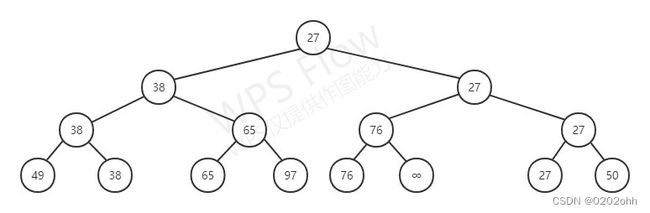
为了选出季军，我们只需要将亚军给删除或者视亚军一定比不过季军即可，如下图：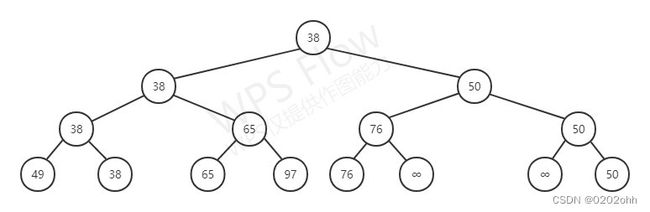
那么这就是树型选择排序，除了最小关键字外，每选择一个次小关键字仅需进行$\lceil lo{g}_{2}n\rceil +1$次比较，因此，它的时间复杂度为$O(nlo{g}_{2}n)$。但是，这种排序方法辅助存储空间较多、和最大值进行了多余的比较。为了改进这些缺点，堆排序就出来了。

堆排序

因为堆排序是为了改进树形选择排序的一些缺点，所以堆排序（Heap Sort）也是一种树形选择排序。在排序过程中，我们要将待排序记录看成是一棵完全二叉树的顺序存储结构。

首先我们要搞明白堆的定义，理解了其定义后，后面的算法就不难学习。

堆的定义

首先我们要对一棵完全二叉树进行层次遍历，然后得到它的层次遍历序列，如下图：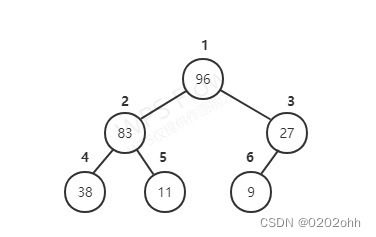
上面关键字的序列就是$\{96,83,27,38,11,9\}$，我们再仔细一看，可以发现每个结点的左子树结点的序号为该结点序号的2倍，右子树结点的序号为该结点序号的2倍+1。例如83的序号为2，它左子树结点38的序号为4，右子树结点11的序号为5。

上图就是一个堆，且是大根堆。

由此，我们可以给出堆的定义，对于$n$个元素的序列$\{k_1,k_2,...,k_n\}$，当满足下面的条件时可以被称为堆：$$1.k_i\ge k_{2i}且k_i\ge k_{2i+1}2.k_i\le k_{2i}且k_i\le k_{2i+1}$$
满足条件1的被称为大根堆，满足条件2的被称为小根堆。

就对上图的关键字序列$\{96,83,27,38,11,9\}$来说，也满足堆的条件。$96\ge 83,27$，$83\ge 38,11$。

那么堆排序到底是怎样排序的呢？堆排序的结果又是什么？
以大根堆排序为例，对一个大根堆进行排序的结果可以得到一个递增的有序序列。

大根堆的排序步骤如下：

1. 先将一个待排序的序列$r[1],r[2],...,r[n]$调整为一个大根堆，然后交换$r[1]$和$r[n]$，这样，最大的一个关键字就排到了最后
2. 再将$r[1],r[2],...,r[n-1]$重新调整为大根堆，再交换$r[1]$和$r[n-1]$，这是第二大的数就排到了倒数第二个位置
3. 一直循环，直到交换了$r[1]$和$r[2]$为止，到此就得到了一个递增的序列

同样，可以通过构造小根堆得到一个递减的有序序列。

虽然说堆排序的步骤看起来如此简单，但其中我们需要解决两个比较难的问题：

1. 如何将一个无序序列建成一个堆？
2. 交换元素之后，如何将剩余元素调整为一个新的堆？

我们把将一个无序序列建成一个堆的操作叫建初堆，把将剩余元素调整为一个新的堆的操作叫调整堆。由于建初堆需要用到调整堆的操作，下面先学习一下调整堆的操作。

调整堆

例如下图就是一个堆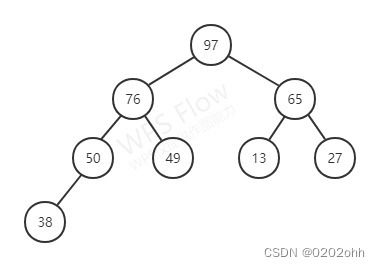
它的序列为$\{97,76,65,50,49,13,27,38\}$，将$r[1]$和$r[8]$交换后，如下图所示：

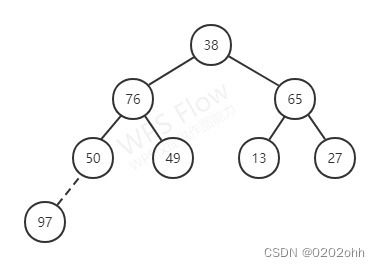
此时，除根结点外，其余结点都满足堆的性质，为了将$r[8]$除外的其余关键字调整为大根堆的形式，我们只需对自上至下进行一条路径上的结点调整即可（因为它们之间有2倍和2倍+1的关系）。首先说以堆顶元素38与其左右子树根结点的值进行比较，由于左子树根结点的值大于右子树根结点的值，则将38和76交换，如下图：
但这时以38为根的子树又不满足堆的定义了，所以还得继续调整，如下图：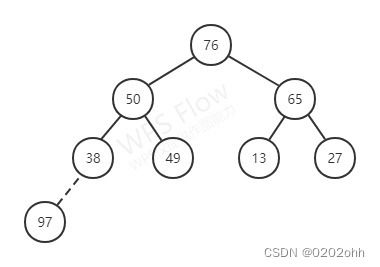
这时候就满足堆的定义了，于是又开始交换$r[1]$和$r[7]$…

综上，调整对实际上就是对下图这样一个结构进行调整，根结点上为3个结点中最大的值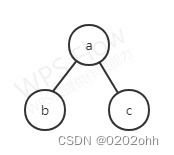
如果调整将a调整到了b的位置上，此时以a为根的子树又不满足堆的定义，于是再像这样调整即可。要时刻记住根结点和它左右子树根结点之间满足的关系。

假设经过一次交换后，得到序列$r[s],r[s+1],...,r[m]$，此时它并不满足堆的定义，但排除$r[s]$后的序列$r[s+1],...,r[m]$是满足堆的定义的。由此，具体代码如下：

void HeapAdjust(SqList *L,int s,int m)
{
	rc=L->r[s];						//保存它的副本
	for(int i=2*s;i<=m;i*=2)
	{
		if(i<m && L->r[i] < L->r[i+1])
			i++;					//找出根结点左右子树根结点的较大者
		if(rc > L->r[i])			//再与根结点比较，若小于根结点，则满足堆的定义
			break;
		L->r[s]=L->r[i];			//若不满足堆的定义，则将左右子树根结点较大者与根结点交换
		s=j;						//根结点交换后的位置
	}
	L->r[s]=rc;						//因为前面把根结点覆盖了，所以这时用它的副本来赋值
}

建初堆

要将一个无序序列调整为堆，就必须将其所对应的完全二叉树中以每一结点为根的子树都调整为堆。而在完全二叉树中，所有序号大于$\lfloor n/2\rfloor$的结点都是叶子结点（没有左右子树），因此以这些结点为根的子树均已是堆。如此，我们只需从最后一个分支结点$\lfloor n/2\rfloor$开始，依次将序号为$\lfloor n/2\rfloor 、\lfloor n/2\rfloor -1、..、1$的结点作为根的子树都调整为堆即可。

如此，我们只需反复调用上面函数即可。

具体代码：

void CreateHeap(SqList *L)
{
	int n=L->length;
	for(int i=n/2;i>0;i--)
		HeapAdjust(&L,i,n);
}

算法实现

前面两个问题都解决了之后，接下来就是真正的堆排序算法了。根据前面的描述的大根堆排序步骤，算法实现也很简单。

具体代码：

void HeapSort(SqList *L)
{
	int i,x;
	CreateHeap(&L);
	for(i=L->length;i>1;i--)
	{
		x=L->r[1];
		L->r[1]=L->r[i];
		L->r[i]=x;
		HeapAdjust(&L,1,i-1);
	}
}

在最坏的情况下，该算法的时间复杂度也为$O(nlo{g}_{2}n)$，研究表明，平均性能接近于最坏性能。它的空间复杂度为$O(1)$。

总结

选择排序就是通过选择有最小或最大关键字值的记录，将它们先放进已排好的序列。选择排序有两种方式，分别是简单选择排序和堆排序。简单选择排序就是以某个值为标准，通过不断比较选择出有最小关键字值的记录，然后放在已排好序列的最后，它在比较的时候浪费的时间比较多，算法的时间复杂度为$O(n^2)$。但它不仅可用于顺序存储结构，也可用于链式存储结构。而堆排序，是树形排序中的一个特殊情况，相较于树形选择排序，堆排序有了很大的改进，较节约了存储空间，也少了多余的比较。堆排序主要是要用到完全二叉树层次遍历的思想，只要自己动手画一画堆的树型结构图，还是很好理解的。堆排序的时间复杂度相较于简单选择排序就小多了，最坏情况下也只有$O(nlo{g}_{2}n)$。但它是不稳定的排序，同时也只能用于顺序结构，不能用于链式结构。因为它在初始建堆的时候比较的次数比较多，所以记录数较少时不宜采用，适用于记录数较多的情况。

归并排序

归并排序（Merging Sort）就是将两个或两个以上的有序表合并成一个有序表的过程。将两个有序表合并成一个有序表的过程称为2-路归并。

归并排序的基本思想是：假设初始序列含有$n$个记录，则可看成是$n$个有序的子序列，每个子序列的长度为1，然后两两并归，得到$\lceil n/2\rceil$个长度为2或1的有序子序列；再继续两两并归，…，直到得到一个长度为$n$的有序序列为止。

例如，对一个待排序记录的关键字序列$\{49,38,65,97,76,13,27\}$，它的2-路归并排序的过程如下图：
由上图可知，2-路归并是将待排序序列中前后相邻的两个有序序列归并为一个有序序列。

由于2-路归并是一个由小到大的过程，貌似跟递归又有点关系，要搞清楚归并算法，我们不妨首先来写一下将相邻两个有序序列合并在一起的算法，有了一个算法，在归并算法里，也就能调用这个算法，少了些麻烦。

对于两个序列的合并，在C语言中，我们是不能简单地将这两个序列相加就完事了，但是利用辅助空间来将一个序列中全部元素填到另一个序列中又太麻烦，我们可以另设一个序列，大小为这个两个序列的大小之和，由此，经过这两个序列中的元素比较，就将较小的放入新设的序列中。但是这样又会造成一个问题，比较中较大的元素可能不会被放进去，所以我们在最后还要将这两个序列中剩余的元素放进去才行。

具体代码：

void Merge(int R[],int T[],int low,int mid,int high)
{
	int i=low,j=mid+1,k=low;		//k是另设序列的指针
	while(i<=mid&&j<=high)
	{
		if(r[i]<=r[j])
			T[k++]=R[i++];
		else
			T[k++]=R[j++];
	}
	//比较完后，将每个序列剩余的元素放入T数组中
	while(i<=mid)
		T[k++]=R[i++];
	while(j<=high)
		T[k++]=R[j++];
}

在学习的时候我对将剩余元素复制到$T$数组中有点疑问，没想明白是怎么操作的。

由代码可知，这两个序列都有一个标识位置的指针， 且只有在比较后，较小的那个元素所在序列的指针才会自加，不然它就会一直停在那不动。想明白这点后就能理解了。

相邻两个有序子序列的合并理解清楚了之后，归并排序的算法就好理解了。

算法实现

我们在这里借用的是2-路归并，是最简单的一种，除此之外还有多路归并的情况。那么2-路归并我们是一直将一个序列不停地拆分，直到序列长度等于1，也就是每个序列只有一个元素的情况。此时递归就结束了，然后就开始一步一步地合并。

具体代码：

void MSort(int R[],int T[],int low,int high)
{
	int mid,S[MAXSIZE];
	//递归结束条件
	if(low==high)
		T[low]=R[low];
	else
	{
		mid=(low+high)/2;				//求出当前序列的分裂点
		MSort(R,S,low,mid);				//对子序列R[low],...,R[mid]递归归并排序，结果放入S[low],...,S[mid]
		MSort(R,S,mid+1,high);			//对子序列R[mid+1],...,R[high]递归归并排序，结果放入S[mid+1],...S[high]
		Merge(S,T,low,mid,high);		//将S[low],...,S[mid]和S[mid+1],...,S[high]归并到T[low],...T[high]
	}
}

void MergeSort(SqList *L)
{
	MSort(L->r,L->r,1,L->length);
}

归并算法的时间复杂度为$O(nlo{g}_{2}n)$，空间复杂度为$O(n)$。

该算法的特点在于它是稳定的一种排序方法，可用于链式存储结构。