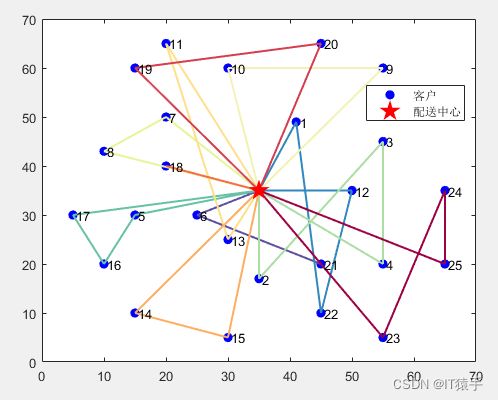
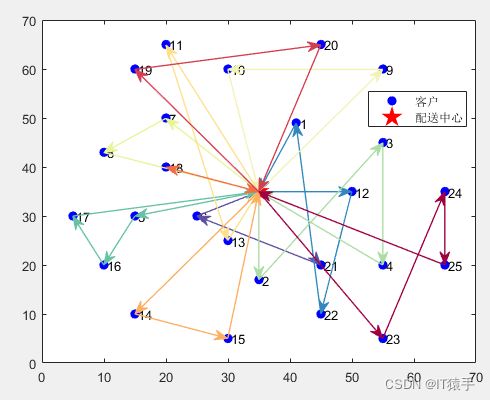
VRPTW:蜣螂优化算法DBO求解带时间窗的车辆路径问题(Vehicle Routing Problem with Time Windows, VRPTW)提供MATLAB代码
一、VRPTW
1.1模型简介
带时间窗的车辆路径问题(Vehicle Routing Problem with Time Windows, VRPTW)是车辆路径问题(VRP)的一种拓展类型。VRPTW一般指具有容量约束的车辆在客户指定的时间内提供配送或取货服务,在物流领域应用广泛,具有重要的实际意义。VRPTW常规模型如下:VRPTW模型详细介绍
min f ( x ) = 1000 ∑ k ∈ K ∑ j ∈ Δ + ( 0 ) x 0 j k + ∑ k ∈ K ∑ ( i , j ) ∈ A c i j x i j k ∑ k ∈ K ∑ j ∈ Δ + ( i ) x i j k = 1 ∀ i ∈ N ( 1 ) ∑ j ∈ Δ + ( 0 ) x 0 j k = 1 ∀ k ∈ K ( 2 ) ∑ i ∈ Δ − ( j ) x i j k − ∑ i ∈ Δ + ( j ) x j i k = 0 ∀ k ∈ K , ∀ j ∈ N ( 3 ) ∑ i ∈ Δ Δ − ( n + 1 ) x i , n + 1 , k = 1 ∀ k ∈ K ( 4 ) w i k + s i + t i j − w j k ≤ ( 1 − x i j k ) M i j , ∀ k ∈ K , ∀ ( i , j ) ∈ A ( 5 ) a i ( ∑ j ∈ Δ + ( i ) x i j k ) ≤ w i k ≤ b i ( ∑ j ∈ Δ + ( i ) x i j k ) ∀ k ∈ K , ∀ i ∈ N ( 6 ) E ≤ w i k ≤ L ∀ k ∈ K , ∀ i ∈ { 0 , n + 1 } ( 7 ) ∑ i ∈ N d i ∑ j ∈ Δ + ( i ) x i j k ≤ C ∀ k ∈ K ( 8 ) x i j k ≥ 0 ∀ k ∈ K , ∀ ( i , j ) ∈ A ( 9 ) x i j k binary ∀ k ∈ K , ∀ ( i , j ) ∈ A ( 10 ) \begin{array}{l} \min f(x)=1000 \sum_{k \in K} \sum_{j \in \Delta^{+}(0)} x_{0 j k}+\sum_{k \in K} \sum_{(i, j) \in A} c_{i j} x_{i j k} \\\\ \sum_{k \in K} \sum_{j \in \Delta^{+}(i)} x_{i j k}=1 \quad \forall i \in N \quad \quad \quad (1)\\ \sum_{j \in \Delta^{+}(0)} x_{0 j k}=1 \quad \forall k \in K \quad \quad \quad (2)\\ \sum_{i \in \Delta-(j)} x_{i j k}-\sum_{i \in \Delta^{+}(j)} x_{j i k}=0 \quad \forall k \in K, \forall j \in N \quad \quad \quad (3)\\ \sum_{i \in \Delta \Delta^{-(n+1)}} x_{i, n+1, k}=1 \quad \forall k \in K\quad \quad \quad (4) \\ w_{i k}+s_{i}+t_{i j}-w_{j k} \leq\left(1-x_{i j k}\right) M_{i j}, \forall k \in K, \forall(i, j) \in A \quad \quad \quad (5)\\ a_{i}\left(\sum_{j \in \Delta^{+}(i)} x_{i j k}\right) \leq w_{i k} \leq b_{i}\left(\sum_{j \in \Delta^{+}(i)} x_{i j k}\right) \quad \forall k \in K, \forall i \in N \quad \quad \quad (6)\\ E \leq w_{i k} \leq L \quad \forall k \in K, \forall i \in\{0, n+1\} \quad \quad \quad (7)\\ \sum_{i \in N} d_{i} \sum_{j \in \Delta^{+}(i)} x_{i j k} \leq C \quad \forall k \in K \quad \quad \quad (8) \\ x_{i j k} \geq 0 \quad \forall k \in K, \forall(i, j) \in A\quad \quad \quad (9)\\ x_{i j k} \text { binary } \forall k \in K, \forall(i, j) \in A \quad \quad \quad (10)\\ \end{array} minf(x)=1000∑k∈K∑j∈Δ+(0)x0jk+∑k∈K∑(i,j)∈Acijxijk∑k∈K∑j∈Δ+(i)xijk=1∀i∈N(1)∑j∈Δ+(0)x0jk=1∀k∈K(2)∑i∈Δ−(j)xijk−∑i∈Δ+(j)xjik=0∀k∈K,∀j∈N(3)∑i∈ΔΔ−(n+1)xi,n+1,k=1∀k∈K(4)wik+si+tij−wjk≤(1−xijk)Mij,∀k∈K,∀(i,j)∈A(5)ai(∑j∈Δ+(i)xijk)≤wik≤bi(∑j∈Δ+(i)xijk)∀k∈K,∀i∈N(6)E≤wik≤L∀k∈K,∀i∈{0,n+1}(7)∑i∈Ndi∑j∈Δ+(i)xijk≤C∀k∈K(8)xijk≥0∀k∈K,∀(i,j)∈A(9)xijk binary ∀k∈K,∀(i,j)∈A(10)
式中,目标函数 f ( x ) f(x) f(x)为总成本=1000*车辆使用数目+所有车辆行驶总距离, N N N表示顾客集合,约束(1)限制每个顾客只能被分配到一条路径;约束(2)-(4)表示车辆k在路径上的流量限制;约束(5)~(7)表示时间窗约束;约束(8)表示载重量约束,约束(9)-(10)表示决策向量约束。
参考文献:
[1]何美玲,魏志秀,武晓晖等.基于改进蚁群算法求解带软时间窗的车辆路径问题[J].计算机集成制造系统,2023,29(03):1029-1039.
[2]李琳,刘士新,唐加福.改进的蚁群算法求解带时间窗的车辆路径问题[J].控制与策,2010,25(09):1379-1383.
1.2VRPTW数据集简介
本文选取数据集的详细信息如下表所示,其包含1个配送中心(序号0表示配送中心),25个顾客(序号1-25),且每个车辆载重量限制为200。(可以更换为其他数据集)

二、蜣螂优化算法DBO
蜣螂优化算法(Dung beetle optimizer,DBO)由Jiankai Xue和Bo Shen于2022年提出,该算法主要受蜣螂的滚球、跳舞、觅食、偷窃和繁殖行为的启发所得。蜣螂优化算法DBO原理详细介绍
![]()
DBO算法描述如下:
![]()
参考文献:Xue, J., Shen, B. Dung beetle optimizer: a new meta-heuristic algorithm for global optimization. J Supercomput (2022). https://doi.org/10.1007/s11227-022-04959-6
三、蜣螂优化算法DBO求解VRPTW
close all
clear
clc
SearchAgents_no=50; % 种群大小
Function_name='F1';
Max_iteration=100; % 最大迭代次数
[lb,ub,dim,fobj]=Get_Functions_details(Function_name);
[fMin,bestX,curve]=DBO(SearchAgents_no,Max_iteration,lb,ub,dim,fobj); %算法求解
%% 显示最终结果
Pos=ShowResult(bestX);
%% 画图
figure
plot(curve,'Color','g','linewidth',1.5)%semilogy
xlabel('迭代次数');
ylabel('路径成本');
grid on
box on
legend('DBO')
%% 保存数据
save curve curve
save bestX bestX
配送路线1:0->21->6->0 服务顾客数量:2 路径长度:51.56878 装载量:14
服务顾客21的起始时间:18.02776,结束时间:28.02776
服务顾客6的起始时间:50.38844,结束时间:60.38844
抵达配送中心的时间:71.56878
配送路线2:0->12->22->1->0 服务顾客数量:3 路径长度:94.93124 装载量:47
服务顾客12的起始时间:15.00000,结束时间:25.00000
服务顾客22的起始时间:50.49510,结束时间:60.49510
服务顾客1的起始时间:99.69969,结束时间:109.69969
抵达配送中心的时间:124.93124
配送路线3:0->5->16->17->0 服务顾客数量:3 路径长度:73.39002 装载量:47
服务顾客5的起始时间:20.61553,结束时间:30.61553
服务顾客16的起始时间:41.79587,结束时间:51.79587
服务顾客17的起始时间:62.97621,结束时间:72.97621
抵达配送中心的时间:103.39002
配送路线4:0->2->3->4->0 服务顾客数量:3 路径长度:102.40930 装载量:39
服务顾客2的起始时间:18.00000,结束时间:28.00000
服务顾客3的起始时间:62.40930,结束时间:72.40930
服务顾客4的起始时间:97.40930,结束时间:107.40930
抵达配送中心的时间:132.40930
配送路线5:0->7->8->0 服务顾客数量:2 路径长度:59.66857 装载量:14
服务顾客7的起始时间:21.21320,结束时间:31.21320
服务顾客8的起始时间:43.41976,结束时间:53.41976
抵达配送中心的时间:79.66857
配送路线6:0->9->10->0 服务顾客数量:2 路径长度:82.51072 装载量:32
服务顾客9的起始时间:32.01562,结束时间:42.01562
服务顾客10的起始时间:67.01562,结束时间:77.01562
抵达配送中心的时间:102.51072
配送路线7:0->11->13->0 服务顾客数量:2 路径长度:85.95242 装载量:35
服务顾客11的起始时间:33.54102,结束时间:43.54102
服务顾客13的起始时间:84.77208,结束时间:94.77208
抵达配送中心的时间:105.95242
配送路线8:0->14->15->0 服务顾客数量:2 路径长度:78.24082 装载量:28
服务顾客14的起始时间:32.01562,结束时间:42.01562
服务顾客15的起始时间:57.82701,结束时间:67.82701
抵达配送中心的时间:98.24082
配送路线9:0->18->0 服务顾客数量:1 路径长度:31.62278 装载量:12
服务顾客18的起始时间:15.81139,结束时间:25.81139
抵达配送中心的时间:41.62278
配送路线10:0->19->20->0 服务顾客数量:2 路径长度:94.05221 装载量:26
服务顾客19的起始时间:32.01562,结束时间:42.01562
服务顾客20的起始时间:72.42943,结束时间:82.42943
抵达配送中心的时间:114.05221
配送路线11:0->23->24->25->0 服务顾客数量:3 路径长度:116.21931 装载量:38
服务顾客23的起始时间:36.05551,结束时间:46.05551
服务顾客24的起始时间:77.67829,结束时间:87.67829
服务顾客25的起始时间:102.67829,结束时间:112.67829
抵达配送中心的时间:146.21931
配送路线总长度:870.56615