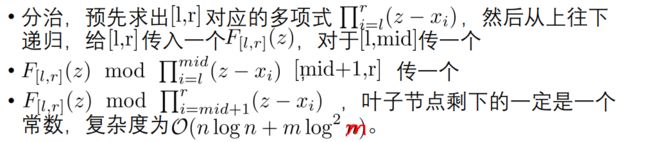多项式运算
多项式求逆
已知 f ( x ) f(x) f(x),求 g ( x ) g(x) g(x)满足 f ( x ) g ( x ) ≡ 1 ( m o d x n ) f(x)g(x)\equiv 1\pmod{x^n} f(x)g(x)≡1(modxn)。
若 f 0 = 0 f_0=0 f0=0,那么显然不可能存在形式幂级数 g ( x ) g(x) g(x)满足条件。于是假定 f 0 ≠ 0 f_0\neq 0 f0=0。
首先有 f ( x ) ≡ f 0 ( m o d x ) f(x)\equiv f_0\pmod {x} f(x)≡f0(modx),所以 g ( x ) ≡ f 0 − 1 ( m o d x ) g(x)\equiv f_0^{-1} \pmod {x} g(x)≡f0−1(modx)
假设已经求出了 f ( x ) g ′ ( x ) ≡ 1 ( m o d x n 2 ) f(x)g'(x)\equiv 1\pmod {x^\frac n2} f(x)g′(x)≡1(modx2n)
那么 f ( x ) g ′ ( x ) − 1 ≡ 0 ( m o d x n 2 ) f(x)g'(x)-1\equiv0\pmod {x^\frac n2} f(x)g′(x)−1≡0(modx2n)
两边平方使得模的次数翻倍(证明略): f 2 ( x ) g ′ 2 ( x ) − 2 f ( x ) g ′ ( x ) + 1 ≡ 0 ( m o d x n ) f^2(x)g'^2(x)-2f(x)g'(x)+1\equiv 0\pmod {x^n} f2(x)g′2(x)−2f(x)g′(x)+1≡0(modxn)
那么 f ( x ) ( 2 g ′ ( x ) − f ( x ) g ′ 2 ( x ) ) ≡ 1 ( m o d x n ) f(x)\left(2g'(x)-f(x)g'^2(x)\right)\equiv 1\pmod {x^n} f(x)(2g′(x)−f(x)g′2(x))≡1(modxn)
容易发现括号中的式子就是要求的 g ( x ) g(x) g(x),即 g ( x ) = 2 g ′ ( x ) − f ( x ) g ′ 2 ( x ) ( m o d x n ) g(x)=2g'(x)-f(x)g'^2(x) \pmod {x^n} g(x)=2g′(x)−f(x)g′2(x)(modxn)
前置知识:多项式牛顿迭代
用于寻找多项式零点,已知多项式 G G G,求满足 G ( F ( x ) ) ≡ 0 ( m o d x n ) G(F(x))\equiv0\pmod {x^n} G(F(x))≡0(modxn)的 F ( x ) F(x) F(x)
假设已经求出了 G ( F 0 ( x ) ) ≡ 0 ( m o d x n 2 ) G(F_0(x))\equiv0\pmod {x^{\frac n2}} G(F0(x))≡0(modx2n)
将 G ( F ( x ) ) G(F(x)) G(F(x))在 F 0 ( x ) F_0(x) F0(x)处泰勒展开:
G ( F ( x ) ) = ∑ n = 0 ∞ G ( n ) ( F 0 ( x ) ) n ! ( F ( x ) − F 0 ( x ) ) n G(F(x))=\sum_{n=0}^\infty{G^{(n)}(F_0(x))\over n!}(F(x)-F_0(x))^n G(F(x))=n=0∑∞n!G(n)(F0(x))(F(x)−F0(x))n
因为 F ( x ) − F 0 ( x ) ≡ 0 ( m o d x n 2 ) F(x)-F_0(x)\equiv 0\pmod {x^{\frac n2}} F(x)−F0(x)≡0(modx2n),所以展开式中在模 x n x^n xn意义下只需保留前两项:
G ( F ( x ) ) ≡ G ( F 0 ( x ) ) + G ′ ( F 0 ( x ) ) 1 ! ( F ( x ) − F 0 ( x ) ) ( m o d x n ) G(F(x))\equiv G(F_0(x))+{G'(F_0(x))\over 1!}(F(x)-F_0(x))\pmod {x^n} G(F(x))≡G(F0(x))+1!G′(F0(x))(F(x)−F0(x))(modxn)
而 G ( F ( x ) ) ≡ 0 ( m o d x n ) G(F(x))\equiv 0\pmod {x^n} G(F(x))≡0(modxn),代入后移项即得: F ( x ) = F 0 ( x ) − G ( F 0 ( x ) ) G ′ ( F 0 ( x ) ) ( m o d x n ) F(x)=F_0(x)-{G(F_0(x))\over G'(F_0(x))}\pmod {x^n} F(x)=F0(x)−G′(F0(x))G(F0(x))(modxn)
牛顿迭代多项式求逆
G ( x ) = 1 x − f ( z ) = 0 G(x)=\frac 1x-f(z)=0 G(x)=x1−f(z)=0 就可以牛顿迭代了。 x x x 是多项式。
x 1 = x 0 − 1 x 0 − f ( z ) − 1 x 0 2 = x 0 ( 2 − x 0 f ( z ) ) x_1=x_0-\frac {\frac 1{x_0}-f(z)}{-\frac 1{x_0^2}}=x_0(2-x_0f(z)) x1=x0−−x021x01−f(z)=x0(2−x0f(z))
多项式开根
已知 f ( x ) f(x) f(x),求 g ( x ) g(x) g(x)满足 g ( x ) 2 = f ( x ) ( m o d x n ) g(x)^2=f(x)\pmod {x^n} g(x)2=f(x)(modxn)
设 G ( x ) = x 2 − f G(x)=x^2-f G(x)=x2−f,牛顿迭代得到:
g 1 = g 0 − g 0 2 − f 2 g 0 = g 0 2 + f 2 g 0 g_1=g_0-{g_0^2-f\over 2g_0}={g_0\over2}+\frac f{2g_0} g1=g0−2g0g02−f=2g0+2g0f
Code(CF438E The Child and Binary Tree,题解):
#include多项式对数函数 ( ln ) (\ln) (ln)
已知 f ( x ) f(x) f(x),求 g ( x ) = ln f ( x ) ( m o d x n ) g(x)=\ln f(x)\pmod {x^n} g(x)=lnf(x)(modxn)
两边同时取导: g ′ ( x ) = f ′ ( x ) f ( x ) g'(x)={f'(x)\over f(x)} g′(x)=f(x)f′(x),再积分: g ( x ) = ∫ f ′ ( x ) f ( x ) g(x)=\int {f'(x)\over f(x)} g(x)=∫f(x)f′(x)
注意,因为积分舍去了常数项,所以这里的积分在 g 0 = 0 g_0=0 g0=0 的情况下才是对的,即 f 0 f_0 f0 必须等于 1 1 1
( l n x ln~x ln x 泰勒展开在模 x n x^n xn 意义下可以表示为 n − 1 n-1 n−1 次多项式,而 l n C ln~C ln C 没法表示)
Code:
void LN(int *A,int *B,int n){
INV(A,B,n); static int a[maxn]; int L=1<<(lg[n-2+n-1]+1);
rep(i,0,L-1) a[i]=i<n-1?1ll*A[i+1]*(i+1)%mod:0,i>=n&&(B[i]=0);
NTT(a,L,1),NTT(B,L,1); rep(i,0,L-1) a[i]=1ll*a[i]*B[i]%mod; NTT(a,L,-1);
rep(i,0,L-1) B[i]=i&&i<n?1ll*a[i-1]*inv[i]%mod:0;
}
多项式指数函数 ( exp ) (\exp) (exp)
已知 f ( x ) f(x) f(x),求 g ( x ) = e f ( x ) ( m o d x n ) g(x)=e^{f(x)}\pmod {x^n} g(x)=ef(x)(modxn)
ln g ( x ) = f ( x ) \ln g(x)=f(x) lng(x)=f(x),设 G ( x ) = ln x − f G(x)=\ln x-f G(x)=lnx−f,牛顿迭代:
g 1 = g 0 − ln g 0 − f 1 g 0 = g 0 ( 1 − ln g 0 + f ) g_1=g_0-\frac {\ln g_0-f}{\frac 1{g_0}}=g_0(1-\ln g_0+f) g1=g0−g01lng0−f=g0(1−lng0+f)
注意这里的 1 是常数而不是多项式。
需要保证 f 0 = 0 f_0=0 f0=0,才能保证 g ( x ) 0 = 1 g(x)_0=1 g(x)0=1,才可以求 ln \ln ln
Code:
void EXP(int *A,int *B,int n){
B[B[1]=0]=1; static int b[maxn];
for(int k=2,L=4;k<n<<1;k=L,L<<=1){
LN(B,b,k); rep(i,0,L-1) b[i]=i<k?upd((i==0)-b[i]+A[i]):(B[i]=0);
NTT(B,L,1),NTT(b,L,1); rep(i,0,L-1) B[i]=1ll*B[i]*b[i]%mod; NTT(B,L,-1); Clear(B,min(n,k),L-1);
}
}
分治FFT的做法 O ( n log 2 n ) O(n\log^2n) O(nlog2n)(比如这个提交):
g ( x ) = e f ( x ) g ′ ( x ) = e f ( x ) f ′ ( x ) = g ( x ) f ′ ( x ) ( n + 1 ) g n + 1 = ∑ i = 0 n ( i + 1 ) f i + 1 g n − i n g n = ∑ i = 1 n i f i g n − i = ∑ i = 0 n − 1 g i ∗ ( n − i ) f n − i ( n > 0 ) g 0 = e f 0 g(x)=e^{f(x)}\\ g'(x)=e^{f(x)}f'(x)=g(x)f'(x)\\ (n+1)g_{n+1}=\sum_{i=0}^n(i+1)f_{i+1}g_{n-i}\\ ng_n=\sum_{i=1}^nif_ig_{n-i}=\sum_{i=0}^{n-1}g_i*(n-i)f_{n-i}~~~~(n>0)\\ g_0=e^{f_0} g(x)=ef(x)g′(x)=ef(x)f′(x)=g(x)f′(x)(n+1)gn+1=∑i=0n(i+1)fi+1gn−ingn=∑i=1nifign−i=∑i=0n−1gi∗(n−i)fn−i (n>0)g0=ef0
EGF 经典应用:连通图计数
所有图的 EGF 为 G ( x ) = ∑ i ≥ 0 g i i ! x i G(x)=\sum_{i\ge 0} \frac {g_i}{i!}x^i G(x)=∑i≥0i!gixi
连通图的 EGF 为 F ( x ) = ∑ i ≥ 1 f i i ! x i F(x)=\sum_{i\ge 1} \frac {f_i}{i!}x^i F(x)=∑i≥1i!fixi
那么有 G ( x ) = e F ( x ) = ∑ i ≥ 0 F ( x ) i i ! G(x)=e^{F(x)}=\sum_{i\ge 0}\frac {F(x)^i}{i!} G(x)=eF(x)=∑i≥0i!F(x)i
可以最后得到 g n g_n gn 需要乘上 n ! n! n! 。可以理解为枚举连通块个数,然后分配标号,连通块内部无序,每种有 k k k 个连通块的方案都被算了 k ! k! k! 次。
多项式快速幂
已知 f ( x ) f(x) f(x),求 g ( x ) = f ( x ) k ( m o d x n ) g(x)=f(x)^k\pmod {x^n} g(x)=f(x)k(modxn)
-
k ≤ 1 0 9 k\le10^9 k≤109
倍增,为了避免循环卷积每次点值相乘后都要IDFT。 O ( n log n log k ) O(n\log n\log k) O(nlognlogk) -
O ( δ ( f ) ∗ k ) O(\delta(f)*k) O(δ(f)∗k), δ ( f ) \delta(f) δ(f) 表示 f ( x ) f(x) f(x) 的最高次数
同样倍增,但是只要FFT的长度大于等于 δ ( f ) ∗ k \delta(f)*k δ(f)∗k,就不需要每次IDFT了,直接对点值快速幂即可。 -
O ( δ ( f ) ∗ n ) O(\delta(f)*n) O(δ(f)∗n)
求导可得 g ′ ( x ) = k f ( x ) k − 1 f ′ ( x ) ⟹ g ′ ( x ) f ( x ) = k f ′ ( x ) g ( x ) g'(x)=kf(x)^{k-1}f'(x)\Longrightarrow g'(x)f(x)=kf'(x)g(x) g′(x)=kf(x)k−1f′(x)⟹g′(x)f(x)=kf′(x)g(x)
对第 t t t 项展开可得 ∑ i = 0 t ( t − i + 1 ) f i g t − i + 1 = ∑ i = 0 t k ( i + 1 ) f i + 1 g t − i \sum_{i=0}^t(t-i+1)f_ig_{t-i+1}=\sum_{i=0}^tk(i+1)f_{i+1}g_{t-i} ∑i=0t(t−i+1)figt−i+1=∑i=0tk(i+1)fi+1gt−i
所以 g t + 1 ( t + 1 ) f 0 = ∑ i = 1 t k i f i g t − i + 1 − ( t − i + 1 ) f i g t − i + 1 = ∑ i = 1 t f i g t − i + 1 ( ( k + 1 ) i − t − 1 ) g_{t+1}(t+1)f_0=\sum_{i=1}^tkif_ig_{t-i+1}-(t-i+1)f_ig_{t-i+1}=\sum_{i=1}^tf_ig_{t-i+1}((k+1)i-t-1) gt+1(t+1)f0=∑i=1tkifigt−i+1−(t−i+1)figt−i+1=∑i=1tfigt−i+1((k+1)i−t−1)
于是可以 O ( δ ( f ) ) O(\delta (f)) O(δ(f)) 递推出答案的下一项。 -
k ≤ 1 0 1 0 5 k\le10^{10^5} k≤10105
考虑 f ( x ) k = exp ( k ln f ( x ) ) f(x)^k=\exp(k\ln f(x)) f(x)k=exp(klnf(x))
而在 m o d 998244353 \bmod~{998244353} mod 998244353 意义下 k ln f ( x ) ≡ ( k m o d 998244353 ) ln f ( x ) k\ln f(x)\equiv(k\bmod998244353)\ln f(x) klnf(x)≡(kmod998244353)lnf(x)
所以可以在输入的时候就将 k m o d 998244353 k\bmod998244353 kmod998244353
然后就可以使用第一种做法了。
注意在模小质数意义下是不能这么解的,因为当 δ ( f ) > m o d \delta(f)>mod δ(f)>mod的时候 ln f ( x ) \ln f(x) lnf(x) 可能没有意义 -
exp 做 法 \exp做法 exp做法
如果保证 f ( x ) [ x 0 ] = 1 f(x)[x^0]=1 f(x)[x0]=1,那么可以直接 ln \ln ln 乘 k k k 然后 exp \exp exp, O ( n log n ) O(n\log n) O(nlogn)
常数项不为1没法求 ln \ln ln,那就先除掉嘛, f ( x ) k = ( f ( x ) f 0 ) k ∗ f 0 k f(x)^k=\left(\frac {f(x)}{f_0}\right)^k*f_0^k f(x)k=(f0f(x))k∗f0k,然后括号里面就可以直接做了。
但是 f 0 f_0 f0可能等于 0,于是找到最低次不为0的项 a t x t a_tx^t atxt,得到:
f ( x ) k = ( f ( x ) a t x t ) k ∗ a t k x t k f(x)^k=\left(\frac {f(x)}{a_tx^t}\right)^k*a_t^kx^{tk} f(x)k=(atxtf(x))k∗atkxtk括号里面的式子在 ( m o d x n − t k ) \pmod {x^{n-tk}} (modxn−tk) 意义下算就可以了。
多项式取模
暴力大除法 A ( x ) m o d B ( x ) A(x) \bmod B(x) A(x)modB(x) ,复杂度 O ( d e g ( B ) ∗ ( d e g ( A ) − d e g ( B ) ) ) O(deg(B)*(deg(A)-deg(B))) O(deg(B)∗(deg(A)−deg(B)))
暴力求 g c d ( A ( x ) , B ( x ) ) gcd(A(x),B(x)) gcd(A(x),B(x)) 的首一多项式的复杂度是 O ( d e g ( A ) ∗ d e g ( B ) ) O(deg(A)*deg(B)) O(deg(A)∗deg(B)) 的。 T ( n , m ) = m ∗ ( n − m ) + O ( m 2 ) = O ( n m ) T(n,m)=m*(n-m)+O(m^2)=O(nm) T(n,m)=m∗(n−m)+O(m2)=O(nm)
多项式多点求值
方法一:分治取模
![]()
基本思路1: F ( x i ) = F ( z ) m o d ( z − x i ) F(x_i)=F(z) \bmod (z-x_i) F(xi)=F(z)mod(z−xi)
因为 z m o d ( z − x i ) = x i z \bmod (z-x_i)=x_i zmod(z−xi)=xi,或令 F ( z ) = A ( z ) ( z − x i ) + B ( z ) F(z)=A(z)(z-x_i)+B(z) F(z)=A(z)(z−xi)+B(z),带入 z = x i z=x_i z=xi 。
基本思路2: ( F ( z ) m o d A ( z ) B ( z ) ) m o d B ( z ) = F ( z ) m o d B ( z ) (F(z) \bmod A(z)B(z))\bmod B(z)=F(z)\bmod B(z) (F(z)modA(z)B(z))modB(z)=F(z)modB(z)
解法:
先令 F [ 1 , m ] = F ( z ) m o d ∏ 1 ≤ i ≤ m ( z − x i ) F_{[1,m]}=F(z)\bmod \prod_{1\le i\le m} (z-x_i) F[1,m]=F(z)mod∏1≤i≤m(z−xi),然后分治:
然而取模需要一次求逆,两次乘法,导致这个做法很慢。(没试过不知道,大家都说慢)
类似的做法可以解决 ∏ 1 ≤ j < i ≤ n ( a i − a j ) \prod_{1\le j
记 F i ( z ) = ∏ 1 ≤ j < i ( z − a j ) F_i(z)=\prod_{1\le j
分治 F [ l , r ] = ∏ 1 ≤ j < l ( z − a j ) m o d ∏ l ≤ i ≤ r ( z − a i ) F_{[l,r]}=\prod_{1\le j
传进左边的时候模上 ∏ l ≤ i ≤ m i d ( z − a i ) \prod_{l\le i\le mid}(z-a_i) ∏l≤i≤mid(z−ai)
传进右边的多项式是 F [ l , r ] ∗ ∏ l ≤ j ≤ m i d ( z − a j ) m o d ∏ m i d + 1 ≤ i ≤ r ( z − a i ) F_{[l,r]}*\prod_{l\le j\le mid}(z-a_j) \bmod \prod_{mid+1\le i\le r}(z-a_i) F[l,r]∗∏l≤j≤mid(z−aj)mod∏mid+1≤i≤r(z−ai)
传到叶子的时候显然就是 F i ( z ) m o d ( z − a i ) F_i(z)\bmod (z-a_i) Fi(z)mod(z−ai)
方法二:分治减法卷积
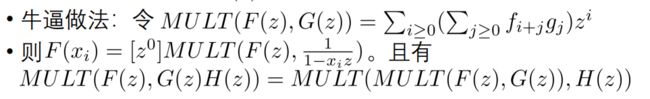
M U L T MULT MULT 即减法卷积(差为定值),第三行的性质是因为 i − ( j + k ) = i − j − k i-(j+k)=i-j-k i−(j+k)=i−j−k
令 F [ l , r ] = M U L T ( F ( z ) , ∏ l ≤ i ≤ r 1 1 − x i z ) F_{[l,r]}=MULT(F(z),\prod_{l\le i\le r}\frac 1{1-x_iz}) F[l,r]=MULT(F(z),∏l≤i≤r1−xiz1)
那么 F [ l , m i d ] = M U L T ( F ( z ) , ∏ l ≤ i ≤ r 1 1 − x i z ∗ ∏ m i d + 1 ≤ i ≤ r ( 1 − x i z ) ) = M U L T ( F [ l , r ] , ∏ m i d + 1 ≤ i ≤ r ( 1 − x i z ) ) F_{[l,mid]}=MULT(F(z),\prod_{l\le i\le r}\frac 1{1-x_iz}*\prod _{mid+1\le i\le r}(1-x_iz))=MULT(F_{[l,r]},\prod_{mid+1\le i\le r}(1-x_iz)) F[l,mid]=MULT(F(z),∏l≤i≤r1−xiz1∗∏mid+1≤i≤r(1−xiz))=MULT(F[l,r],∏mid+1≤i≤r(1−xiz))
右边类似, F [ m i d + 1 , r ] = M U L T ( F [ l , r ] , ∏ l ≤ i ≤ m i d ( 1 − x i z ) ) F_{[mid+1,r]}=MULT(F_{[l,r]},\prod_{l\le i\le mid}(1-x_iz)) F[mid+1,r]=MULT(F[l,r],∏l≤i≤mid(1−xiz))
每层最高项只需要保留到区间长度,因为大于区间长度的项最后对 [ z 0 ] [z^0] [z0] 没有贡献。
与方法一一样,先从下到上做一次分治FTT预处理,在根部做一次求逆和减法卷积,然后从上往下分治。每层只需要做减法卷积(一次乘法),比取模快很多。
多项式多点插值

相当于 F ( z ) = ∑ i = 0 n a i ∏ j ≠ i z − x j F(z)=\sum_{i=0}^na_i\prod_{j\neq i}z-x_j F(z)=∑i=0nai∏j=iz−xj,从下到上分治,每次乘上左边或右边的 ∏ z − x j \prod z-x_j ∏z−xj 即可。
那么问题就是如何算 ∏ j ≠ i x i − x j \prod_{j\neq i}x_i-x_j ∏j=ixi−xj
令 G ( z ) = ∏ i = 0 n ( z − x i ) G(z)=\prod_{i=0}^n(z-x_i) G(z)=∏i=0n(z−xi),那么 G ( z ) ′ = ∑ i ∏ j ≠ i ( x − x j ) G(z)'=\sum_i\prod_{j\neq i}(x-x_j) G(z)′=∑i∏j=i(x−xj), G ( x i ) ′ = ∏ j ≠ i ( x − x j ) G(x_i)'=\prod_{j\neq i}(x-x_j) G(xi)′=∏j=i(x−xj)
分治求出 G ( z ) G(z) G(z),求导之后多点求值即可。 G ( z ) ′ G(z)' G(z)′ 这里可以用洛必达化成 ∏ x − x j x − x i \frac {\prod x-x_j}{x-x_i} x−xi∏x−xj 在 x = x i x=x_i x=xi 处的取值来理解,不过既不明所以又没有必要。
多项式复合
多项式复合逆
因为函数/多项式复合满足结合律。求的是 F F F 的左逆,假设 F ( H ( z ) ) = z F(H(z))=z F(H(z))=z,那么有:
G ( z ) = G ( F ( H ( z ) ) ) = ( G ∘ F ) ( H ( z ) ) = H ( z ) G(z)=G(F(H(z)))=(G\circ F)(H(z))=H(z) G(z)=G(F(H(z)))=(G∘F)(H(z))=H(z)
拉格朗日反演
为了与PPT统一(懒得改),以下 x x x 均表示关于 z z z 的多项式,即 x ( z ) x(z) x(z)
若 F ( z ) 与 x ( z ) 互 为 复 合 逆 , 即 F 和 x 的 常 数 项 为 0 , 1 次 项 非 0 , 且 F ( x ) = z , 则 : [ z n ] x = 1 n [ z − 1 ] ( 1 F ( z ) ) n 若 F(z) 与 x(z) 互为复合逆,即 F 和 x 的常数项为0,1次项非0,且F(x)=z,则:\\ [z^n]x=\frac 1n[z^{-1}](\frac 1{F(z)})^n 若F(z)与x(z)互为复合逆,即F和x的常数项为0,1次项非0,且F(x)=z,则:[zn]x=n1[z−1](F(z)1)n
取 z − 1 z^{-1} z−1 是因为这里的多项式的域是分式环,即 A ( z ) B ( z ) \frac {A(z)}{B(z)} B(z)A(z),不需要考虑 B ( z ) B(z) B(z) 是否可逆,因为可以把它表示为 z d ∗ B ′ ( z ) z^d*B'(z) zd∗B′(z),它的逆就是 z − d ∗ 1 B ′ ( z ) z^{-d}*\frac 1{B'(z)} z−d∗B′(z)1 ,所以任何多项式都可逆。
更实用的形式是 [ z n ] x = 1 n [ z n − 1 ] ( z F ( z ) ) n [z^n]x=\frac 1n[z^{n-1}](\frac z{F(z)})^n [zn]x=n1[zn−1](F(z)z)n,因为 F ( z ) F(z) F(z) 常数项为 0,所以就可以在普通的形式幂级数下求逆和快速幂了。
扩展形式: [ z n ] H ( x ) = 1 n [ z − 1 ] H ′ ( z ) ( 1 F ( z ) ) n [z^n]H(x)=\frac 1n[z^{-1}]H'(z)(\frac 1{F(z)})^n [zn]H(x)=n1[z−1]H′(z)(F(z)1)n
于是求复合逆单项可以 O ( n log n ) O(n\log n) O(nlogn)
证明
听完课后不到10min就看懂了网上那篇以前看起来是天书的拉格朗日反演blog…
myh赛高!
简单应用
特殊应用:二元生成函数
考虑二元生成函数 H ( u , z ) = 1 1 − u z H(u,z)=\frac 1{1-uz} H(u,z)=1−uz1
那么由扩展拉格朗日反演有: [ z n ] H ( u , F ( z ) ) = 1 n [ z n − 1 ] H ( u , z ) ′ ( z F − 1 ( z ) ) n [z^n]H(u,F(z))=\frac 1n[z^{n-1}]H(u,z)'(\frac z{F^{-1}(z)})^n [zn]H(u,F(z))=n1[zn−1]H(u,z)′(F−1(z)z)n,其中 F − 1 ( z ) F^{-1}(z) F−1(z) 是 F ( z ) F(z) F(z) 的复合逆。
[ z n ] 1 1 − u F ( z ) = 1 n [ z n − 1 ] ( 1 1 − u z ) ′ ( z F − 1 ( z ) ) n [z^n]\frac 1{1-uF(z)}=\frac 1n[z^{n-1}](\frac 1{1-uz})'(\frac z{F^{-1}(z)})^n [zn]1−uF(z)1=n1[zn−1](1−uz1)′(F−1(z)z)n
而 d ( 1 1 − u z ) d z = ∑ i ≥ 0 u i + 1 ( i + 1 ) z i \frac {d(\frac 1{1-uz})}{dz}=\sum_{i\ge 0}u^{i+1}(i+1)z^i dzd(1−uz1)=∑i≥0ui+1(i+1)zi
也就是说在求出 ( z F − 1 ( z ) ) n (\frac z{F^{-1}(z)})^n (F−1(z)z)n 后,可以 O ( n ) O(n) O(n) 算出右边 i ∈ [ 0 , n ] , [ u i ] i\in[0,n],[u^i] i∈[0,n],[ui] 的值。
而左边等于 ∑ i ≥ 0 [ z n ] F ( z ) i u i \sum_{i\ge 0}[z^n]F(z)^iu^i ∑i≥0[zn]F(z)iui,于是我们就得到了 i ∈ ( 0 , n ] , [ z n ] F ( z ) i i\in(0,n],[z^n]F(z)^i i∈(0,n],[zn]F(z)i 的值。
当 F ( z ) F(z) F(z) 没有复合逆时,有两种情况:
(1) [ z 0 ] F ( z ) = c [z^0]F(z)=c [z0]F(z)=c,则令 P ( z ) = F ( z ) − c P(z)=F(z)-c P(z)=F(z)−c,求出 [ z n ] P ( z ) i [z^n]P(z)^i [zn]P(z)i 之后二项式定理展开 ( P ( z ) + c ) i (P(z)+c)^i (P(z)+c)i
做一次卷积即可。
(2) F ( z ) F(z) F(z) 的最低次项 k ≥ 2 k\ge 2 k≥2,则令 P ( z ) = F ( z ) 1 k P(z)=F(z)^{\frac 1k} P(z)=F(z)k1,那么 F ( z ) i = P ( z ) k i F(z)^i=P(z)^{ki} F(z)i=P(z)ki,而 [ z n ] F ( z ) i [z^n]F(z)^i [zn]F(z)i 只有当 i ≤ n k i\le \frac nk i≤kn 时有值。
二元生成函数 H ( u , z ) H(u,z) H(u,z) 的 u u u 的指数 u i u^i ui 表示选了 i i i 个 F F F 乘起来。 z z z 的指数在具体的题目中也可以体现不同的含义。
例题:ZJOI2020 抽卡