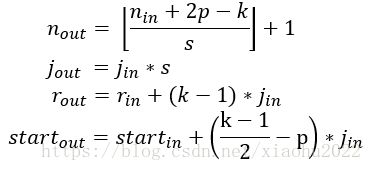卷积神经网络的感受野（一）

本文将参考多个教程来学习记录：

如何计算卷积神经网络（CNN） 的感受野？

你知道如何计算CNN感受野吗？这里有一份详细指南 - 知乎

卷积神经网络之CNN感受野计算_专注于计算机视觉的AndyJiang的博客-CSDN博客_卷积神经网络感受野计算公式

一、前言

感受野是CNN中的基础概念之一。那么什么是感受野？感受野在CNN中是如何计算的？

深入理解感受野对于一些任务的网络结构设计和优化有着重要意义，比如语义分割模型的空洞卷积，其中就涉及到对感受野的深刻理解。

这里默认大家都有CNN基本知识储备，对于卷积核和特征图等概念都有基本理解，熟悉CNN的计算原理。所以我们直接来切入正题，先来看如何给感受野一个明确的定义。

二、感受野

1）感受野(Receptive Field, RF)是指特征图上某一个像素对应到输入空间中的区域范围。所以感受野可以理解为特征图像素到输入区域的映射。

2）感受野指的是一个特定的CNN特征（特征图上的某个点）在输入空间所受影响的区域。一个感受野可以用中心位置和大小来表征。然而对于一个CNN特征来说，感受野中的每个像素值并不是同等重要的。越接近感受野中心的像素点，则它对输出特征的计算所起的作用越大。

先来回顾一个从输入到特征图的计算过程：

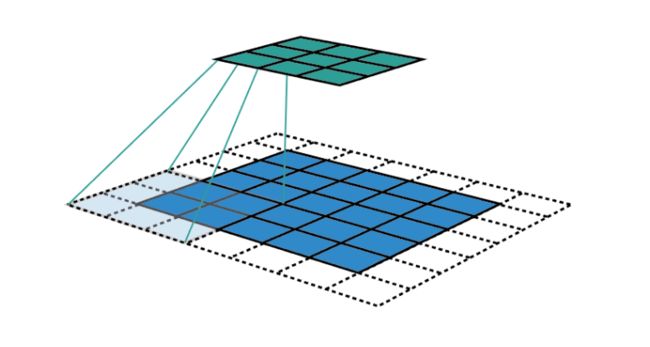
其中n_in为输入size，p为padding大小，f为卷积核size，s为卷积步长。假设输入大小为5*5，f=3*3，padding为1*1，卷积步长为2*2，那么输出特征图size根据公式可计算为3*3。如下图所示：

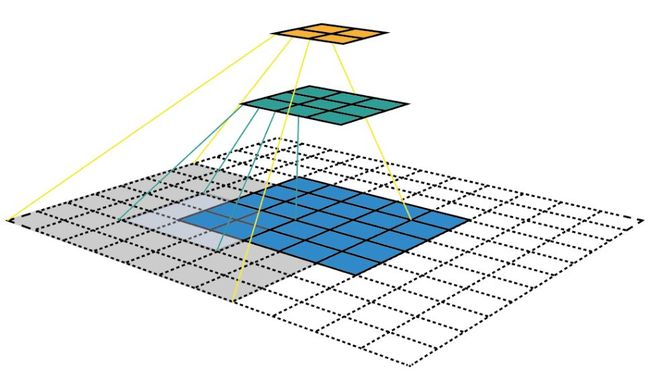
然后我们继续对3*3的特征图执行卷积，卷积参数同第一次卷积一样，可得输出特征图size为2*2。我们把输入、两次卷积过程和对应特征图放到一起看一下：

可以看到两次卷积的特征图分别对应到输入空间的感受野大小，第一次卷积对应关系如图中绿色线条所示，感受野大小为3*3，第二次卷积对应关系如图中黄色线条所示，感受野大小为7*7。所以关键问题是特征图和输入空间的对应关系中，感受野的大小是如何计算的？

下面我们给出感受野大小的计算公式：

 其中RF_l+1为当前特征图对应的感受野大小，也就是我们要计算的目标感受野，RF_l为上一层特征图对应的感受野大小，f_l+1为当前卷积层卷积核大小，最后一项连乘项则表示之前卷积层的步长乘积。

 根据感受野的计算公式我们来看上图中两次卷积的感受野计算过程：

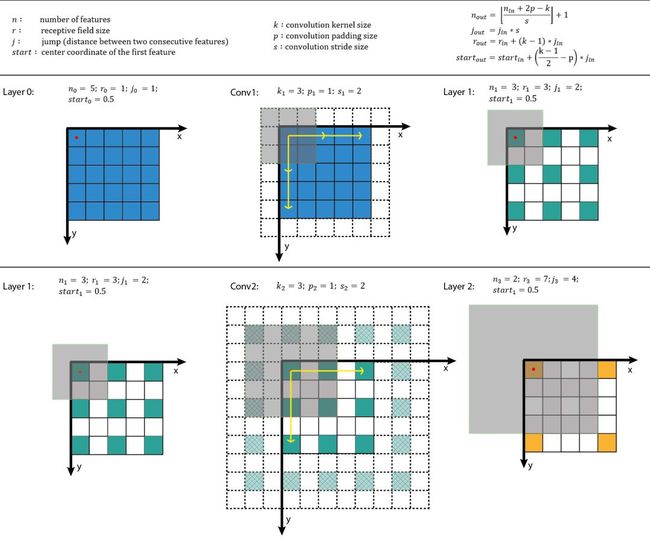
（1）原始输入size为5*5，第一层卷积核为3*3，输入步长为1，输入层初始化感受野为1*1，根据公式计算可得第一层卷积后的特征图对应的输入空间的感受野大小为1+(3-1)*1=3。

（2）第一层卷积输出特征图的感受野size为3，第二层卷积核size为3，卷积步长为2，则第二层的感受野size计算结果为：3 + （3-1） * （1*2） = 7。所以我们可以看到当前层特征图的感受野大小对应到输入空间与前层的感受野和卷积步长以及当前层的卷积核大小密切相关。当步长大于1时，感受野的大小会呈现指数级增长。

三、计算过程

上述计算的图示过程如下：

感受野还有一点比较重要的是，对于一个卷积特征图而言，感受野中每个像素并不是同等重要的，越接近感受野中间的像素相对而言就越重要。

深刻理解感受野的概念对于CNN结构设计意义重大，语义分割中很多网络结构的设计都会在感受野上做文章，比如说我们下一问会讲到的空洞卷积，以及后续的deeplab系列分割网络。

感受野计算公式

为了计算CNN每一层的感受野，除了要知道特征图每个维度的特征数，还需要记录每一层的其他信息：包括当前层的感受野大小，两个相邻特征的距离（跳跃的距离），和左上角特征（第一个特征）的中心坐标。

注意感受野（其实是特征图第一个特征的感受野）的中心坐标就等于这个特征的中心坐标，

当采用的卷积其核大小为，padding大小为，步长为，输出特征图的感受野可以按照如下公式计算：
 

 

第一个式子根据输入特征图大小以及卷积参数计算输出特征图大小，前面已经说过。

第二个式子计算输出特征图的特征间的间隔，其等于上一层的间隔值乘以卷积的步长，所以间隔值将是按照步长呈指数级增长。

第三个式子计算输出特征图的感受野大小，其等于前一层感受野大小加上，所以感受野是呈指数级增加，并且还有一个因子k−1。

第四个式子计算输出特征图的第一个特征感受野的中心坐标，其等于第一层的中心坐标加上(k−1)/2∗jin，再减去p∗jin，注意两项都要乘以前一层的间隔距离以得到实际距离。

注：对于第一层，一般是输入图片，其各项值为：n=image_size, r=1, j=1, start=0.5。

下图给出了一个如何计算感受野的实例，图中的坐标系统中，输入层的第一个特征中心位置记为0.5。通过利用上面公式迭代地进行计算，你可以计算出CNN中所有特征图的感受野信息。

注：layer0中的第一个特征（或叫特征点，特征图上的像素点）的这种中心位置就是那个第一个小蓝色格子的中心坐标红色小点点。那个j就是表示两个特征点之间的距离（比如layer0中两个相邻特征（点）之间的距离为1，在layer1中两个相邻特征之间的距离是2，在layer2中两个相邻特征之间的距离是4）

给出一个更简洁的计算公式，对于第k层的感受野大小计算如下：

                                     

其中是第k − 1层的感受野大小，而是当前层的卷积核大小，是第i层的步长(stride)。

从这个公式可以看到，相比前一层，当前层的感受野大小在两层之间增加了

如果stride大于1的话，这是一个指数级增加。

四、

在CNN中，感受野应该是一个很重要的东西，但是往往被大家忽略，图像分割模型DeepLab就提到了感受野大小的问题，但是那里并没有给出计算公式，如果采用上面的公式就可以快速得到结果。对于图像分割，感受野大小对分割效果是有很大影响的，所以DeepLab采用了扩展卷积或者空洞卷积（Atrous Convolution， Dilated Convolution）来增加感受野大小。对于空洞卷积来说，你可以将其转化为普通卷积（卷积核大小增加）来计算特征图的感受野。另外，上面的公式同样适用于池化层，因为其在结构上与卷积层是类似的。