Diagonalwise Refactorization: An Efficient Training Method for Depthwise Convolutions笔记
论文地址:Diagonalwise Refactorization: An Efficient Training Method for Depthwise Convolutions
##摘要
Depthwise Conv由于减少了参数和乘加运算因而具备显着的性能优势。然而,在当前的深度学习框架中,使用GPU进行Depthwise Conv训练的速度很慢,因为它们的实现不能充分利用GPU的能力。为了解决这个问题,本文提出了一种有效的方法(称为 对角线重构 )来加速Depthwise Conv层的训练。我们的主要想法是将Depthwise Conv的权重向量重新组合成一个大的对角权重矩阵,以便将Depthwise Conv转换为单个标准卷积,这一操作可以使用针对GPU计算高度优化的cuDNN库运行。我们在五个流行的深度学习框架中实施了我们的训练方法。评估结果表明,我们提出的方法相比于原始实现,在Darknet上获得 15.4 × 15.4\times 15.4×的训练加速,在Caffe上获得 8.4 × 8.4\times 8.4×的提升,在PyTorch上获得 5.4 × 5.4\times 5.4×的提升,在MXNet上获得 3.5 × 3.5\times 3.5×的提升,在TensorFlow上获得 1.4 × 1.4\times 1.4×的提升。
##引言
MobileNets使用深度可分离卷积,将一个标准卷积分解为深度卷积和逐点卷积( 1 × 1 1 \times 1 1×1),有效减少参数和乘加操作的数量。
Xception利用深度可分卷积来提高分类性能。但是,正如文献[9][10]所报告的那样,深度卷积具有较低的计算/存储器访问比,这意味着存储器访问比计算需要更多的执行时间,并且很难像标准卷积那样的计算密集型层一样高效执行。这使得在当前的深度学习框架(如Caffe、PyTorch、MXNet和TensorFlow)中使用GPU训练深度卷积层非常缓慢,主要是因为它们Depthwise Conv的实现不能充分利用GPU性能。
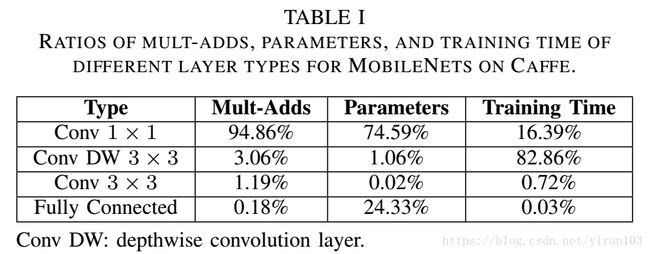
Caffe、PyTorch和MXNet通过在每个通道上执行标准卷积来实现深度卷积。此方法只是为每个输入通道启动CUDA内核或cuDNN函数,并且不应用通道间优化(如滤波器组合)。因此,为每个标准卷积启动的线程数量很少,并且GPU内核的利用率非常低。例如,尽管在训练MobileNets时,深度卷积只占乘加运算的约3%,参数的1%,他们的花费超过Caffe整体训练时间的82%,远高于其他层类型,如下表所示。
与逐通道方法不同,TensorFlow采用特殊内核方法实现深度卷积。该方法设计专门的CUDA内核,在单个kernel中计算所有输入通道。这种方法在深度卷积层训练中效率更高,因为它利用了通道间的并行性。但是,专门的内核方法导致TensorFlow无法利用cuDNN库带来的算法级别和微架构级别的优化,而这对于高性能GPU计算至关重要。
本文提出了对角线重构,一种有效加速深度卷积层训练的方法。首先,将输入通道的权重向量(滤波器)重新排列成对角矩阵,以构造一个单一的大滤波器。然后,深度卷积变为计算与大滤波器的标准卷积,其支持利用cuDNN库来加速计算。并且,在输入通道数量较多时,我们采用分组机制进行卷积——将通道分成若干组,并对每组进行对角线重构。通过将所有滤波器组合到一个较大的滤波器中,我们的方法可以利用通道间并行,更高效地调度GPU。通过支持cuDNN库,我们的方法可以直接享受其算法级和微架构级优化。
我们对不同超参数的MobileNet进行了广泛的实验,包括浅层模型、宽度乘数和分辨率乘数,并逐层对训练时间进行了详细分析。代码已在Github上公布(Caffe, Pytorch, Tensorflow)。
本文的贡献总结如下:
- 我们提出了一种有效加速深度卷积训练的新方法(对角重构)。
- 我们在五个流行的框架上实现我们的方法并提供详细的性能比较和分析。
- 我们讨论我们方法的可扩展性并表明它可以用于许多加速技术的训练如剪枝和组卷积。
##相关工作
深度可分卷积是深度卷积和逐点卷积的组合。如图所示,深度卷积滤波器(kernel)的权重仅应用于一个输入通道。对于 $ M $ 通道的输入特征映射,深度卷积创建 $ M $ 通道的输出特征映射。深度可分卷积显着减少了参数和乘加运算,从而有效地加速了卷积网络的计算。例如,MobileNets在移动设备上推理非常快[7][31][32]。我们基于YOLOv2检测框架,在i7 CPU(0.375-MobileNet-416模型1)和具备NEON加速的iMx6 ARM(0.375-MobileNet-128模型)上实现了实时单类检测。

目前深度卷积有两种实现(逐通道和专用内核),这两种方法都基于标准卷积。
标准卷积
假设输入和输出通道的数量分别是 $ M $ 和 $ N $,特征映射的大小是 $ F \times F $,并且卷积核的大小是 $ K \times K $ 。标准卷积分两步实现,如图所示。
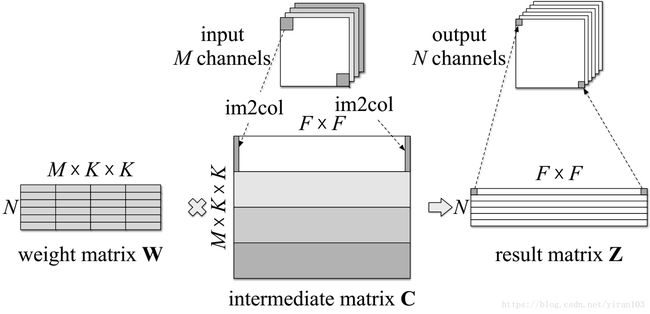
第一步是一个im2col操作,将输入特征映射 $ X_{M \times F \times F} $ 重排列成一个中间矩阵 C ( M ⋅ K ⋅ K ) × ( F ⋅ F ) {C}_{(M \cdot K \cdot K) \times (F \cdot F)} C(M⋅K⋅K)×(F⋅F) ,在 $ {X} $ 中进行卷积的每个块都重新排列成 ${C} $ 的列;
第二步是卷积权重 $ {W}_{N \times (M \cdot K \cdot K)}$ 与中间值矩阵 W N × ( M ⋅ K ⋅ K ) {W}_{N \times (M \cdot K \cdot K)} WN×(M⋅K⋅K) 的矩阵乘法。所得结果 Z N × ( F ⋅ F ) {Z}_{N \times (F \cdot F)} ZN×(F⋅F) 中每一行表示输出特征映射的一个通道。
逐通道方法
如图所示,该方法仅仅为每个输入通道执行标准卷积。

首先使用im2col操作生成 $ M $ 个中间矩阵 C ( K ⋅ K ) × ( F ⋅ F ) ( i ) {C}^{(i)}_{(K \cdot K) \times (F \cdot F)} C(K⋅K)×(F⋅F)(i) 。
然后,进行 $ M $ 次权重向量 w K × K ( i ) {w}^{(i)}_{K \times K} wK×K(i) 与 中间矩阵 C ( i ) {C}^{(i)} C(i) 的乘法。
最后,平铺 $ M $ 个结果向量 z F × F ( i ) {z}^{(i)}_{F \times F} zF×F(i) 生成结果矩阵 Z {Z} Z 。
Caffe、PyTorch和MXNet均采用逐通道法。此时,Caffe只支持利用通用矩阵乘法(GEMM)操作,不支持cuDNN,而PyTorch和MXNet支持使用cuDNN。如下表所示,与Caffe相比,二者具有明显的性能优势。

专用内核法
该方法没有明确生成中间矩阵 C {C} C ,并自行设计了专用CUDA内核来实现深度卷积,而不使用GEMM或cuDNN。在CUDA线程中, K × K K \times K K×K 输入特征图 X {X} X 中的一个 K × K K \times K K×K 块与对应权重 w ( i ) {w}^{(i)} w(i) 进行卷积,以计算输出特征图 Z {Z} Z 上的一个元素。TensorFlow中采用了专用内核法,其手动优化了GPU的共享内存和缓存。
##设计
在本节中,我们首先介绍对角线重构方法,然后描述大量输入通道的分组机制。最后,我们分析了我们的方法相比之前方案的优势。
###对角线重构
考虑 $ M $ 个输入通道的深度卷积。在正常的深度卷积中,单个滤波器是长度为 K × K K \times K K×K 的向量。卷积运算是权重向量 w K × K ( i ) {w}^{(i)}_{K \times K} wK×K(i) 与 对应通道中间矩阵 C ( i ) {C}^{(i)} C(i) 的乘法。深度卷积由 $ M $ 个向量矩阵乘法组成。如下图所示,在对角线重构中,我们将深度卷积转换为标准卷积。将$ M $ 个加权向量 w ( i ) {w}^{(i)} w(i) 放置于大权重矩阵 W M × ( M ⋅ K ⋅ K ) {W}_{M \times (M \cdot K \cdot K)} WM×(M⋅K⋅K) 的对角线位置,而所有其他位置设置为0。 im2col矩阵 C ( i ) {C}^{(i)} C(i) 从上到下平铺并形成一个大的中间矩阵 C ( M ⋅ K ⋅ K ) × ( F ⋅ F ) {C}_{(M \cdot K \cdot K) \times (F \cdot F)} C(M⋅K⋅K)×(F⋅F) ,这与在标准卷积中相同。在向后传播过程中,顶层的梯度只传递给对角线权重,其他所有位置都保持为0。
这一转换可以表示为在一个$ M $ 通道标准卷积之前进行权重矩阵 W {W} W 和常数掩码矩阵 A M × ( M ⋅ K ⋅ K ) {A}_{M \times (M \cdot K \cdot K)} AM×(M⋅K⋅K) 的点乘。其中
W = [ w ( 1 ) w ( 2 ) ⋱ w ( M ) ] , \begin{equation*} {W}=\left[ \begin{array}{cccc} {w}^{(1)} & & & \\ & {w}^{(2)} & & \\ & & \ddots & \\ & & & {w}^{(M)} \\ \end{array}\right], \end{equation*} W= w(1)w(2)⋱w(M) ,
A = [ 1 1 × ( K ⋅ K ) 1 1 × ( K ⋅ K ) ⋱ 1 1 × ( K ⋅ K ) ] . \begin{equation*} {A}=\left[ \begin{array}{cccc} {1}_{1 \times (K \cdot K)} & & & \\ & {1}_{1 \times (K \cdot K)} & & \\ & & \ddots & \\ & & & {1}_{1 \times (K \cdot K)} \\ \end{array}\right]. \end{equation*} A= 11×(K⋅K)11×(K⋅K)⋱11×(K⋅K) .
深度卷积可以写成
W ^ = W ⊙ A Z = W ^ ⊗ X \begin{equation*} \begin{split} \hat{{W}} & = {W} \odot {A} \\ {Z} & = \hat{{W}} \otimes {X} \end{split} \end{equation*} W^Z=W⊙A=W^⊗X
其中 X {X} X 是输入特征图, Z {Z} Z 是输出特征图, ⊙ \odot ⊙ 表示元素乘法, ⊗ \otimes ⊗ 表示卷积。掩码矩阵 A {A} A 滤除冗余权重,只有深度权重参与卷积。在后向传播中,权重矩阵的梯度为
∂ Z ∂ W = ∂ Z ∂ W ^ ⋅ ∂ W ^ ∂ W = ∂ Z ∂ W ^ ⊙ A , \begin{equation*} \frac{\partial {Z}}{\partial {W}} = \frac{\partial {Z}}{\partial \hat{{W}}} \cdot \frac{\partial \hat{{W}}}{\partial {W}} = \frac{\partial {Z}}{\partial \hat{{W}}} \odot {A}, \end{equation*} ∂W∂Z=∂W^∂Z⋅∂W∂W^=∂W^∂Z⊙A,
其中也过滤掉多余的梯度,只激活深度权重。
###分组机制
与之前用于实现深度卷积的方法相比,由于权重向量的重构,我们的方法引入额外的计算成本,使得当输入通道的数量非常大时,我们的方法效率低下。我们提出了一个分组机制来解决这个问题,其中深度卷积被分成对角线组,并且对每个组执行对角线重构。
对于具有$ M $ 个输入通道的深度卷积,分组机制具有以下三个步骤:
- 首先,我们将输入通道分成 $ G $ 个组,每组包含 $ M / G $ 个通道。
- 其次,重构每组权重向量为该组的对角矩阵。
- 然后,每个组利用cuDNN库计算标准卷积。
通过这种方式,将 $ M $ 个通道的深度卷积转换成 $ G $ 个具有 $ M / G $ 输入通道的标准卷积,而不再是具有 $ M $ 输入通道的一个大标准卷积。
##实验
在本节中, 所有的实验都是在NVIDIA GTX 1080Ti GPU上进行的,每个结果取在训练过程中1000个批次的均值(批量大小为64)。
首先,专用内核方法提供比逐通道方法高得多的效率,但与标准卷积相比,具有稍差或相似的性能。我们的方法的Diagonalwise GEMM实现,在没有使用cuDNN或分组机制的情况下,比的所有逐通道方法都要好,但逊于专用内核方法。 当使用cuDNN(Diagonalwise cuDNN w/o grouping)时,除了TensorFlow之外,我们的方法提供比大多数专用内核方法更好的训练性能。最后,通过精心选择的分组策略(将在后面讨论),我们的方法(Diagonalwise cuDNN)超越了所有其他方法。
以Caffe为例,Diagonalwise GEMM比原来的C-by-C GEMM提供了$3.84 $ 倍的加速,而Diagonalwise cuDNN w/o grouping 和 Diagonalwise cuDNN提供了 1.72 × 1.72 \times 1.72× 和 1.27 × 1.27 \times 1.27× 的加速,从而使整体加速 8.4 8.4 8.4 ( ≈ 3.84 × 1.72 × 1.27 ) (\approx 3.84 \times 1.72 \times 1.27) (≈3.84×1.72×1.27) 倍。
###逐层实验
为了对以上方法进行详细比较,我们进一步逐层进行了实验来评估Caffe三种不同训练方法的时间。
从下表可以看出,逐通道方法(C-by-C GEMM)在最后几个层中的性能很差。这些层都具有宽且小的特征图,并且具有至少256个输入通道。他们都没有大于 28 × 28 28 \times 28 28×28 的特征图。对于C-by-C GEMM,小特征图仅会启动少量线程,并且GPU资源的利用率较低。例如,C-by-C GEMM的最后一个深度卷积层(第26层)与第一个(第2层)相比,只有 $ 1/8 $ 的线程。这放大了逐通道方法和其他方法之间的性能差距。

在前向传播期间,Diagonalwise cuDNN在整体训练时间上优于所有其他方法。Diagonalwise cuDNN比第一层中的Specialized Kernel更好,但是Specialized Kernel优于最后几层中的Diagonalwise cuDNN。这是因为小特征图通常会导致共享内存使用效率和缓存命中率更高,从而提高专用内核方法的性能。对于Diagonalwise cuDNN,与最后一层中的专用内核方法相比,当通道数很大时,在计算冗余和GPU利用率之间找到一个平衡是相对困难的,导致其性能略低。
在向后传播期间,Diagonalwise cuDNN明显优于其他方法。为了理解Specialized Kernel的糟糕表现,我们也评估了它在不计算权重梯度(Specialized Kernel ∗ ^* ∗)情况下的表现。 结果表明Specialized Kernel将大部分训练时间用于计算梯度。这是因为在计算梯度时有内存写入冲突,原子操作减慢了专用内核方法的整个训练过程。在前几个层中,这个问题更严重,特征图更大,存储器写冲突更频繁。cuDNN库中优化的内核和算法为我们的对角线重构方法提供了显着的加速。
下表使用三种方法来训练标准MobileNet,显示每种层类型的训练时间。与C-by-C GEMM和Specialized Kernel相比,使用对角重构方法(Diagonalwise cuDNN),用于训练深度卷积层的时间比率显着减少(至 45.41 % 45.41\% 45.41% )。
###分组策略
我们提出了两种分组策略并研究它们对训练表现的影响。
按数量分组
第一个策略是根据组的数量分组。假设组的数量是 $ G $ ,则每个深度卷积层被分成 $ G $ 个对角组,并且每个组包含 $ M / G $ 个通道。我们将 $ G $ 设置为从1到16,比较其效率,结果如图中所示。
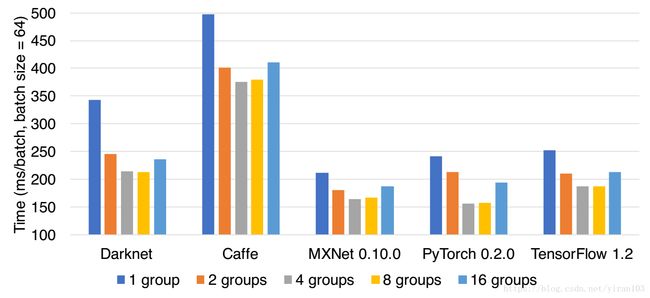
按大小分组
第二个策略是按组规模分组。假设组大小为 $ S $ 个通道,分组后每个深度卷积层将有 $ M / S $ 组。我们比较 $ S $ 从16到128的性能。下图显示不同配置下的结果。
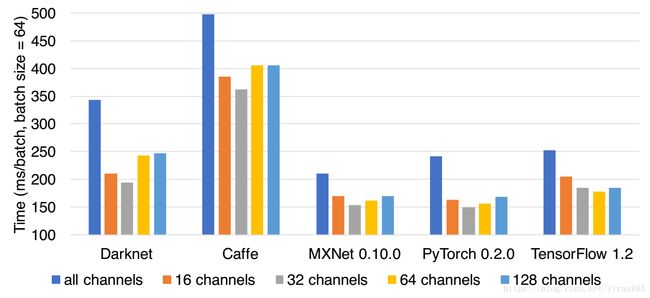
从两图可以看出,组策略的使用大大提高了我们方法的性能。与没有分组的方法相比,按数量分组提供 1.6 × 1.6 \times 1.6× 的加速,而按大小分组达到 1.76 × 1.76 \times 1.76× 加速。因为前几个薄层不会受到冗余计算的影响,所以按大小进行分组优于按数字分组。
##总结
MobileNets于2017年发表,其开创性设计使得模型计算量大幅减少。然而在很长一段时间里,MobileNets仅在TensorFlow下表现出速度优势,在其他框架下均水土不服。即使人工智能行业的一个主要推动者——NVIDIA在长达一年的时间内都没有跟进。仅有陈天奇的TVM可以优化深度卷积。考虑到谷歌还自研NPU,在此不得不佩服其在整个产业中的领导力。而从横向来看,作为第一代框架Caffe还是疲态尽显。知识以及研究具有时效性,arXiv.org的意义在于快速分享。就在4月份,NVIDIA发布的 cuDNN v7.0.4 优化了分组卷积的性能。已有大神在MXNet上测试cuDNN7.1比默认实现快数倍。然而这篇论文的贡献是不容抹杀的。因为cuDNN仅是一个闭源库,而这篇文章的思路和实践带我们一窥其中的原理。
只使用标准MobileNet的前11层。0.375表示宽度乘数,而416和128表示分辨率乘数。 ↩︎

