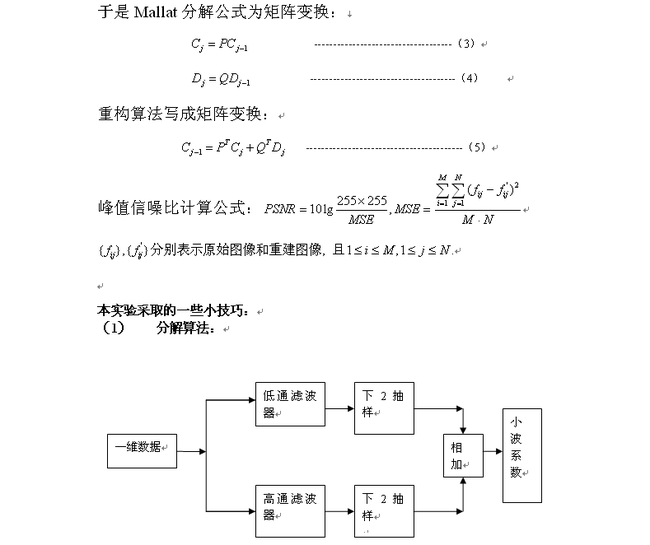
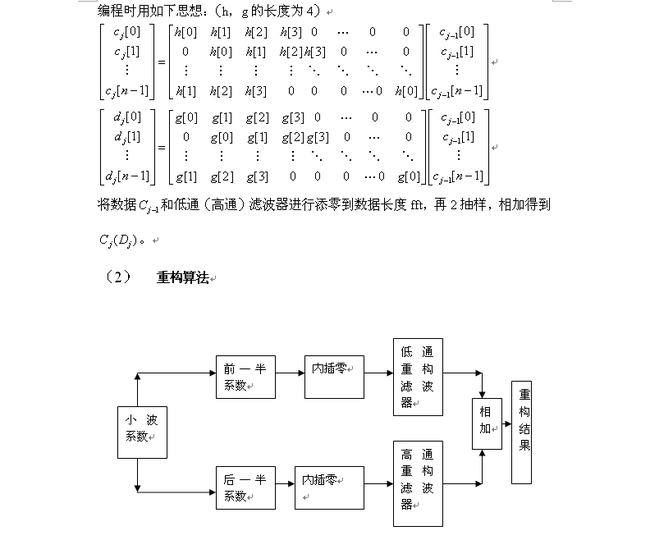
小波分析实验： 实验2 二维离散小波变换(Mallat快速算法)

实验目的：

在理解离散小波变换原理和Mallat快速算法的基础上，通过编程对图像进行二维离散小波变换，从而加深对二维小波分解和重构的理性和感性认识，并能提高编程能力，为今后的学习和工作奠定基础。

实验工具：

计算机，matlab6.5

附录：

（1）二维小波分解函数

%二维小波分解函数

 

function Y=mallatdec2(X,wname,level)

%输入:X      载入的二维图像像数值;

%     level  小波分解次(级)数设定值(如果设定值超过最高可分解次数,按最高分解次数分解)

%      wname  小波名字wavelet name

%输出：Y     多极小波分解后的小波系数矩阵

 

[h,g]=wfilters(wname,'d');  %h,g分别为低通和高通滤波器

X=double(X);

t=1;

hh=size(X,2);

 

while t<=level 

    %先进行行小波变换

    for  row=1:hh

        Y(row,1:hh)=mdec1(X(row,1:hh),h,g) ;

    end

    %再进行列小波变换

    for col=1:hh

        temp=mdec1( Y(1:hh,col)',h,g);

        Y(1:hh,col)=temp';

    end

t=t+1;

hh=hh/2;

X=Y;

end

 

%内部子函数，对一行(row)矢量进行一次小波变换，利用fft实现

function y=mdec1(x,h,g)

%输入：x 行数组

%     h为低通滤波器

%     g为高通滤波器

%输出： y 进行一级小波分解后的系数

lenx=size(x,2);

lenh=size(h,2);

 

rh=h(end:-1:1);

rrh=[zeros(1,(lenx-lenh)),rh];

rrh=circshift(rrh',1)';

 

rg=g(end:-1:1);

rrg=[zeros(1,(lenx-lenh)),rg];

rrg=circshift(rrg',1)';

r1=dyaddown(ifft(fft(x).*fft(rrh,lenx)),1);  %use para 1

r2=dyaddown(ifft(fft(x).*fft(rrg,lenx)),1);

y=[r1,r2];

 

（2）二维小波重构函数

%二维小波重构函数

function Y=mallatrec2(X,wname,level)

%输入:X      载入的小波系数矩阵;

%     level  小波分解次(级)数设定值(如果设定值超过最高可分解次数,按最高分解次数分解)

%      wname  小波名字wavelet name

%输出：Y     重构图像矩阵

 

[h,g]=wfilters(wname,'d');  %h,g分别为重构低通滤波器和重构高通滤波器

 

hz=size(X,2);

h1=hz/(2^(level-1));

while h1<=hz

    % 对列变换

    for col=1:h1

        temp=mrec1(X(1:h1,col)',h,g)';

        X(1:h1,col)=temp;

    end

    %再对行变换

    for row=1:h1

        temp=mrec1(X(row,1:h1),h,g);

         X(row,1:h1)=temp;

     end

     h1=h1*2;

    

end

Y=X;

 

 

 

%内部子函数，对一行小波系数进行重构

function y=mrec1(x,h,g)

%输入：x 行数组

%     h为低通滤波器

%     g为高通滤波器

%输出： y 进行一级小波重构后值

lenx=size(x,2);

 

 

r3=dyadup(x(1,1:lenx*0.5),0);   %内插零use para 0

r4=dyadup(x(1,(lenx*0.5+1):lenx),0);   %use para 0

y=ifft(fft(r3,lenx).*fft(h,lenx))+ ifft(fft(r4,lenx).*fft(g,lenx));  

 

（3）测试函数（主函数）

%测试函数（主函数）

clc;clear;

X=imread('E:\Libin的文档\Course\Course_wavelet\实验2要求\exp2\LENA.bmp');%路径

 X=double(X);

A = mallatdec2(X,'sym2',3);

 

image(abs(A));

colormap(gray(255));

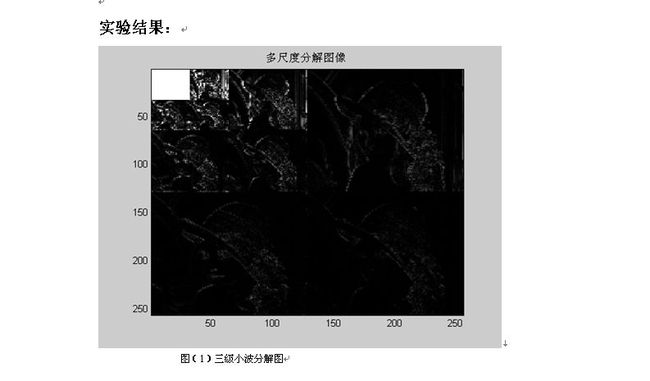
title('多尺度分解图像');

Y= mallatrec2(A,'sym2',3);

Y=real(Y);

figure(2);

subplot(1,2,1);

image(X);

colormap(gray(255));

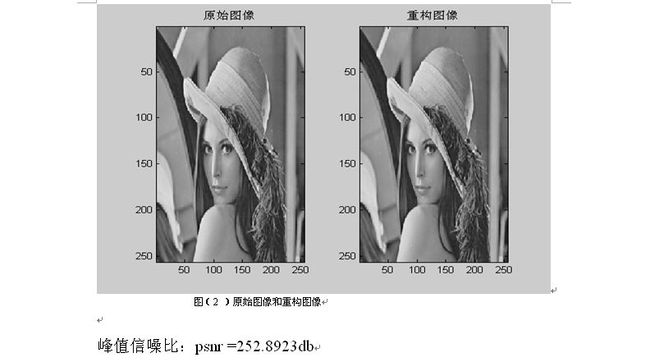
title('原始图像');

subplot(1,2,2);

image(Y);

colormap(gray(255));

title('重构图像');

csize=size(X);

sr=csize(1);

sc=csize(2);

mse=sum(sum( (Y-X).^2,1))/(sr*sc);

psnr=10*log(255*255/mse)/log(10)

Torstan

2005.09.22