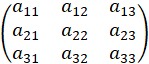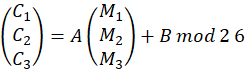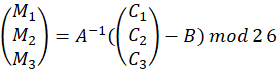多表代换加密解密(python实现)
多表代换加密解密(python实现):
多表代替密码:由多个简单的代替密码构成,例如,可能有5个被使用的不同的简单代替密码,单独的一个字符用来改变明文的每个字符的位置。其算法可简述为:设密钥为k,明文为m,加密为c,则有加密变换ek(m)=c1c2…cn,其中,ci=mi+ki mod q。其中Vigenere密码和Beaufort密码均是多表密码的实例。
1.密钥生成
(1)随机生成3ⅹ3可逆矩阵A,其中 :
计算其行列式并模去26,若其行列式等于零或与26不互素,则重新生成矩阵。
矩阵生成后,计算其在模26下的逆矩阵。
(2)生成3维向量 ,其中 。
(3)保存A,A-1,B作为秘密密钥。
2. 加密
- 输入一段英文,将其转变成0~25之间的整数,并将这些整数分为3个一组;
- 对于
 ,计算
,计算
- 循环加密直到所有的字母都加密完毕。
- 保存密文。
3. 解密
- 读入密文,将其转变成0~25之间的整数,并将这些整数分为3个一组;
- 对于
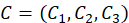 ,计算
,计算
- 循环解密直到所有的字母都解密完毕。
- 保存明文并将其与开始加密的明文进行比较,判断是否正确。
python实现源码:
# -*- coding: utf-8 -*-
"""
Created on Sat Nov 10 12:44:52 2018
@author: Baron
"""
import numpy as np
from numpy.linalg import *
def my_int_inv(mat, n=26):
x = np.zeros(mat.shape, dtype=np.int16)
for i in range(mat.shape[0]):
for j in range(mat.shape[1]):
x[i, j] = int(round(mat[i, j])) % n
return x
def gcd(a, b):
while a != 0:
a, b = b % a, a
return b
def exgcd(a, m):
if gcd(a, m) != 1:
return None
u1, u2, u3 = 1, 0, a
v1, v2, v3 = 0, 1, m
while v3 != 0:
q = u3 // v3
v1, v2, v3, u1, u2, u3 = (u1 - q * v1), (u2 - q * v2), (u3 - q * v3), v1, v2, v3
return u1 % m
a = np.mat([[11, 2, 19], [5, 23, 25], [20, 7, 17]])
b = np.mat([[3], [3], [2]])
m = np.mat([[24, 17, 13, 8, 14], [14, 15, 13, 18, 20], [20, 8, 14, 5, 17]])
c = a * m + b
c = my_int_inv(c)
a_inv = a.I
a_det = det(a)
a_adju = my_int_inv(a_det * a_inv)
a_det_inv = exgcd(int(round((det(a) % 26))), 26)
aa_inv = my_int_inv(a_det_inv * a_adju)
m = (aa_inv * (c - b)) % 26
print(m)