【Python机器学习】之 Linear 线性回归法

Linear 线性回归算法

  回归分析是一种预测性建模技术，主要用来研究因变量（$y_i$）和自变量（$x_i$）之间关系，通常被用于预测分析、时间序列等。

  线性回归（Linear Regression）是利用线性回归方程的最小二乘法对一个或多个自变量和因变量之间关系进行建模的方法。

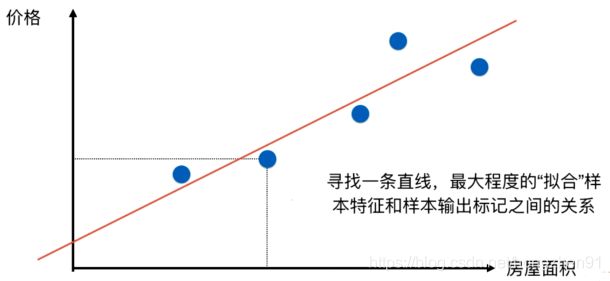
  假设一个房价-房屋面积数据信息情况如下图蓝点，通过线性回归方法拟合得到房价-房屋面积之间的线性关系，从而进行预测。

   线性回归与之前 kNN 算法区别，即分类问题和回归问题区别：

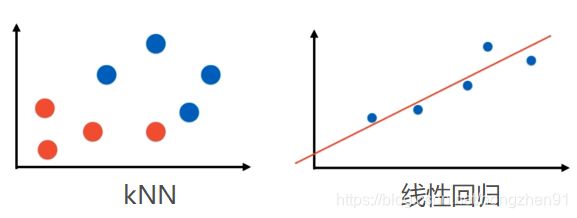
​ 在上图左边 kNN 算法，右边线性回归算法。两者在数据上有不同的特征：kNN算法中，横纵坐标均代表样本特征，样本点的颜色代表样本的分类；而线性回归中横坐标代表样本特征，纵坐标代表样本对应的标记值。

1、线性回归算法

1.1、特点：

• 解决回归问题
• 思想简单，容易实现
• 许多强大的非线性模型的基础
• 结果具有很好的可解释性
• 蕴含机器学习中的很多重要思想

1.2、线性回归应用

• 流行病学
  • 有关吸烟对死亡率和发病率影响的早期证据来自采用了回归算法
• 金融
  • 资本资产定价模型利用线性回归、分析和计算投资的系统风险
• 经济学
  • 线性回归是经济学的主要实证工具，例如用来预测消费支出

2、简单线性回归（一元）

2.1、线性回归（机器学习算法）基本思路

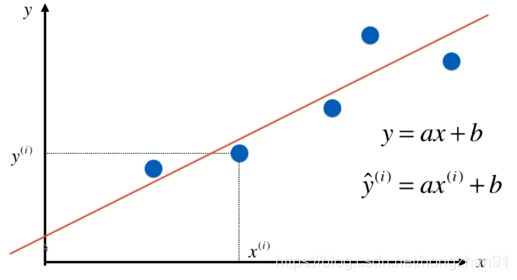
​ 假设可以找到最佳拟合的直线方程： $$y=ax+b$$

​ 则对于每个样本点$x^{(i)}$ ，根据得到的直线方程，可以得到预测值为：${\hat{y}}^{(i)}=ax+b$ ，真值为：$y^{(i)}$

​ 希望 $y^{(i)}$ 和 ${\hat{y}}^{(i)}$ 的差距尽可能的小，表达式 $$y^{(i)}$$ 和 $${\hat{y}}^{(i)}$$ 的差距为：$$y^{(i)}-{\hat{y}}^{(i)}$$

考虑到所有样本，即误差可能出现正负误差相抵的情况，所以采用误差平方和：

$$\sum _{i=1}^m(y^{(i)}-{\hat{y}}^{(i)}{)}^2$$

​ 目标：使上式尽可能的小，结合预测直线方程，可得：

即，使 $$\sum _{i=1}^m(y^{(i)}-a{x}^{(i)}+b{)}^2$$ 尽可能小，该式也叫损失函数（Loss Function）

求最大值的叫 效用函数（Utility Function）

• 通过分析问题，确定问题的损失函数或者效用函数；

• 通过优化损失函数或者效用函数，获得机器学习的模型。

近乎所有参数学习算法都是这样的思路：

1. 线性回归；
2. SVM ；
3. 多项式回归 ；
4. 神经网络 ；
5. 最优化原理 ；
6. 逻辑回归 ；
7. 凸优化 ； …

2.2、最小二乘法

目标： 使 $$\sum _{i=1}^m(y^{(i)}-a{x}^{(i)}+b{)}^2$$ 尽可能小

典型的最小二乘法问题：最小误差的平方

求$$J(a,b)=\sum _{i=1}^m(y^{(i)}-a{x}^{(i)}-b{)}^2$$最小值，采用链式求导法则
$$\{\begin{array}{l}\frac{\partial J(a,b)}{\partial a}=0\\ \frac{\partial J(a,b)}{\partial b}=0\end{array}$$
其中：
$$\frac{\partial J(a,b)}{\partial a}=2\sum _{i=1}^m(y^{(i)}-a{x}^{(i)}-b)(-x^{(i)})=0$$

$$\begin{gathered} \sum _{i=1}^m(y^{(i)}-a{x}^{(i)}-b)(-x^{(i)}) \\ =\sum _{i=1}^m(y^{(i)}-a(x^{(i)})-\hat{y}+a\overline{x})x^{(i)}=0 \end{gathered}$$

最终：
$$\begin{gathered} a=\frac{\sum _{i=1}^m(x^{(i)}-\overline{x})(y^{(i)}-\overline{y})}{\sum _{i=1}^m(x^{(i)}-\overline{x}{)}^2} \\ b=\overline{y}-a\overline{x} \end{gathered}$$

2.3、简单线性回归实现

（1）、自己编写实现：

import numpy as np
import matplotlib.pyplot as plt

x = np.array([1., 2., 3., 4., 5.])
y = np.array([1., 3., 2., 3., 5.])

x_mean = np.mean(x)
y_mean = np.mean(y)

num = 0.0  # 分子
d = 0.0   # 分母
for x_i, y_i in zip(x, y):
    num += (x_i  - x_mean) * (y_i - y_mean)
    d += (x_i - x_mean) ** 2
    
a = num/d
b = y_mean - a * x_mean

y_hat = a * x + b
plt.scatter(x, y)
plt.plot(x, y_hat, color='r')
plt.axis([0, 6, 0, 6])
plt.show()

运行结果：

进行预测：

x_predict = 6
y_predict = a * x_predict + b

# 输出：
# y_predict = 5.2

（2）、采用向量化方式实现：
$$\begin{gathered} a=\frac{{\sum }_{i=1}^m(x^{(i)}-\overline{x})(y^{(i)}-\overline{y})}{{\sum }_{i=1}^m(x^{(i)}-\overline{x}{)}^2} \\ b=\overline{y}-a\overline{x} \\ 由上观察：\sum _{i=1}^m{w}^{(i)}{v}^{(i)} \\ w=(w^{(1)},w^{(2)},...,w^{(i)}) \\ v=(v^{(1)},v^{(2)},...,v^{(i)}) \end{gathered}$$

import numpy as np


class SimpleLinearRegression1:

    def __init__(self):
        """初始化Simple Linear Regression 模型"""
        self.a_ = None
        self.b_ = None

    def fit(self, x_train, y_train):
        """根据训练数据集x_train,y_train训练Simple Linear Regression模型"""
        assert x_train.ndim == 1, \
            "Simple Linear Regressor can only solve single feature training data."
        assert len(x_train) == len(y_train), \
            "the size of x_train must be equal to the size of y_train"

        x_mean = np.mean(x_train)
        y_mean = np.mean(y_train)

        num = 0.0
        d = 0.0
        for x, y in zip(x_train, y_train):
            num += (x - x_mean) * (y - y_mean)
            d += (x - x_mean) ** 2

        self.a_ = num / d
        self.b_ = y_mean - self.a_ * x_mean

        return self

    def predict(self, x_predict):
        """给定待预测数据集x_predict，返回表示x_predict的结果向量"""
        assert x_predict.ndim == 1, \
            "Simple Linear Regressor can only solve single feature training data."
        assert self.a_ is not None and self.b_ is not None, \
            "must fit before predict!"

        return np.array([self._predict(x) for x in x_predict])

    def _predict(self, x_single):
        """给定单个待预测数据x，返回x的预测结果值"""
        return self.a_ * x_single + self.b_

    def __repr__(self):
        return "SimpleLinearRegression1()"

    
class SimpleLinearRegression2:
    """初始化Simple Linear Regression 模型"""
    def __init__(self):
        self.a_ = None
        self.b_ = None


    """根据训练数据集x_train,y_train训练Simple Linear Regression模型"""
    def fit(self, x_train, y_train):
        assert x_train.ndim == 1, \
            "Simple Linear Regressor can only solve single feature training data."
        assert len(x_train) == len(y_train), \
            "the size of x_train must be equal to the size of y_train"

        x_mean = np.mean(x_train)
        y_mean = np.mean(y_train)

        num = (x_train - x_mean).dot(y_train - y_mean)
        d = (x_train - x_mean).dot(x_train - x_mean)


        self.a_ = num / d
        self.b_ = y_mean - self.a_ * x_mean

        return self

    """给定待预测数据集x_predict，返回表示x_predict的结果向量"""
    def predict(self, x_predict):
        assert x_predict.ndim == 1, \
            "Simple Linear Regressor can only solve single feature training data."
        assert self.a_ is not None and self.b_ is not None, \
            "must fit before predict!"

        # 返回的数据类型是np对应的数组
        return np.array([self._predict(x)for x in x_predict])


    """给定单个待预测数据x，返回x的预测结果值"""
    def _predict(self, x_single):
        return self.a_ * x_single + self.b_

    def __repr__(self):
        return "SimpleLinearRegression2()" 

调用实现：

from playML.SimpleLinearRegression import SimpleLinearRegression2

reg2 = SimpleLinearRegression2()
reg2.fit(x, y)
reg2.predict(np.array([x_predict]))

# 输出：
# reg2.a_ = 0.8
# reg2.b_ = 0.39999999999999947

性能对比：

m = 1000000
big_x = np.random.random(size=m)
big_y = big_x * 2 + 3 + np.random.normal(size=m)
%timeit reg1.fit(big_x, big_y)
%timeit reg2.fit(big_x, big_y)

# 870 ms ± 14 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
# 14.5 ms ± 361 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)

# 输出：
# reg1.a_ = 2.003362104755884
# reg1.b_ = 2.9973974057901596
# reg2.a_ = 2.0033621047558086
# reg2.b_ = 2.9973974057901973

2.3、线性回归测评

由于上式中衡量标准公式是误差累加求和，这会引入测试数据集数量大小的影响，比如10个测试数据的累积误差是100，另一份测试数据集一共1000个数据，累积误差是120，明显不能够说第一份测试数据集得到的模型比第二份数据集得到的模型更好。所以，为了统一化，对上式除以 m ，使衡量标准与测试集数量 m 无关。

2.3.1、MSE(Mean Squared Error)

均方误差MSE:
$$MSE=\frac{1}{m}\sum _{i=1}^m(y_{test}^{(i)}-{\hat{y}}_{test}^{(i)}{)}^2$$

2.3.2、RRMSE(Root Mean Squared Error)

均方根误差RMSE:
$$\sqrt{\frac{1}{m}\sum _{i=1}^m(y_{test}^{(i)}-{\hat{y}}_{test}^{(i)}{)}^2}=\sqrt{MSE}$$
此时，仍然存在一个问题，即量纲。比如 y 代表房价（万元），均方误差的结果是，$y^2$，代表万元的平方，所以对均方误差进行开根号，和 y 统一量纲。

2.3.3、MAE(Mean Absolute Error)

对于线性回归算法，还有另外一个评判方法，即平均绝对误差 MAE。

平均绝对误差MAE：
$$MAE=\frac{1}{m}\sum _{i=1}^m|y_{test}^{(i)}-{\hat{y}}_{test}^{(i)}{|}^2$$

2.3.4 MSE vs MAE

RMSE 略大于 MAE，原因在于 RMSE 相当于对错误值平方求和之后再开方，如果错误值非常大，所以 RMSE 有放大错误偏差的作用。所以，尽量让 RMSE 的值尽可能小，实际更准确，意义更大一些。

RMSE 和 MAE 在量纲上是一样的，但是通过实际结果可以发现，但是 RMSE 比 MAE 稍微偏大。这是因为 RMSE 是把误差平方求和之后再开方，而 MAE 是直接对误差进行计算。所以 RMSE 有放大误差的作用，所以从某种程度上，让 RMSE 尽量小，则目标函数模型效果更好。

2.4.5 实现

波士顿房产数据

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

boston = datasets.load_boston()
x = boston.data[:,5] # 只使用房间数量这个特征
y = boston.target

np.max(y)  #  50.0
# 因为实际场景中，采集数据点时，有可能大于50的数据全都归为50一类，所以和
# 真实值可能存在偏差，所以去掉这些数据点
x = x[y < 50.0]  # 获取 y < 50 对应的 x 的数据集
y = y[y < 50.0]

from playML.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(x, y, seed=666)

from playML.SimpleLinearRegression import SimpleLinearRegression
reg = SimpleLinearRegression()
reg.fit(x_train, y_train)

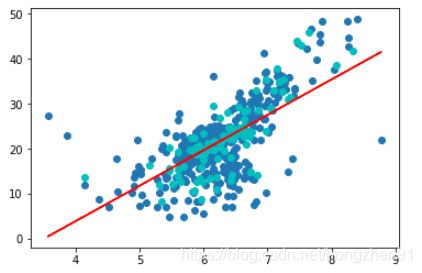
plt.scatter(x_train, y_train)
plt.scatter(x_test, y_test, color="c")
plt.plot(x_train, reg.predict(x_train), color='r')
plt.show()

（1）、MSE:

mse_test = np.sum((y_predict - y_test)**2) / len(y_test)
# 输出：24.156602134387438

（2）、RMSE:

from math import sqrt
rmse_test = sqrt(mse_test)

# 输出：4.914936635846635

（3）、MAE:

mae_test = np.sum(np.absolute(y_predict - y_test))/len(y_test)
# 输出：3.5430974409463873

3、多元线性回归

3.1、误差分析

对于分类而言，分类的准确度是在 0 和 1 之间判断，是 1 说明预测对了，是 0 反之。然后再预测问题中，不能同分类一样这么进行判断。所以引入了 $R^2$，计算方式如下：
$$R^2=1-\frac{S{S}_{residual}}{S{S}_{total}}=1-\frac{\sum _i({\hat{y}}^{(i)}-y^{(i)}{)}^2}{\sum _i(\overline{y}-y^{(i)}{)}^2}$$

分子：残差平方和

分母：总离差平方和

对公式进行详细分析：
分子描述：使用我们的模型预测产生的误差
分母描述：使用 $$y=\overline{y}$$ 预测产生的误差
其中，分母也叫 Baseline Model，因为这里不考虑 x ，直接预测 $\overline{y}$和样本数据$y^i$之间的误差，这样会产生很多的误差错误，而分子考虑了 x 对模型预测结果的作用，所以误差应该是会偏小的，会减少一些只考虑 y 产生的误差，同时也会产生一些由 x 引入的错误。所以通过，所以通过公式计算可以得到模型拟合住的那些数据，所以公式最终求解得到的是模型没有产生错误的指标。

所以由上式可以得到以下结论：

• $R^2<=1$
• $R^2$越大越好，当预测的模型没有产生任务错误时，得到的最大值是 1
• 当模型等于基准模型（Baseline Module）的时候，$R^2=0$
• $R^2<0$，说明模型还不如基准模型（即训练的模型还不如不训练）。此时，很可能数据不存在任何线性关系

3.2、多元回归推导：

求解多元线性回归
$$目标：使\sum _{i=1}^m(y^{(i)}-{\hat{y}}^{(i)}{)}^2尽可能小$$
$${\hat{y}}^{(i)}={\theta }_0+{\theta }_1{X}_1^{(1)}+{\theta }_2{X}_2^{(2)}+...+{\theta }_n{X}_n^{(i)}$$
$$\theta =({\theta }_0,{\theta }_1,...,{\theta }_n{)}^T$$

$$其中，{\theta }_0为截距，{\theta }_1,...,{\theta }_n为系数$$
所以，目标：$$找到{\theta }_0,{\theta }_1,...,{\theta }_n，使得\sum _{i=1}^m(y^{(i)}-{\hat{y}}^{(i)}{)}^2尽可能小$$
$$X=(X_0,X_1,...,X_n),X_0\equiv 1$$
所以，最终可得：

$$\left(\begin{array}{ccccc}1& X_1^{(1)}& X_1^{(1)}& \cdots & X_1^{(1)}\\ 1& X_1^{(2)}& X_2^{(2)}& \cdots & X_2^{(2)}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 1& X_1^{(m)}& X_2^{(m)}& \cdots & X_n^{(m)}\end{array}\right)$$
$$\hat{y}=X^{(i)}\cdot \theta$$

$$目标：使\sum _{i=1}^m(y^{(i)}-{\hat{y}}^{(i)}{)}^2尽可能小$$
$$目标：使(y-X_b\cdot \theta {)}^T\cdot (y-X_b\cdot \theta )尽可能小$$
应用最小二乘法，最终得：

$$\theta =(X_b^T{X}_b{)}^{-1}{X}_b^{T}y$$

3.4、多元线性回归实现

预测平安银行股票：

import numpy as np # 数学计算
import pandas as pd # 数据处理, 读取 CSV 文件 (e.g. pd.read_csv)
import matplotlib.pyplot as plt
from datetime import datetime as dt

df = pd.read_csv('./000001.csv') 

# 将每一个数据的键值的类型从字符串转为日期

df['date'] = pd.to_datetime(df['date'])
df = df.set_index('date')
# 按照时间升序排列
df.sort_values(by=['date'], inplace=True, ascending=True)
df.tail()

# 检测是否有缺失数据 NaNs

df.dropna(axis=0 , inplace=True)   # 0='index'
df.isna().sum()  # 统计缺失值个数

Min_date = df.index.min()
Max_date = df.index.max()
print ("First date is",Min_date)
print ("Last date is",Max_date)
print (Max_date - Min_date)

from plotly import tools
from plotly.graph_objs import *
from plotly.offline import init_notebook_mode, iplot, iplot_mpl
init_notebook_mode()
import plotly.plotly as py
import plotly.graph_objs as go

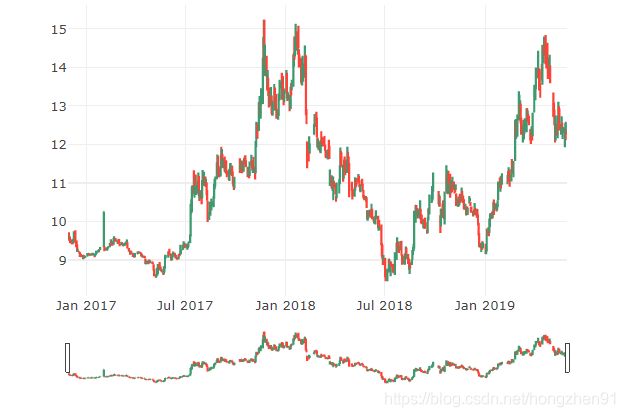
trace = go.Ohlc(x=df.index, open=df['open'], high=df['high'], low=df['low'], close=df['close'])
data = [trace]
iplot(data, filename='simple_ohlc')

from sklearn.linear_model import LinearRegression
from sklearn import preprocessing

# 创建新的列, 包含预测值, 根据当前的数据预测5天以后的收盘价
num = 5 # 预测5天后的情况
df['label'] = df['close'].shift(-num) # 预测值
                                     
# 丢弃 'label', 'price_change', 'p_change', 不需要它们做预测
Data = df.drop(['label', 'price_change', 'p_change'],axis=1)

X = Data.values
X = preprocessing.scale(X)
X = X[:-num]

df.dropna(inplace=True)
Target = df.label
y = Target.values

# 将数据分为训练数据和测试数据
X_train, y_train = X[0:550, :], y[0:550]
X_test, y_test = X[550:, -51:], y[550:606]

lr = LinearRegression()
lr.fit(X_train, y_train)
lr.score(X_test, y_test) # 使用绝对系数 R^2 评估模型

# 做预测 

X_Predict = X[-num:]
Forecast = lr.predict(X_Predict)

画出预测结果图：

# 预测 2019-05-13 到 2019-05-17 , 一共 5 天的收盘价 
trange = pd.date_range('2019-05-13', periods=num, freq='d')

# 产生预测值dataframe
Predict_df = pd.DataFrame(Forecast, index=trange)
Predict_df.columns = ['forecast']

# 将预测值添加到原始dataframe
df = pd.read_csv('./000001.csv') 
df['date'] = pd.to_datetime(df['date'])
df = df.set_index('date')
# 按照时间升序排列
df.sort_values(by=['date'], inplace=True, ascending=True)
df_concat = pd.concat([df, Predict_df], axis=1)

df_concat = df_concat[df_concat.index.isin(Predict_df.index)]

# 画预测值和实际值
df_concat['close'].plot(color='green', linewidth=1)
df_concat['forecast'].plot(color='orange', linewidth=3)
plt.xlabel('Time')
plt.ylabel('Price')
plt.show()

3.3、更多关于线性回归

多元线性回归的正规方程解（Normal Equation）
$$\theta =(X_b^T{X}_b{)}^{-1}{X}_b^{T}y$$

• 问题：时间复杂度高：$$O(n^3)，优化后仍高达O(n^2.4)$$
• 优点：不需要对数据做归一化处理
• 解决方法：采用梯度下降法求解

---

文中实例参考：

• 贪心学院，https://www.greedyai.com
• 刘宇波老师《Python入门机器学习》