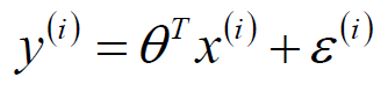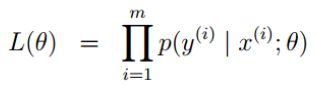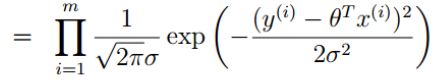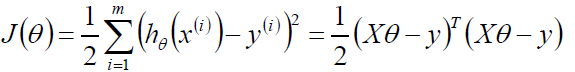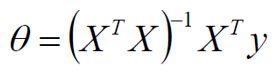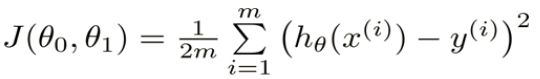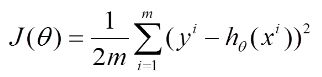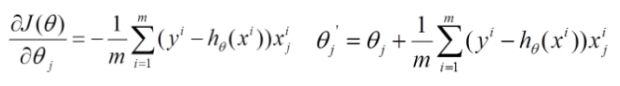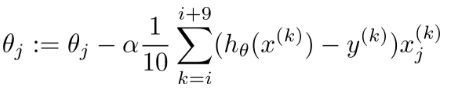线性回归原理推导及代码实现

1.线性回归概述

实例：

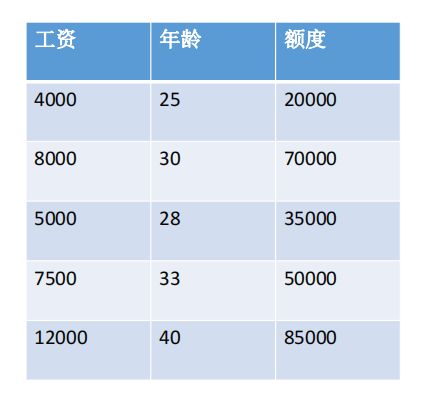
数据：工资和年龄（2个特征）

目标：预测银行会贷款给我多少钱（标签）

考虑：工资和年龄都会影响最终银行贷款的结果那么它们各自有多大的影响呢？（参数）

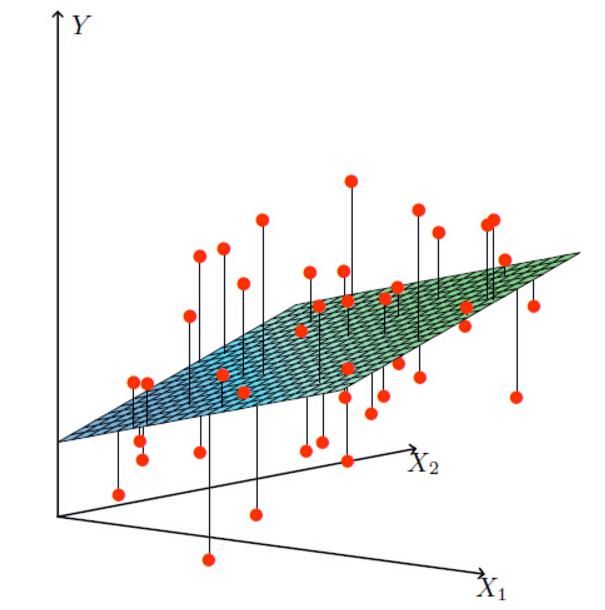
X1,X2就是我们的两个特征（年龄，工资）Y是银行最终会借给我们多少钱

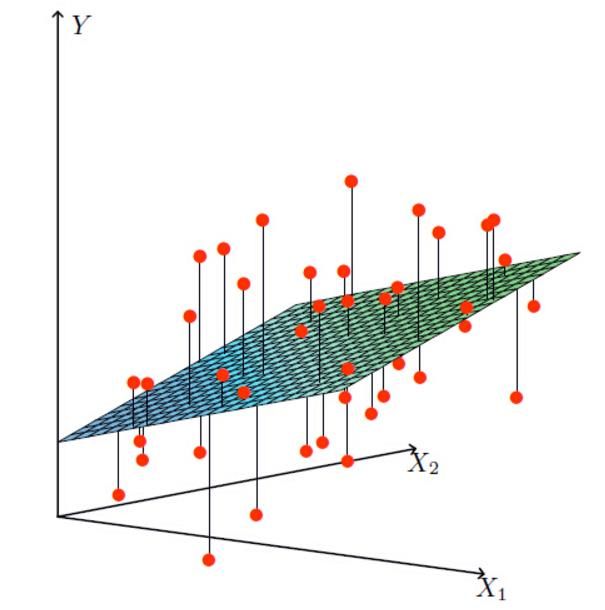
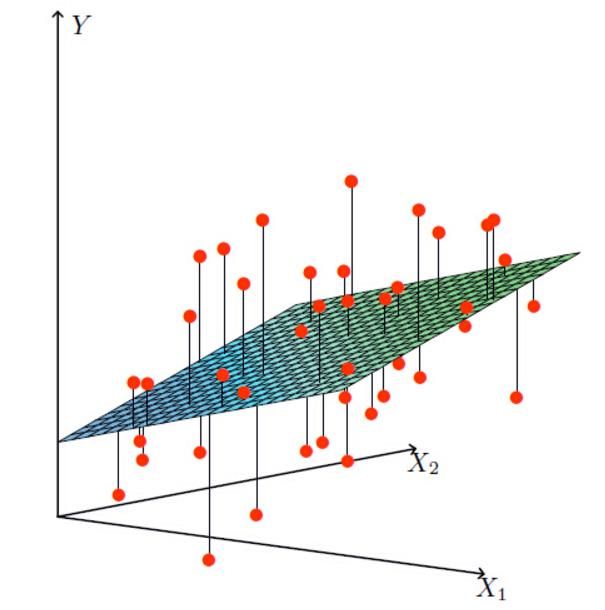
找到最合适的一条线（想象一个高维）来最好的拟合我们的数据点

 

 

 误差：

真实值和预测值之间肯定是要存在差异的（用 来表示该误差）

对于每个样本： 

 独立同分布：

独立：数据之间没有任何影响

同分布：所有数据均来自于同一分布

在实际应用中，数据尽可能满足上诉条件既可以使用

2.极大似然估计 

似然函数： 

 解释：什么样的参数跟我们的数据组合后恰好是真实值

对数似然：

 解释：乘法难解，加法就容易了，对数里面乘法可以转换成加法

展开化简：

 目标：让似然函数（对数变换后也一样）越大越好

 

 目标函数：

 求偏导：

 偏导等于0：

 3.梯度下降

目标函数：  

寻找山谷的最低点，也就是我们的目标函数终点（什么样的参数能使得目标函数达到极值点）

梯度下降，目标函数：

 批量梯度下降：

 （容易得到最优解，但是由于每次考虑所有样本，速度很慢）

随机梯度下降：

 （每次找一个样本，迭代速度快，但不一定每次都朝着收敛的方向）

 小批量梯度下降法：

 （每次更新选择一小部分数据来算，实用！）

学习率（步长）：对结果会产生巨大的影响，一般小一些

如何选择：从小的时候，不行再小

批处理数量：32，64，128都可以，很多时候还得考虑内存和效率

4.代码实现 

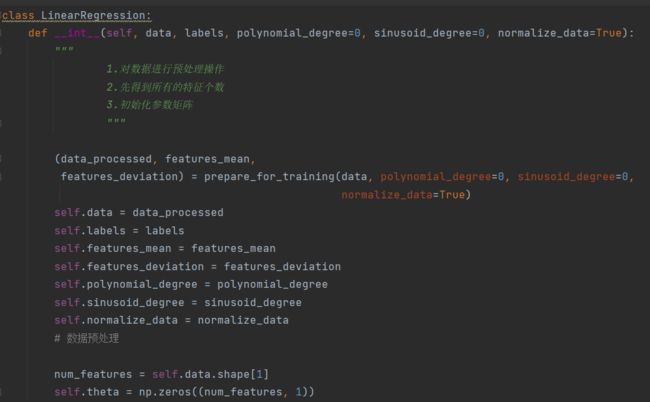
        线性回归代码实现 

 实验分析：

单变量

import sys
sys.path.append('E:/PycharmProjects/machine learning/code refactoring/线性回归-代码实现/')
sys.path.append('E:/PycharmProjects/machine learning/code refactoring/线性回归-代码实现/LinearRegression')
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

from linear_regression1 import LinearRegression

data = pd.read_csv('E:/PycharmProjects/machine learning/code refactoring/线性回归-代码实现/data/world-happiness-report-2017.csv')

# 得到训练和测试数据
train_data = data.sample(frac = 0.8)
test_data = data.drop(train_data.index)

input_param_name = 'Economy..GDP.per.Capita.'
output_param_name = 'Happiness.Score'

x_train = train_data[[input_param_name]].values
y_train = train_data[[output_param_name]].values

x_test = test_data[input_param_name].values
y_test = test_data[output_param_name].values

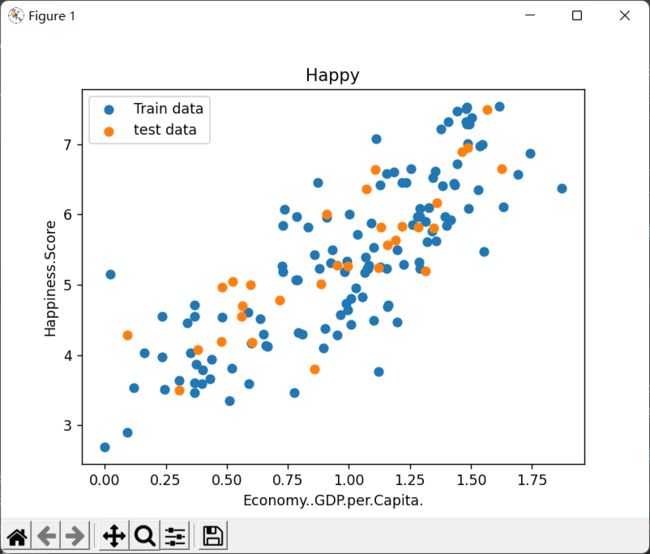
plt.scatter(x_train,y_train,label='Train data')
plt.scatter(x_test,y_test,label='test data')
plt.xlabel(input_param_name)
plt.ylabel(output_param_name)
plt.title('Happy')
plt.legend()
plt.show()

num_iterations = 500
learning_rate = 0.01

linear_regression = LinearRegression(x_train,y_train)
(theta,cost_history) = linear_regression.train(learning_rate,num_iterations)

print ('开始时的损失：',cost_history[0])
print ('训练后的损失：',cost_history[-1])

plt.plot(range(num_iterations),cost_history)
plt.xlabel('Iter')
plt.ylabel('cost')
plt.title('GD')
plt.show()

predictions_num = 100
x_predictions = np.linspace(x_train.min(),x_train.max(),predictions_num).reshape(predictions_num,1)
y_predictions = linear_regression.predict(x_predictions)

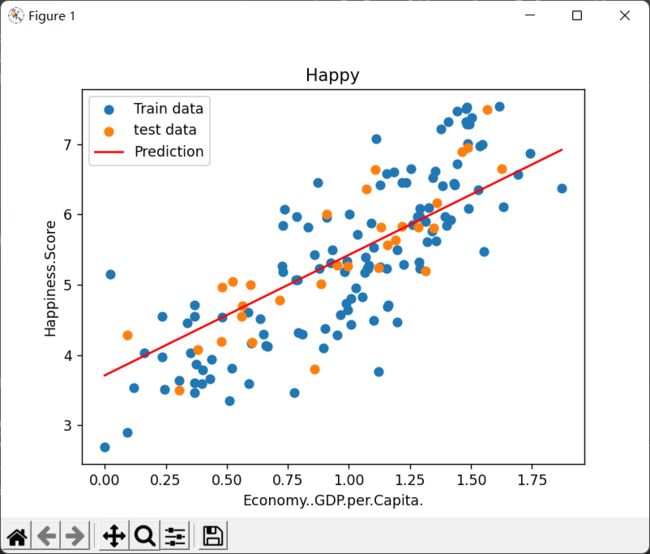
plt.scatter(x_train,y_train,label='Train data')
plt.scatter(x_test,y_test,label='test data')
plt.plot(x_predictions,y_predictions,'r',label = 'Prediction')
plt.xlabel(input_param_name)
plt.ylabel(output_param_name)
plt.title('Happy')
plt.legend()
plt.show()

数据情况： 

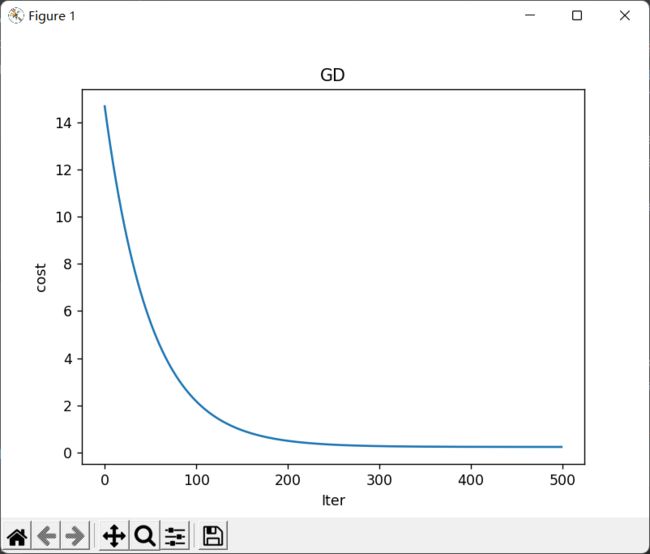
损失情况： 

 决策边界：

 开始时的损失： 14.686657434569007
训练后的损失： 0.23474965096256492

多变量实验分析

数据情况：

import sys
sys.path.append('E:/PycharmProjects/machine learning/code refactoring/线性回归-代码实现/')

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import plotly
import plotly.graph_objs as go

# plotly.offline.init_notebook_mode()
from linear_regression1 import LinearRegression

data = pd.read_csv('E:/PycharmProjects/machine learning/code refactoring/线性回归-代码实现/data/world-happiness-report-2017.csv')

train_data = data.sample(frac=0.8)
test_data = data.drop(train_data.index)

input_param_name_1 = 'Economy..GDP.per.Capita.'
input_param_name_2 = 'Freedom'
output_param_name = 'Happiness.Score'


x_train = train_data[[input_param_name_1, input_param_name_2]].values
y_train = train_data[[output_param_name]].values

x_test = test_data[[input_param_name_1, input_param_name_2]].values
y_test = test_data[[output_param_name]].values

# Configure the plot with training dataset.
plot_training_trace = go.Scatter3d(
    x=x_train[:, 0].flatten(),
    y=x_train[:, 1].flatten(),
    z=y_train.flatten(),
    name='Training Set',
    mode='markers',
    marker={
        'size': 10,
        'opacity': 1,
        'line': {
            'color': 'rgb(255, 255, 255)',
            'width': 1
        },
    }
)


plot_test_trace = go.Scatter3d(
    x=x_test[:, 0].flatten(),
    y=x_test[:, 1].flatten(),
    z=y_test.flatten(),
    name='Test Set',
    mode='markers',
    marker={
        'size': 10,
        'opacity': 1,
        'line': {
            'color': 'rgb(255, 255, 255)',
            'width': 1
        },
    }
)


plot_layout = go.Layout(
    title='Date Sets',
    scene={
        'xaxis': {'title': input_param_name_1},
        'yaxis': {'title': input_param_name_2},
        'zaxis': {'title': output_param_name} 
    },
    margin={'l': 0, 'r': 0, 'b': 0, 't': 0}
)

plot_data = [plot_training_trace, plot_test_trace]

plot_figure = go.Figure(data=plot_data, layout=plot_layout)

plotly.offline.plot(plot_figure)

num_iterations = 500  
learning_rate = 0.01  
polynomial_degree = 0  
sinusoid_degree = 0  

linear_regression = LinearRegression(x_train, y_train, polynomial_degree, sinusoid_degree)

(theta, cost_history) = linear_regression.train(
    learning_rate,
    num_iterations
)

print('开始损失',cost_history[0])
print('结束损失',cost_history[-1])

plt.plot(range(num_iterations), cost_history)
plt.xlabel('Iterations')
plt.ylabel('Cost')
plt.title('Gradient Descent Progress')
plt.show()

predictions_num = 10

x_min = x_train[:, 0].min();
x_max = x_train[:, 0].max();

y_min = x_train[:, 1].min();
y_max = x_train[:, 1].max();


x_axis = np.linspace(x_min, x_max, predictions_num)
y_axis = np.linspace(y_min, y_max, predictions_num)


x_predictions = np.zeros((predictions_num * predictions_num, 1))
y_predictions = np.zeros((predictions_num * predictions_num, 1))

x_y_index = 0
for x_index, x_value in enumerate(x_axis):
    for y_index, y_value in enumerate(y_axis):
        x_predictions[x_y_index] = x_value
        y_predictions[x_y_index] = y_value
        x_y_index += 1

z_predictions = linear_regression.predict(np.hstack((x_predictions, y_predictions)))

plot_predictions_trace = go.Scatter3d(
    x=x_predictions.flatten(),
    y=y_predictions.flatten(),
    z=z_predictions.flatten(),
    name='Prediction Plane',
    mode='markers',
    marker={
        'size': 1,
    },
    opacity=0.8,
    surfaceaxis=2, 
)

plot_data = [plot_training_trace, plot_test_trace, plot_predictions_trace]
plot_figure = go.Figure(data=plot_data, layout=plot_layout)
plotly.offline.plot(plot_figure)