C++ BinarySercahTree for version
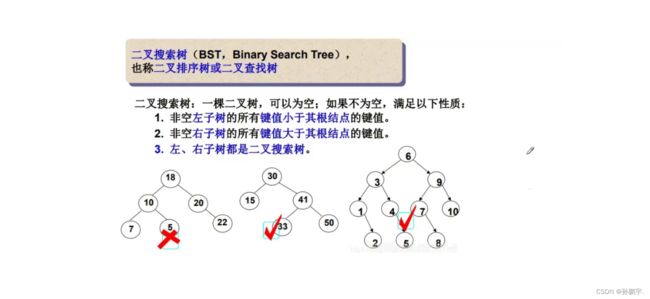
搜索二叉树定义
搜索二叉树模拟实现
首先写一个模版，然后写一个搜索二叉树的类 BSTree，类里面给 BSTe进行重命名为：Node。
template
class BSTree
{
tyepdef BSTree Node;
private:
Node* root = nullptr;
};
再写一个搜二叉的结构体
template
struct BSTreeNode
{
BSTreeNode< K>* _left;
BSTreeNode< K>* _right;
K _key;
}; 初始化列表：
struct BSTreeNode
{
BSTreeNode< K>* _left;
BSTreeNode< K>* _right;
K _key;
BSTree
:_left(nullptr)
,_right(nullptr)
,_key(key)
{
}
};插入
如果根节点为空，就开辟一个节点，然后把要插入的值给这个节点：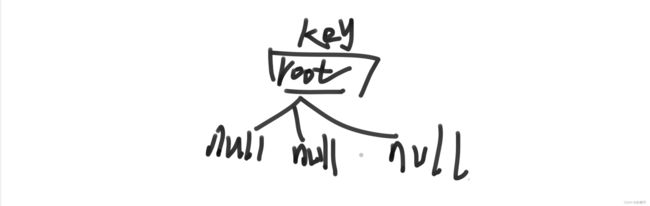
bool Insert(const k& key)
{
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
}如果跟节点不为空，就按搜索二叉树的性质来插入
即：如果key值比root值大，就把key值插在root节点右边，否则就插在root节点左边。
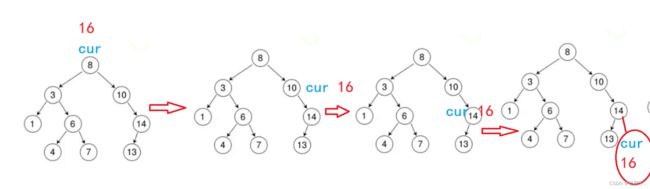
假如下图这个搜二叉，我们要插入个key=16，该怎么插：
插入的历程如下：
code
else{
Node* cur = _root;
if (cur->_key < key)//如果key大
{
cur = cur->_right; //往右走
}
else if (cur->_key > key) //如果key小
{
cur = cur->_left; //往左走
}
}还有一种情况，那就是如果插入值和cur相等呢？
搜二叉不允许节点值相等，所以这就是为什么Insert函数给bool类型的原因。
如果相等就return false;
else
{
Node* cur = _root;
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return false;
}上面的只是走一次，走到哪里结束呢？还需要再加个限制条件，我们让cur走到空的时候就不走了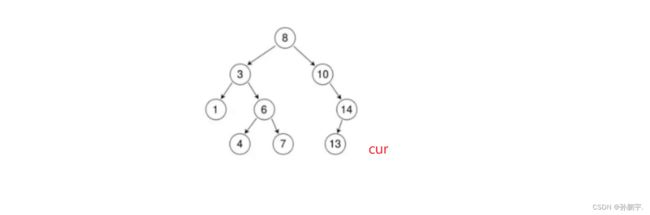
当while（cur为空就不走了）：
else{
while (cur)
{
Node* cur = _root;
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return false;
}
}
}开始插入
在为空的地方开辟一个新节点，把要插入的值push进这个新节点
else
{
while (cur)
{
Node* cur = _root;
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(key);
return true;
}ps:
虽然把值push进新节点了，但是此时新节点与搜二叉是一个断层状态，我们还需要把它们链起来。
可以弄一个快慢指针，cur先走，parent再走，当cur走完了，parent正好是cur的父亲节点，再把他俩链起来。
Node* cur = _root;
Node* parent = nullptr;
else
{
while (cur)
{
parent = cur;
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(key);
if (cur->key < parent->_key)cur = parent->left;
else if (cur->key > parent->_key)cur = parent->_right;
return true;
}遍历
写一个中序来遍历
void Inorder(Node * root)
{
if (root == nullptr)return;
Inorder(root->_left);
cout << root->_key << " ";
Inorder(root->_right);
}cout << endl;写完了我们现在要调用Inorder
main
BSTree bt;
bt.Inorder(); 递归调用需要传参，我们应该传个root给inorder（）。但是我们在main函数里拿不到root,列如：
方法一，写一个getroot函数，返回root，我们调用getroot就行了：
Node* getroot()
{
return root;
}main
bt.Inorder(bt.getroot());方法2：我们外层写一个递归INORDER（）,里面嵌套我们的_INORDER（），以此实现递归：
void _Inorder(Node * root)
{
if (root == nullptr)return;
_Inorder(root->_left);
cout << root->_key << " ";
_Inorder(root->_right);
}cout << endl;
void Inorder()
{
_Inoreder(_root);
}main
bt.Inorder( );
查找
查找key值，如果key比cur大就往右找，否则往左找，如果找到节点为空都找不到，返回false。如果找到了，返回true
bool Find(const K& key)
{
Node* cur = _root;
if (_root == nullptr)return;
if (cur->_key < key)
{
cur = cur->right;
}
else if (cur->_key > key)
{
cur = cur->left;
}
else
{
//找遍了就是没找到，return false;
return false;
}
return true;//否则找到节点为空就是找到了，return true；
}
删除
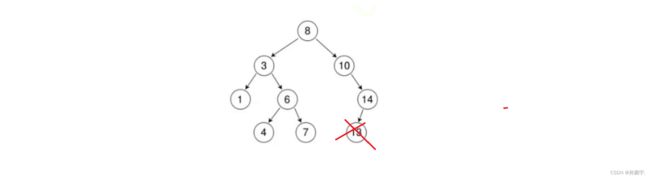
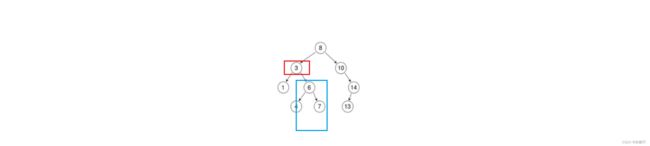
我们都知道叶子节点最好删除，只要置空，然后free掉就可以了，如下图:
假设我们要删除根节点呢？
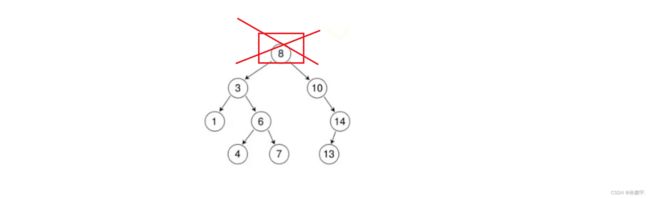
根据之前写二叉树的经验，根节点不能直接删除，再把其他节点挪上来，否则会改变树的结构。
而根节点处理好了，删除其他节点都可以按一样的方法进行处理。
我们可以用替换法，就是找一个节点与要交换的节点进行交换，但是交换之后仍然要保证搜二叉地的特性。
比如我可以把值为8节点和值为7节点进行交换：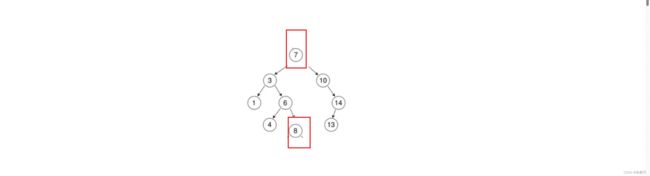
也可以把值为8节点与值为10节点交换：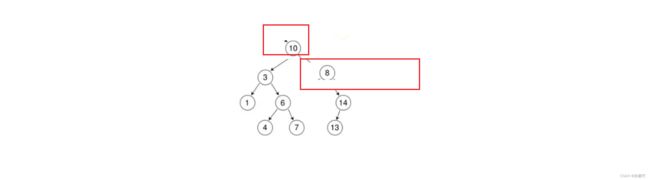
我们发现规律：与左子树最大的值的节点交换/与右子树最小的值的节点交换。
然后再置空，free：
注意点:
先写出框架：
bool Erase(const K& key )
{
Node* parent = nullptr; //初始化
Node* cur = root;
//要删除数如果大于root就往右走
if (cur->_key < key)
{
cur = cur->right;
}
//要删除数如果大于root就往左走
else if (cur->_key > key)
{
cur = cur->left;
}
else
{
//走到空，相等了，相等就是找到了
//找到了就准备删除
}
}
然后来写删除的具体步骤：
我们把8删掉了，就断层了：
我们需要重新链起来，可以这样写：
key->right=root->right
但是这样不完善，因为万一被删除的节点左边还有节点呢？
所以还要写一个
key->left=root->right
code
Node* parent = nullptr; //初始化
Node* cur = root;
if (cur->left == nullptr)
{
if (cur = parent->left)
{
parent->left = cur->right;
}
else if(cur = parent->right)
{
parent->right = cur->right;
}
}
else if (cur->right == nullptr)
{
if (cur = parent->left)
{
parent->left = cur->left;
}
else if (cur = parent->right)
{
parent->right = cur->left;
}
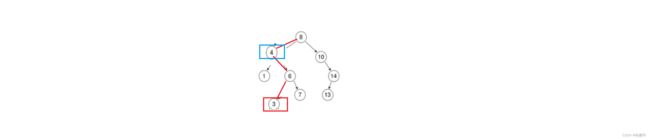
}诈一看，好像没什么大问题，但实际上有纰漏。代码漏了一种情况，那就是下图这种情况：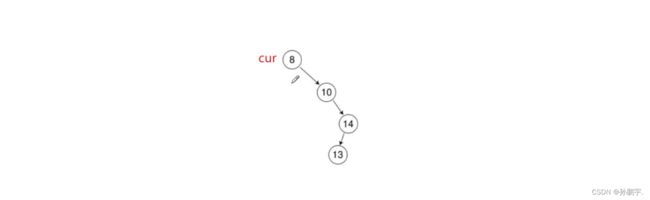
cur=8=root=key，8就是我们要删除的节点，8没有parent。
所以还需要加个条件：
if (cur == parent->left)
{
cur = cur->right;
} 
if (cur = parent->left)
{
parent->left = cur->left;
}
还有一种情况，就是左右子树都不为空，例如3节点：
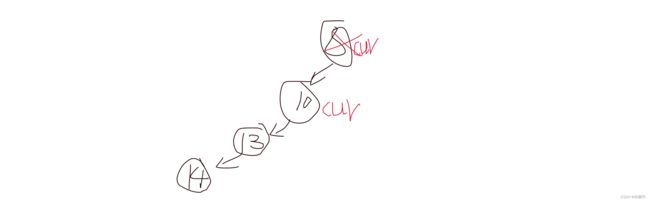
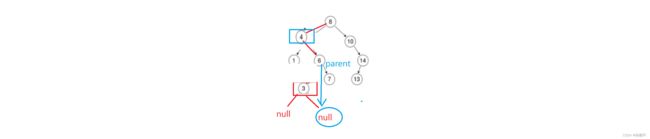
现在我们要删除3节点怎么删：
还是上面的方法，要么找右子树的最左节点（也就是右子树最小节点）或者找左子树最由节点（也就是左子树最大节点），然后进行替换。
拿找右子树的最左节点举例：
先向右走
Node* subleft = cur->_right; 
然后再判断右子树的左分支子树是否为空，不为空就往左走，走到空为止：
else
{
Node* parent = cur;
Node* subleft = cur->_right;
while (subleft->left)
{
parent = subleft;
subleft = subleft->_left;
}
}
找到节点之后进行交换：
swap(cur->_key, subLeft->_key);
if (subLeft == parent->_left)
parent->_left = subLeft->_right;
else
parent->_right = subLeft->_right;
}然后return true显示找到了值并且删除了：
return true;整个删除就结束了，如果没有找到并且删除就return fales;
return false;Erase完整code
bool Erase(const K& key)
{
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
// 准备删除 20:15继续
if (cur->_left == nullptr)
{//左为空
if (cur == _root)
{
_root = cur->_right;
}
else
{
if (cur == parent->_left)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
}
else if (cur->_right == nullptr)
{//右为空
if (cur == _root)
{
_root = cur->_left;
}
else
{
if (cur == parent->_left)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
}
else
{//左右都不为空
// 右树的最小节点(最左节点)
Node* parent = cur;
Node* subLeft = cur->_right;
while (subLeft->_left)
{
parent = subLeft;
subLeft = subLeft->_left;
}
swap(cur->_key, subLeft->_key);
if (subLeft == parent->_left)
parent->_left = subLeft->_right;
else
parent->_right = subLeft->_right;
}
return true;
}
}
return false;
}
删除一下看看：
bt.Inorder();
printf("\n");
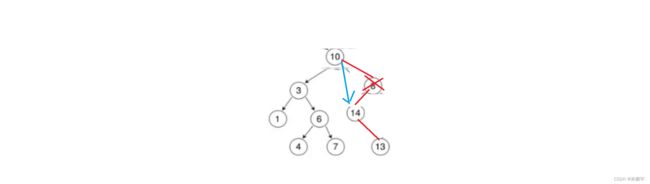
bt.Erase(3);
bt.Inorder( );
printf("\n");
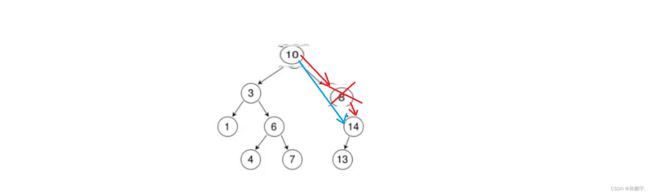
bt.Erase(14);
bt.Inorder();
printf("\n");
改
改的话目前不能改，如我们把3改为80，那就改变搜二叉的结构了：
托管代码
BinarySearchTree for version · - 开源中国 (gitee.com)