SincNet原理和代码学习

Mirco Ravanelli, Yoshua Bengio, “Speaker Recognition from raw waveform with SincNet”

1. 论文内容

• 摘要
• 介绍
• SincNet架构
• 相关工作
• 实验设置
• 结果
• 结论和展望

1）摘要

        端到端的CNN模型直接从原始语音波形学习低层次的语音表示，而不需要人工手动提取特征，这使得网络能更好地学习说话人特征(音调和共振峰)。实现这个目标的前提是正确设计神经网络的结构。文章提出一种新的CNN架构，SincNet。它要求第一卷积层学习到更有意义的滤波器，通过参数化的Sinc函数实现带通滤波。标准CNN中滤波器需要学习所有权重，而本架构中，只需要学习低截止频率和高截止频率，这提供了紧凑和有效的方法来设计定制滤波器组。在说话人识别和说话人验证任务上进行的实验表明，本文所提出的结构收敛速度更快，在原始波形上的性能均优于标准CNN。

2）介绍

        说话人识别的应用相当广泛。常用方法有传统的GMM-UBMs、目前大多数先进方案采用的i-vector表示，以及最近兴起的深度学习方法。如使用DNN在i向量表示框架中计算Baum-Welch统计量，使用DNN进行帧级特征提取，以及使用DNN直接区分说话人。然而，过去的大多数方法均使用手动提取的特征，如FBANK和MFCC系数。它们不能保证对所有语音相关任务都能达到最优。因此，可以考虑直接向模型输入时频图甚至是原始波形。CNN正是目前处理原始信号时最流行的架构，因为权重共享、局部滤波和池化能找到更加具有鲁棒性和不变性的表示。

        作者认为当前基于原始波形的CNN中，最关键的部分是第一个卷积层。它不仅要处理高维度的输入，还容易受到梯度消失的影响。CNN学习到的第一层滤波器通常呈现出有干扰且不协调的多个频带的形状，特别是遇到小样本问题时更是如此。这些滤波器对神经网络而言当然有意义，但是并不符合人类的直觉，也不能得到语音信号的有效表示。

        为了让CNN学到更具有意义的滤波器，文章对滤波器的形状进行了限制。传统的CNN中，滤波器组的所有权重都需要经过学习。SincNet则使用一组参数化的sinc函数来实现带通滤波，滤波器只需要学习低截止频率和高截止频率两个参数。这使得网络具有一定灵活性的同时，迫使网络专注于学习对滤波器形状和带宽具有巨大影响的高层次的可调参数。

3）SincNet架构

        标准CNN中，第一个卷积层将执行输入波形与FIR滤波器之间的时域卷积。卷积定义如下：

        其中，x[n]代表语音信号，h[n]代表长度为L的滤波器，y[n]代表滤波后的输出。

        标准CNN中，每个滤波器的L个权重都需要从数据中学习得来。相反地，SincNet只需要输入信号与仅有少量可学参数θ的预设函数g进行卷积，如下等式：

        受数字信号处理中标准滤波方式的启发，一种合理的选择是使用由矩形带通滤波器组成的滤波器组来定义g。频域中，带通滤波器可表示成两个低通滤波器的差：

        其中，f1和f2分别是学习得到的低截止频率和高截止频率，rect表示频域中的矩形窗。

        经过IFT转换到时域后，g表示为：

        其中，sinc函数定义为：sinc(x)=sin(x)/x

        截止频率可以在[0, fs/2]范围内随机初始化，fs代表输入信号的采样率。除此之外，也可采用梅尔尺度滤波器组的截止频率来进行初始化，其优点是在包含说话人身份关键信息的频率较低的部分设置更多滤波器。

        为确保且，上述公式中的f1和f2实际上由以下等式替换：

        需要指出的是，实际上并没有强制f2满足奈奎斯特采样定理，因为作者观察到这个限制在训练时自然满足。此外，各个滤波器在这个阶段并没有学习到增益。增益将在后续网络层学习。

        理想的带通滤波器(具有完全平坦的通带和无穷衰减的阻带)，要求滤波器权重的个数L是无限的。对g进行截断将只能得到通带具有波纹且阻带为有限衰减的近似理想滤波器。缓解这个问题的一种方法是加窗。加窗是通过将截断的g与窗函数w相乘实现的，旨在对g末尾突变的不连续点进行平滑：

        文章中采用的是Hamming窗，定义如下：

        汉明窗对频率的选择性很高。然而，结果显示使用其他窗函数时，没有显著差异。

        SincNet中涉及的所有操作都是完全可微的，且滤波器截止频率可以和其他CNN参数那样使用SGD或其他梯度优化方法进行联合优化。

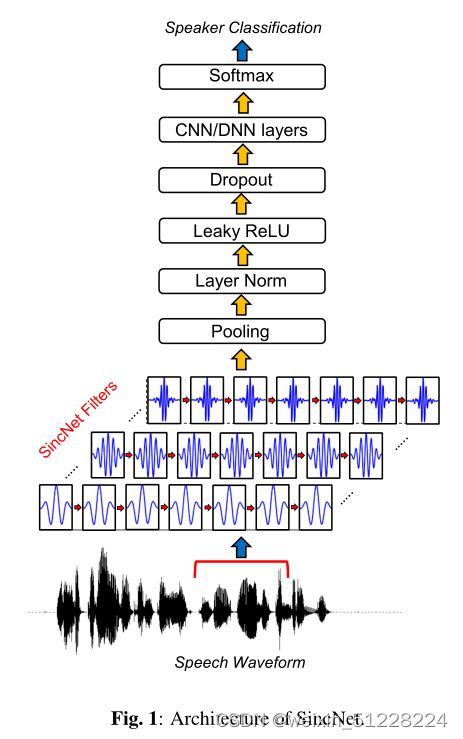
        SincNet架构：第一层为sinc卷积，紧接着是标准CNN流水线操作(池化、归一化、激活、dropout)，然后将多个标准卷积或者全连接层堆叠在一起，最后使用softmax分类器进行说话人分类。

         提出的SincNet具有以下特性：

• 收敛速度快
• 参数少
• 计算效率高
• 具有可解释性

4）相关工作

        最近的一些工作使用的低层次的语音表示来用CNN处理音频和语音信号。大多数都是用幅频特征。虽然幅频特征能比标准手工制作的特征保留更多信息，但设计时需要调整一些关键的超参数，如帧窗口的持续时间、重叠和类型以及频率区间的数量。因此，目前研究的趋势是直接从原始波形中学习，避免任何特征提取的步骤。之前的一些工作，像SincNet一样，对CNN滤波器增加约束，使它们在特定频带上工作，但它们是在频谱特征上进行处理，并且仍需要学习L个权重。比如最近提出的一种方法，使用参数化的高斯滤波器在频域上处理输入。

5）实验设置

        在两种公开语料库Librispeech和TIMIT上，对SincNet进行评估，并与其他说话人识别的基线进行比较。一种是标准CNN，一种是手动提取特征(MFCC、FBANK)的方式。对说话人验证实验还考虑了i-vector方法。

6）结果

        首先展示SincNet与标准CNN的差异。之后在说话人识别和验证的任务上将SincNet与其他方法进行了比较。

a. 滤波器分析

        标准CNN学习到的滤波器并不总是具有明确的频率响应。经常呈现出噪声或者不规则的频带形状。相反，SincNet学习到的滤波器可以明确看出，能实现矩形带通滤波，从而得到有意义的滤波器。

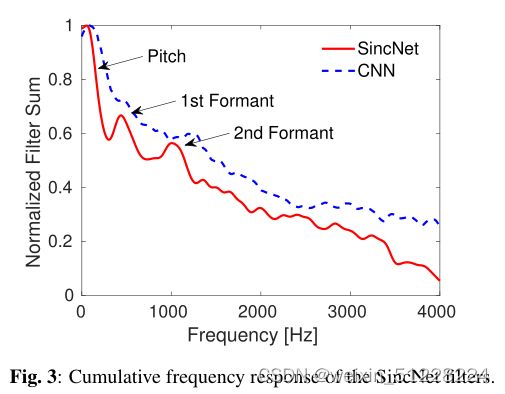
        除了对滤波器进行定性分析，更重要的一点是检查它们覆盖的频带范围。如下图展示的滤波器累计频率响应。SincNet展现出明显的三个主峰，分别代表音调(男性平均为133 Hz，女性为234 Hz)、第一共振峰(500 Hz左右，对应英语元音的平均值)以及第二共振峰(900-1400 Hz，对应元音/a/所在的1100 Hz)。该组滤波器表明，SinNet在解决说话人识别问题上成功地调整了它的特性。相反，标准CNN没有表现出这种有意义的模式，它表现出了音调，但第一共振峰和第二共振峰的位置不明显。事实证明，SincNet较标准CNN更能体现频率选择性，能更好捕捉窄带信息。

b. 说话人识别

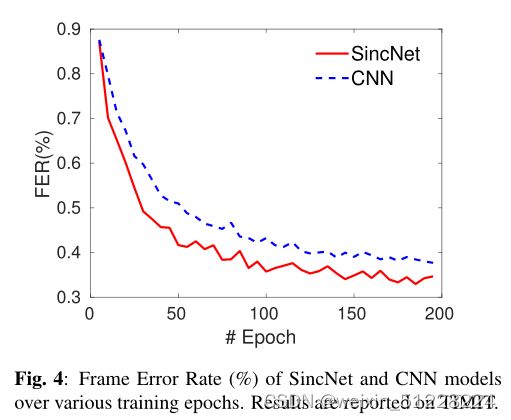
        SincNet比CNN的收敛速度更快，并且能取得更低的错误率。

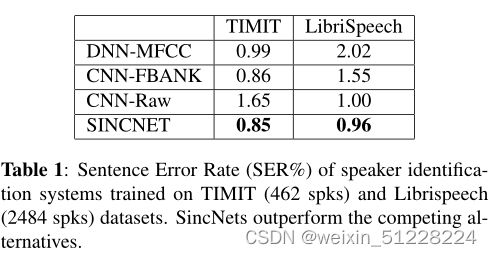
        表1显示SincNet在TIMIT和Librispeech数据集上均优于其他系统。        

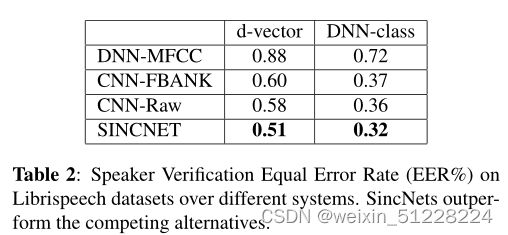
c. 说话人验证

        SincNet优于其他模型，DNN上性能更好，但DNN必须为每个新的说话人进行微调，灵活性不如d-vector。

        

2. 代码解析

class SincConv1D(Layer):
    # 初始化，定义传入该层的参数
    def __init__(
            self,
            N_filt, # 滤波器的个数
            Filt_dim, # 每个滤波器的长度
            fs, #采样频率
            **kwargs):
        self.N_filt = N_filt
        self.Filt_dim = Filt_dim
        self.fs = fs

        super(SincConv1D, self).__init__(**kwargs)

    # 因为__init__函数中有位置参数，如果不重写get_config方法将出错 
    # 如果不重写get_config,将无法在Tensorboard中载入模型图(model graph),无法使用model.save保存模型
    def get_config(self):
        return {"N_filt": self.N_filt,
                "Filt_dim": self.Filt_dim,
                "fs": self.fs}

    @classmethod
    def from_config(cls, config):
        return cls(**config)
    
    # 定义权重
    def build(self, input_shape):
        # 定义滤波器中可训练参数，即每个滤波器的起始频率和带宽
        self.filt_b1 = self.add_weight(
            name='filt_b1',
            shape=(self.N_filt,),
            initializer='uniform',
            trainable=True)
        self.filt_band = self.add_weight(
            name='filt_band',
            shape=(self.N_filt,),
            initializer='uniform',
            trainable=True)

        # 滤波器组的梅尔初始化
        low_freq_mel = 80
        high_freq_mel = (2595 * np.log10(1 + (self.fs / 2) / 700))  # 从Hz转换到梅尔刻度
        mel_points = np.linspace(low_freq_mel, high_freq_mel, self.N_filt)  # 梅尔刻度上间隔均匀的一组点
        f_cos = (700 * (10 ** (mel_points / 2595) - 1))  # 从梅尔刻度转换到Hz
        b1 = np.roll(f_cos, 1)
        b2 = np.roll(f_cos, -1)
        b1[0] = 30
        b2[-1] = (self.fs / 2) - 100
        self.freq_scale = self.fs * 1.0
        self.set_weights([b1 / self.freq_scale, (b2 - b1) / self.freq_scale]) #权重赋给filt_b1和filt_band
        
        # np.roll示例
        # >> x = np.arange(10)  
        # array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
        # >> np.roll(x, 2)  # axis为None，则会先进行扁平化，然后再向水平滚动2个位置
        # array([8, 9, 0, 1, 2, 3, 4, 5, 6, 7])
        

        # 生成汉明窗
        n = np.linspace(0, self.Filt_dim, self.Filt_dim)
        window = 0.54 - 0.46 * K.cos(2 * math.pi * n / self.Filt_dim)
        window = K.cast(window, "float32")

        # 为防止保存模型结构时出现问题，给窗函数定义特殊变量名
        self.window = K.variable(window, name='window')
        debug_print("  window", self.window.shape)

        # 矩形带通滤波器在时域上的响应为偶对称的，该变量计算滤波器一侧的点数(另一侧对称)，方便计算滤波器系数
        t_right_linspace = np.linspace(1, (self.Filt_dim - 1) / 2, int((self.Filt_dim - 1) / 2))

        # 为防止保存模型结构时出现问题，给其定义特殊变量名
        self.t_right = K.variable(t_right_linspace / self.fs, name='t_right')
        debug_print("  t_right", self.t_right)
        
        # 确保在build函数的最后调用该语句
        super(SincConv1D, self).build(input_shape) 

    def call(self, x, **kwargs):
        debug_print("call")
        # filters = K.zeros(shape=(N_filt, Filt_dim))

        # 获取滤波器的起始和截止频率，注意此处频率为归一化的模拟频率，即对采样率进行了归一化
        min_freq = 50.0
        min_band = 50.0
        self.filt_beg_freq = K.abs(self.filt_b1) + min_freq / self.freq_scale #对原始的起始频率filt_b1向右平移，确保起始频率大于50Hz
        self.filt_end_freq = self.filt_beg_freq + (K.abs(self.filt_band) + min_band / self.freq_scale) #对原始的带宽filt_band向右平移，确保带宽大于50Hz

        # 计算每个滤波器的系数，对应论文中的公式(4)，sinc函数定义见最后
        output_list = []
        for i in range(self.N_filt):
            low_pass1 = 2 * self.filt_beg_freq[i] * sinc(self.filt_beg_freq[i] * self.freq_scale, self.t_right) #
            low_pass2 = 2 * self.filt_end_freq[i] * sinc(self.filt_end_freq[i] * self.freq_scale, self.t_right)
            band_pass = (low_pass2 - low_pass1)
            band_pass = band_pass / K.max(band_pass)
            output_list.append(band_pass * self.window)
        filters = K.stack(output_list)  # (80, 251)
        filters = K.transpose(filters)  # (251, 80)
        filters = K.reshape(filters, (self.Filt_dim, 1,
                                      self.N_filt))  # (251,1,80) 
        # TF: (filter_width, in_channels, out_channels) 
        # PyTorch: (out_channels, in_channels, filter_width)

        '''Given an input tensor of shape [batch, in_width, in_channels] if data_format is "NWC", or [batch, 
        in_channels, in_width] if data_format is "NCW", and a filter / kernel tensor of shape [filter_width, 
        in_channels, out_channels], this op reshapes the arguments to pass them to conv2d to perform the equivalent 
        convolution operation. Internally, this op reshapes the input tensors and invokes tf.nn.conv2d. For example, 
        if data_format does not start with "NC", a tensor of shape [batch, in_width, in_channels] is reshaped to [
        batch, 1, in_width, in_channels], and the filter is reshaped to [1, filter_width, in_channels, out_channels]. 
        The result is then reshaped back to [batch, out_width, out_channels] (where out_width is a function of the 
        stride and padding as in conv2d) and returned to the caller. '''

        # 实现卷积
        debug_print("call")
        debug_print("  x", x)
        debug_print("  filters", filters)
        out = K.conv1d(
            x,
            kernel=filters
        )
        debug_print("  out", out)

        return out

    # 计算输出维度
    def compute_output_shape(self, input_shape):
        new_size = conv_utils.conv_output_length(
            input_shape[1],
            self.Filt_dim,
            padding="valid",
            stride=1,
            dilation=1)
        return (input_shape[0],) + (new_size,) + (self.N_filt,)


# 在类的外部定义变量，来防止出现以下错误
# 'ValueError: A tf.Variable created inside your tf.function has been garbage-collected.'
v = K.variable(K.ones(1))
def sinc(band, t_right):
    y_right = K.sin(2 * math.pi * band * t_right) / (2 * math.pi * band * t_right)
    # y_left = flip(y_right, 0) TODO remove if useless
    y_left = K.reverse(y_right, 0)
    y = K.concatenate([y_left, v, y_right])
    return y

keras中编写自定义层只需要实现以下三个方法:

• build(input_shape): 这是定义权重的地方。这个方法必须设 self.built = True，可以通过调用 super([Layer], self).build() 完成。
• call(x): 这里是编写层的功能逻辑的地方。只需要关注传入 call 的第一个参数：输入张量，除非你希望你的层支持masking。
• compute_output_shape(input_shape): 如果你的层更改了输入张量的形状，你应该在这里定义形状变化的逻辑，这让Keras能够自动推断各层的形状。