2023和鲸夏令营创作活动【黄金价格分析预测】
2023和鲸夏令营创作活动【黄金价格分析预测】
文章目录
- 2023和鲸夏令营创作活动【黄金价格分析预测】
-
- 一、项目背景
- 二、数据说明
- 三、数据预处理
- 四、数据探索性分析
- 五、构建LSTM模型预测
-
- 1、构建LSTM模型
- 2、绘制loss的变化曲线
- 3、进行预测
一、项目背景
本项目的目标是分析并预测2012年至2022年的黄金成交价格。我们将使用时间序列数据,并采用LSTM模型进行预测。
二、数据说明
数据集包含以下字段:
- Date:日期
- Close/Last:收盘价
- Volume:成交量
- Open:开盘价
- High:最高价
- Low:最低价
数据缺失情况如下:
- Date:0
- Close/Last:0
- Volume:39
- Open:0
- High:0
- Low:0
在接下来的分析中,我们将首先进行数据探索性分析和可视化,然后使用LSTM模型进行预测,并对预测结果进行可视化。
三、数据预处理
在进行数据分析之前,我们需要对数据进行预处理。这包括处理缺失值,转换数据类型等。
import pandas as pd
df = pd.read_csv('gold_data.csv')
df.head()
# 查看数据信息,包括每列的数据类型和非空值数量
df.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 2547 entries, 0 to 2546
Data columns (total 6 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Date 2547 non-null object
1 Close/Last 2547 non-null float64
2 Volume 2508 non-null float64
3 Open 2547 non-null float64
4 High 2547 non-null float64
5 Low 2547 non-null float64
dtypes: float64(5), object(1)
memory usage: 119.5+ KB
从上述信息中,我们可以看到,数据集中有2547条记录,其中’Volume’列有39个缺失值。'Date’列的数据类型为object,我们需要将其转换为datetime类型以便进行时间序列分析。
# 处理缺失值
# 由于Volume列存在缺失值,我们选择使用前一天的Volume值进行填充
df['Volume'].fillna(method='ffill', inplace=True)
# 将Date列的数据类型转换为datetime
df['Date'] = pd.to_datetime(df['Date'])
# 再次查看数据信息
df.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 2547 entries, 0 to 2546
Data columns (total 6 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Date 2547 non-null datetime64[ns]
1 Close/Last 2547 non-null float64
2 Volume 2547 non-null float64
3 Open 2547 non-null float64
4 High 2547 non-null float64
5 Low 2547 non-null float64
dtypes: datetime64[ns](1), float64(5)
memory usage: 119.5 KB
四、数据探索性分析
在进行预测之前,我们先对数据进行探索性分析,以了解数据的基本情况。
import pyecharts.options as opts
from pyecharts.charts import Line
# 绘制收盘价的时间序列图
line = (
Line(init_opts=opts.InitOpts(width="800px", height="400px"))
.add_xaxis(df['Date'].tolist())
.add_yaxis("Close/Last Price", df['Close/Last'].tolist())
.set_series_opts(label_opts=opts.LabelOpts(is_show=False))
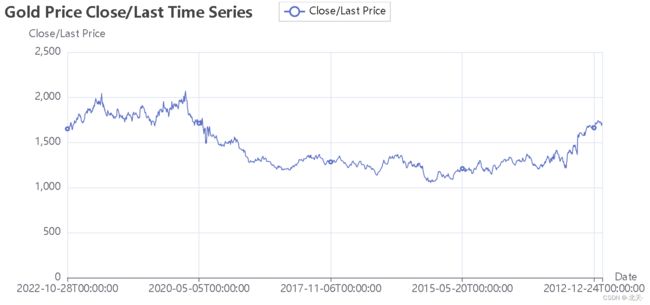
.set_global_opts(title_opts=opts.TitleOpts(title="Gold Price Close/Last Time Series"),
xaxis_opts=opts.AxisOpts(name="Date"),
yaxis_opts=opts.AxisOpts(name="Close/Last Price"))
)
line.render_notebook()
从上图我们可以看出,黄金的收盘价在2012年至2022年期间总体上呈现出上升的趋势,但在某些时间段内也出现了波动。这种时间序列的特性使得我们可以使用LSTM模型进行预测。
五、构建LSTM模型预测
接下来,我们将使用LSTM模型对黄金价格进行预测。
1、构建LSTM模型
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import train_test_split
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
# 数据归一化
scaler = MinMaxScaler(feature_range=(-1, 1))
data = scaler.fit_transform(df['Close/Last'].values.reshape(-1, 1))
# 划分训练集和测试集
train_data, test_data = train_test_split(data, test_size=0.2, shuffle=False)
# 转换为tensor
train_data = torch.FloatTensor(train_data).cuda()
test_data = torch.FloatTensor(test_data).cuda()
# 定义LSTM模型
class LSTM(nn.Module):
def __init__(self, input_size=1, hidden_layer_size=200, output_size=1):
super().__init__()
self.hidden_layer_size = hidden_layer_size
self.lstm = nn.LSTM(input_size, hidden_layer_size)
self.linear = nn.Linear(hidden_layer_size, output_size)
self.hidden_cell = (torch.zeros(1,1,self.hidden_layer_size).cuda(),
torch.zeros(1,1,self.hidden_layer_size).cuda())
def forward(self, input_seq):
lstm_out, self.hidden_cell = self.lstm(input_seq.view(len(input_seq) ,1, -1), self.hidden_cell)
predictions = self.linear(lstm_out.view(len(input_seq), -1))
return predictions[-1]
# 训练模型
model = LSTM().cuda()
loss_function = nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
epochs = 100
losses = []
for i in range(epochs):
for seq in train_data:
optimizer.zero_grad()
model.hidden_cell = (torch.zeros(1, 1, model.hidden_layer_size).cuda(),
torch.zeros(1, 1, model.hidden_layer_size).cuda())
y_pred = model(seq)
single_loss = loss_function(y_pred, seq)
single_loss.backward()
optimizer.step()
losses.append(single_loss.item())
if i%25 == 1:
print(f'epoch: {i:3} loss: {single_loss.item():10.8f}')
print(f'epoch: {i:3} loss: {single_loss.item():10.10f}')
epoch: 1 loss: 0.00053112
epoch: 26 loss: 0.00000370
epoch: 51 loss: 0.00000417
epoch: 76 loss: 0.00000103
epoch: 99 loss: 0.0000000606
2、绘制loss的变化曲线
# 绘制loss的变化曲线
line = (
Line(init_opts=opts.InitOpts(width="800px", height="400px"))
.add_xaxis(range(epochs))
.add_yaxis("Loss", losses)
.set_series_opts(label_opts=opts.LabelOpts(is_show=False))
.set_global_opts(title_opts=opts.TitleOpts(title="Loss Curve"),
xaxis_opts=opts.AxisOpts(name="Epoch"),
yaxis_opts=opts.AxisOpts(name="Loss"))
)
line.render_notebook()
3、进行预测
import numpy as np
# 使用训练好的模型进行预测
model.eval()
test_inputs = train_data[-100:].tolist()
test_outputs = []
for i in range(len(test_data)):
seq = torch.FloatTensor(test_inputs[-100:]).cuda()
with torch.no_grad():
model.hidden = (torch.zeros(1, 1, model.hidden_layer_size).cuda(),
torch.zeros(1, 1, model.hidden_layer_size).cuda)
test_inputs.append(test_data[i])
test_outputs.append(model(seq).item())
# 反归一化
predicted_price = scaler.inverse_transform(np.array(test_outputs).reshape(-1, 1))
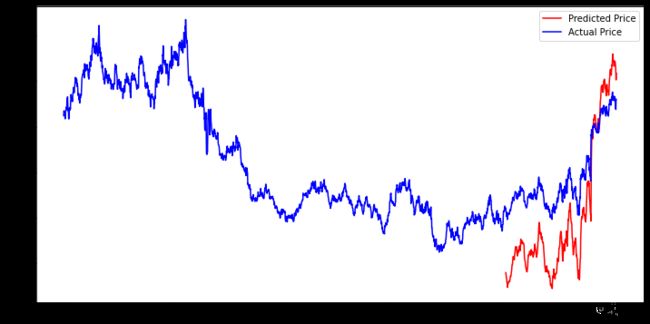
# 绘制预测结果
plt.figure(figsize=(12, 6))
plt.plot(range(len(train_data), len(train_data) + len(predicted_price)), predicted_price, color='r', label='Predicted Price')
plt.plot(range(len(data)), scaler.inverse_transform(data), color='b', label='Actual Price')
plt.legend()
plt.show()
# 打印预测准确率
print('预测准确率:', 1 - np.mean(np.abs((predicted_price - scaler.inverse_transform(data[len(train_data):])) / scaler.inverse_transform(data[len(train_data):]))))
预测准确率: 0.8444566607225441