算法通过村第十七关-贪心|青铜笔记|贪心也很简单呕
文章目录
- 前言
- 难以解释的贪心算法
- 贪心问题
-
- 发放饼干
- 柠檬水找零
- 分发糖果
- 总结
前言
提示:我像接纳变甜的果实一般迎接此时。 --朱塞培·翁加雷蒂《享受》
贪心的思想很难用理论去解释,这里我们通过案例感受下,怎么思考贪心的问题。
难以解释的贪心算法
真的很难说清楚贪心的道理,越是用权威的语言越是晦涩难懂。做题的时候怎么快速定位,并且做出来呢?
如果非要你解释以下,你会不会反而更加懵呢☠️?
更让人恼火的是贪心的题目没有什么固定的套路,一个题目一个方式,好在大部分的贪心算法不是特别的难,因此公认的贪心学习法则是“直接做题目,不要先考虑谈不贪心哈”。说了这么多,我们就来看一些经典的题目,去寻找一些“哲学规律”吧。
贪婪算法(贪心)是指:在对于问题进行求解是,在每一步先择中采取最好或者最优(即有利)的选择,从而希望能够导致结果是最好或者最优的算法;贪婪算法所得到的结果补一点给是最优的结果(当然有时侯会是最优解嘛)但是都是相对接近最优解的结果。
那贪婪是否可以直接得到最优解呢?《算法导论》中给出了答案:贪婪算法不能保证一定能得到最优解,但是对很多问题确实可以得到最优解。
这里似乎有些矛盾,很难考究,并不是特别明确,大部分的解释其实就是看上就也就这样啦。
还有一个问题:什么时候该用贪心呢?
这要求要解决的题目具有很好的“最优子结构”,->这里怎么说呢? 就好像说用高等数学证明“1 + 1 = 2”.解释不如不解释。
既然贪心如此邪门,那我们该如何下手呢?这里总结一些常见的经典场景,看看贪心出题大概是什么方向,什么样子的,面试做到心里有数哈。
举例说明:
- 排序问题:选择排序、拓扑排序
- 优先队列:堆排序
- 赫夫曼压缩编码
- 图:Prim、Fruskall、Dijkstra算法
- 硬币找零问题
- 分数背包问题
- 并查集的按大小或者高度合并问题或者排名
- 任务调度问题
- 一些复杂问题的近似算法
所以贪婪我觉得更贴切,我们应该像打太极一样,以无招胜有招对待它。具体根据题目特点,直接该怎么做就怎么做哈
贪心问题
发放饼干


这里既要满足小孩的胃口,也不要造成饼干的尺寸浪费。大尺寸的饼干既可以满足胃口大的孩子也可以满足胃口小的孩子,那么就优先满足胃口大的,这里的局部优先就是先用大饼干喂饱胃口大的,充分利用饼干尺寸,喂饱一个,全局优先就是尽量喂饱可能多的小孩。
所以:这里可以使用贪婪的策略,先将饼干数组和小孩数组排序,然后从后先前遍历小孩数组,用大饼干优先满足胃口大的,并统计小孩数量就可以了。代码这样:
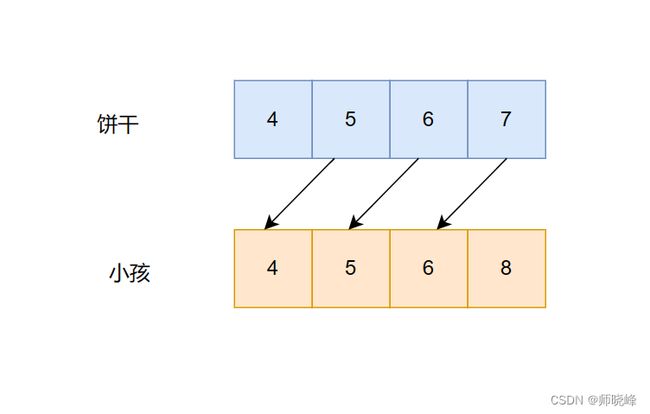
这里我们就优先考虑胃口,大饼干先喂饱大胃口,最后看有几个孩子可以满足就行了。
/**
* 分发饼干
* @param g
* @param s
* @return
*/
public static int findContentChildren(int[] g, int[] s) {
Arrays.sort(g);
Arrays.sort(s);
int start = s.length - 1;
int count = 0;
// 遍历孩子看是否满足
int index;
for(index = g.length - 1; index >= 0; index--) {
if (start >= 0 && g[index] <= s[start]) {
count++;
start--;
}
}
return count;
}
柠檬水找零
参考题目介绍:860. 柠檬水找零 - 力扣(LeetCode)


这个题目换个理解是这样的:如果是小孩子的话更简单,参在下面三种情况
- 如果是5,直接收下
- 如果是10,收下10,找5(此时必须有5
- 如果是20,收下20,要么找10和5,要么给三个5(假设有的话)
当然上面的情况(有10 给10 没10 给5)的原则。这也是贪婪的选择过程。为什么要优先消耗10呢?因为5的用处更大不是嘛哈哈。
这里也是局部最优解推至全局最优解:
代码:
public boolean lemonadeChange(int[] bills) {
// 表示5和10的数量
int count_5 = 0;
int count_10 = 0;
for (int i = 0; i < bills.length; i++) {
if (bills[i] == 5) {
count_5++;
}
if (bills[i] == 10) {
count_5--;
count_10++;
}
if (bills[i] == 20) {
if (count_10 > 0) {
count_10--;
count_5--;
} else {
count_5 -= 3;
}
}
if (count_5 < 0 || count_10 < 0){
return false;
}
}
return true;
}
分发糖果
参考题目地址:135. 分发糖果 - 力扣(LeetCode)


首先我们看来这个题目有点意思的,假如有5个孩子,因为每个孩子至少一个糖果,所以一定要花费出去5个{1,1,1,1,1}.✅
然后是相邻的孩子评分高的获得更多的糖果。假如评分为{1,2,3,2},则最少花出去的糖果为{1,2,3,1},因为前三个评分在增加嘛,那么糖果也在增加。因此分别要发的糖果最少为{1,2,3},最后一个评分低,我们至少给1个对吧。
当然会出现极端的情况:评分相同例如{1,2,2,2,2},根据题目要求重复的给一个就可以了,也就是说{1,2,1,1,1}.
首先,我们更具提议从左向右依次比较,确定第一轮要预发的糖果数量,只要右边的比左边大,就一直加1;如果右边比左边小,就设置1,然后继续向右比较,结果是这样的:
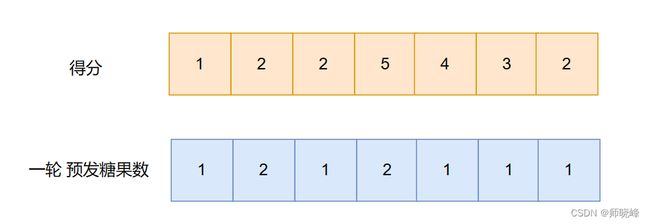
注意此时还不是最终答案,根据题目要求相邻的孩子评分高的必须获取更多糖果,结果并不一致。
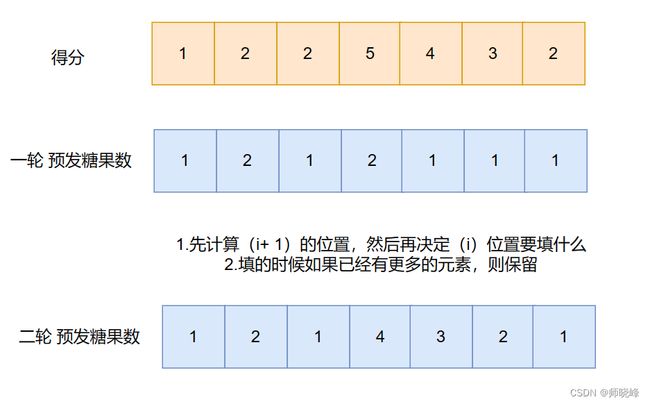
所以就有了第二轮的发放糖果,再从右向左走。如果左边的比右边小,则不做处理,如果左边的比右边大,则不是简单的加1,而是在{i+ 1}的基础上,先加1 在复制给{i}。
看图说话:
例如最后四个评委的评分为{5,4,3,2},一轮结束后{2,1,1,1}.
如果我们只只考虑从右到左的时候,很显然:
- 最后第一个得到的是1个糖果
- 最后第二个得到的是2个糖果
- 最后第三个得到的是3个糖果
- 最后第四个得到的是4个糖果
因此最后四个的right={4,3,2,1},接下来每个位置i我们只要从left[i]和right[i]中先择最大的就行了,只不过这里我们其实不用两个数组,一个数组更新两次就可以了,首先从左向右给预发一轮糖果,然后再从右向左更新数组元素,每次赋值钱比较取最大的一个即可。
/**
* 分发糖果
* @param ratings
* @return
*/
public static int candy(int[] ratings) {
int len = ratings.length;
int[] candyValues = new int[len];
// 技巧1 从1开始
candyValues[0] = 1;
for (int i = 1; i < len; i++) {
//从左向右比较
if (ratings[i] > ratings[i - 1]){
candyValues[i] = candyValues[i - 1] + 1;
}else{
candyValues[i] = 1;
}
}
// 反序
// 技巧2 从倒数第二个开始
for (int i = len - 2; i >= 0; i--) {
if (ratings[i] > ratings[i + 1]){
candyValues[i] = Math.max(candyValues[i],candyValues[i+ 1] + 1);
}
}
int ans = 0;
for(int s : candyValues){
ans += s;
}
return ans;
}
总结
提示:贪婪算法核心;贪婪的例子入门;典型的折磨;琢磨不透哦;逻辑总结
如果有帮助到你,请给题解点个赞和收藏,让更多的人看到 ~ ("▔□▔)/
如有不理解的地方,欢迎你在评论区给我留言,我都会逐一回复 ~
也欢迎你 关注我 ,喜欢交朋友,喜欢一起探讨问题。
