支持向量机（Support Vector Machine，SVM）

声明：来源https://blog.csdn.net/xiaowei_cqu/article/details/35993729，

（个人感觉博主xiaowei_cqu很多博文写的都不错，值得学习）

另外，关于SVM和核函数的介绍还可以参考：

https://blog.csdn.net/batuwuhanpei/article/details/52354822

https://blog.csdn.net/bitcarmanlee/article/details/77604484

一、SVM简介

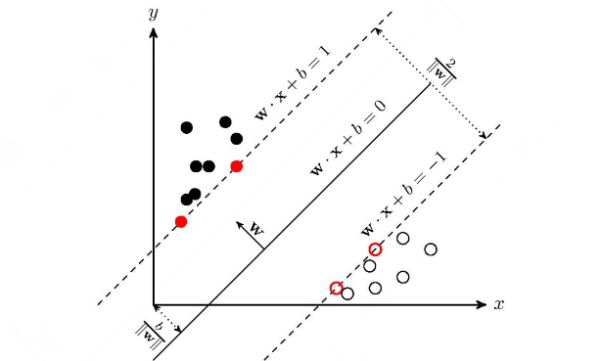
       SVM是由Vanpik领导的AT&TBell实验室研究小组，在1963年提出的一种新的非常有潜力的分类技术, SVM是一种基于统计学习理论的模式识别方法，主要应用于模式识别领域。它是一种以统计学理论为基础的，以结构风险最小化的学习机学习方法，在解决小样本 、非线性及高维模式识别问题中表现出许多特有的优势,并能够推广应用到函数拟合等其他机器学习问题中。SVM的关键在于核函数，可以将低维空间中难于划分的向量映射到高维空间。但这个办法带来的困难就是计算复杂度的增加，而核函数正好巧妙地解决了这个问题。

常调节参数c和g，二者的具体含义如下：

C是惩罚系数，理解为调节优化方向中两个指标（间隔大小，分类准确度）偏好的权重，即对误差的宽容度，C越高，说明越不能容忍出现误差,容易过拟合，C越小，容易欠拟合，C过大或过小，泛化能力变差。

g（gamma）是选择RBF函数作为kernel后，该函数自带的一个参数。隐含地决定了数据映射到新的特征空间后的分布，gamma越大，支持向量越少，gamma值越小，支持向量越多。支持向量的个数影响训练与预测的速度。

二、核函数

       SVM核函数的选择对于其性能的表现有至关重要的作用，尤其是针对那些线性不可分的数据，因此核函数的选择在SVM算法中就显得至关重要。对于核技巧我们知道，其目的是希望通过将输入空间内线性不可分的数据映射到一个高纬的特征空间内使得数据在特征空间内是可分的，我们定义这种映射为ϕ(x)ϕ(x)，那么我们就可以把求解最大化分类间隔，转化为求解约束最优化问题，即为：
minαs.t.αi≥0,12∑Ni=1∑Nj=1αiαjyiyj(ϕi⋅ϕj)−∑Ni=1αi∑Ni=1αiyi=0i=1,2,...,N
minα12∑i=1N∑j=1Nαiαjyiyj(ϕi⋅ϕj)−∑i=1Nαis.t.∑i=1Nαiyi=0αi≥0,i=1,2,...,N

       但是由于从输入空间到特征空间的这种映射会使得维度发生爆炸式的增长，因此上述约束问题中内积ϕi⋅ϕjϕi⋅ϕj的运算会非常的大以至于无法承受，因此通常我们会构造一个核函数
κ(xi,xj)=ϕ(xi)⋅ϕ(xj)
κ(xi,xj)=ϕ(xi)⋅ϕ(xj)
       从而避免了在特征空间内的运算，只需要在输入空间内就可以进行特征空间的内积运算。通过上面的描述我们知道要想构造核函数κκ，我们首先要确定输入空间到特征空间的映射，但是如果想要知道输入空间到映射空间的映射，我们需要明确输入空间内数据的分布情况，但大多数情况下，我们并不知道自己所处理的数据的具体分布，故一般很难构造出完全符合输入空间的核函数，因此我们常用如下几种常用的核函数来代替自己构造核函数：
（1）线性核函数 ：
线性核，主要用于线性可分的情况，我们可以看到特征空间到输入空间的维度是一样的，其参数少速度快，对于线性可分数据，其分类效果很理想，因此我们通常首先尝试用线性核函数来做分类，看看效果如何，如果不行再换别的
（2）多项式核函数 
κ(x,xi)=((x⋅xi)+1)d
κ(x,xi)=((x⋅xi)+1)d
        多项式核函数可以实现将低维的输入空间映射到高纬的特征空间，但是多项式核函数的参数多，当多项式的阶数比较高的时候，核矩阵的元素值将趋于无穷大或者无穷小，计算复杂度会大到无法计算。
（3）高斯（RBF）核函数 
κ(x,xi)=exp(−||x−xi||2δ2)
κ(x,xi)=exp(−||x−xi||2δ2)
      高斯径向基函数是一种局部性强的核函数，其可以将一个样本映射到一个更高维的空间内，该核函数是应用最广的一个，无论大样本还是小样本都有比较好的性能，而且其相对于多项式核函数参数要少，因此大多数情况下在不知道用什么核函数的时候，优先使用高斯核函数。
（4）sigmoid核函数 
κ(x,xi)=tanh(η+θ)
κ(x,xi)=tanh(η+θ)
采用sigmoid核函数，支持向量机实现的就是一种多层神经网络。
因此，在选用核函数的时候，如果我们对我们的数据有一定的先验知识，就利用先验来选择符合数据分布的核函数；如果不知道的话，通常使用交叉验证的方法，来试用不同的核函数，误差最下的即为效果最好的核函数，或者也可以将多个核函数结合起来，形成混合核函数。在吴恩达的课上，也曾经给出过一系列的选择核函数的方法：

如果特征的数量大到和样本数量差不多，则选用线性核的SVM；
如果特征的数量小，样本的数量正常，则选用SVM+高斯核函数；
如果特征的数量小，而样本的数量很大，则需要手工添加一些特征从而变成第一种情况。

注：以上请直接参考原文https://blog.csdn.net/batuwuhanpei/article/details/52354822
 ———————————————— 

 

以下是几种常用的核函数表示：

线性核（Linear Kernel）

多项式核（Polynomial Kernel）

径向基核函数（Radial Basis Function）

也叫高斯核（Gaussian Kernel），因为可以看成如下核函数的领一个种形式：

注意：径向基函数是指取值仅仅依赖于特定点距离的实值函数，也就是，任意一个满足特性的函数 Φ都叫做径向量函数，标准的一般使用欧氏距离，尽管其他距离函数也是可以的。所以另外两个比较常用的核函数，幂指数核，拉普拉斯核也属于径向基核函数。此外不太常用的径向基核还有ANOVA核，二次有理核，多元二次核，逆多元二次核。
幂指数核（Exponential Kernel）
 
拉普拉斯核（Laplacian Kernel）
 
ANOVA核（ANOVA Kernel）
 
二次有理核（Rational Quadratic Kernel）
 
多元二次核（Multiquadric Kernel）
 
逆多元二次核（Inverse Multiquadric Kernel）
 
另外一个简单实用的是Sigmoid核（Sigmoid Kernel）
 
以上几种是比较常用的，大部分在SVM，SVM-light以及RankSVM中可用参数直接设置。还有其他一些不常用的，如小波核，贝叶斯核。