一、引述-二叉查找树
红黑树(Red Black Tree) 一种特殊的二叉查找树。故先查看二叉查找树
二叉查找树特性:左字数上所有的节点的值都小于或等于他的根节点上的值
右子树上所有节点的值均大于或等于他的根节点的值
左、右子树也跟别为平衡二叉树
1.1、示例
一个基本的二叉查找树
需求查找数据10,
第一步,查看根节点9,命中节点9
第二步,10>9,在根节点9的右侧,命中13
第三步,13>10,在节点13的左侧,命中11
第四部,11>10,在节点11的左侧,命中10
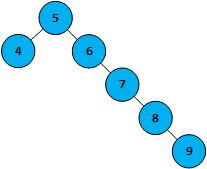
不过二叉查找树有一些问题,可能会出现不平横的情况,即如下图所示的情况
从这种情况可以看出,明显存在左子树和右子树深度相差过多,在使用平衡情况下的二叉查找树是时间复杂度为logn,而出现这种极端情况的话,想要查9的位置就需要每一次都遍历下一个右子树,很有可能时间复杂度变为n(与数组普通查询的时间复杂度相同)
基于上述情况,引入了平衡二叉树,红黑树即为平衡二叉树的一种
二、红黑树概述
红黑树(Red Black Tree) 是一种自平衡二叉查找树。别名:对称二叉B树、
红黑树和AVL树类似,都是在进行插入和删除操作时通过特定操作保持二叉查找树的平衡,从而获得较高的查找性能。
它虽然是复杂的,但它的最坏情况运行时间也是非常良好的,并且在实践中是高效的: 它可以在O(log n)时间内做查找,插入和删除,这里的n 是树中元素的数目。
2.1、数据结构
它的统计性能要好于平衡二叉树(有些书籍根据作者姓名,Adelson-Velskii和Landis,将其称为AVL-树),因此,红黑树在很多地方都有应用。在C++ STL中,很多部分(包括set, multiset, map, multimap)应用了红黑树的变体(SGI STL中的红黑树有一些变化,这些修改提供了更好的性能,以及对set操作的支持)。其他平衡树还有:AVL,SBT,伸展树,TREAP 等等。
2.2、树的旋转
2.2.1、左旋
左旋的过程是将x的右子树绕x逆时针旋转,使得x的右子树成为x的父亲,同时修改相关节点的引用。旋转之后,二叉查找树的属性仍然满足。
2.2.2、右旋
右旋的过程是将x的左子树绕x顺时针旋转,使得x的左子树成为x的父亲,同时修改相关节点的引用。旋转之后,二叉查找树的属性仍然满足。
2.2.3、小结
无论是左旋还是右旋,被旋转的树,在旋转前是二叉查找树,并且旋转之后仍然是一颗二叉查找树。
2.4、示例
1、基础示例
示例一、向红黑树中插入节点14(一般默认插入节点是红色的)
示例二、在原树上插入20
可以看到,插入以后树已经不是一个平衡的二叉树,而且并不满足红黑树的要求,因为20和21均为红色,这种情况下就需要对红黑树进行变色,21需要变为黑色,22就会变成红色,如果22变成红色,则需要17和25都变成黑色
而17变成黑色显然是不成立的,因为如果17变为黑色,那么13就会变为红色,不满足二叉树的规则,因此此处需要进行另一个操作---------左旋操作
以节点17进行左旋操作
对于上图由于右子树中17变为黑色以后需要把13变成红色,因此进行一次左旋,将17放在根节点,这样既可保证13为红色,左旋后结果
而后根据红黑树的要求进行颜色的修改
进行左旋后,发现从根节点17,到1左子树的叶子节点经过了两个黑节点,而到6的左叶子节点或者右叶子节点要经历3个黑节点,很显然也不满足红黑树,因此还需要进行下一步操作,需要进行右旋操作
以节点13进行右旋
由于是从13节点出现的不平衡,因此对13节点进行右旋,得到结果
而后再对其节点进行变色,得到结
这便是红黑树的一个变换,它主要用途有很多,例如java中的TreeMap以及JDK1.8以后的HashMap在当个节点中链表长度大于8时都会用到。
代码地址:地址 中的data-004-tree中 RBTree
参看地址:
https://www.cnblogs.com/CarpenterLee/p/5503882.html
http://www.cnblogs.com/skywang12345/p/3624343.html