14. 机器学习 - KNN & 贝叶斯
Hi,你好。我是茶桁。
咱们之前几节课的内容,从线性回归开始到最后讲到了数据集的处理。还有最后补充了SOFTMAX。
这些东西,都挺零碎的,但是又有着相互之间的关系,并且也都蛮重要的。并且是在学习机器学习过程当中比较容易忽视的一些内容。
从这节课开始呢,我要跟大家将一些其他的内容。
虽然最近几年用到的方法主要都是深度学习的方法,但是机器学习并不代表就只有深度学习这一种方法。
当然现在的深度学习其实是从线性回归演化来的,都是用一种梯度下降的方式来做。但是呢其实有很多机器学习方法用的不是这种思想。
那接下来就给大家要讲的,就是曾经非常有名,也非常有用的一些方法。这些方法的思想和用法和线性回归的机器学习不太一样。
为什么咱们现在主要用深度学习呢?之所以深度学习很火,原因就是我们的整个机器学习的模型可以像搭乐高积木一样。
比方有一个线性变化,是sigmoid,然后有一个Softmax,还有之后大家要学到什么LSTM,RNCN,还有Linear regression。他可以互相去连接,可以像玩乐高积木或者说像做电路一样,可以做出来非常复杂的模型。
那么深度学习的模型变得极其复杂之后,上节课我讲过,如果模型特别复杂,可以表证比较复杂的情况,但是需要比较多的数据去拟合它。
如果模型很复杂,就需要比较多的数据。而在现在,最近十几年互联网产生的数据量啊大了很多,所以深度学习这种复杂模型的特点就可以被释放出来了。
而在以前数据量特别小,类似深度学习这种方法,参数也特别多,效果不太好。
那我们为什么要去学习这些老的经典的学习方法的原因,就是咱们有些时候经常会遇到一个情况就是训练数据其实没有那么多,可能也就一两千个,或者说三五千个。就这几千几万个数据,用深度学习模型其实它是很复杂的,效果也不好。因为模型太复杂了,需要的数据比较多。
所以,当数据量比较小的时候,问题比较简单的时候,其实用一些比较经典的方法是比较好的。
第二个原因,像贝叶斯、KNN、还有决策树,这些方法现在虽然慢慢不是主流了,但是他背后的思想其实可以帮助我们做很多事情。
假如说要判断物体是不是相似等等类似的这些情况,这些方法可以很好的启发你。可以去用在其他场景下去解决问题。
第三个原因,传统的机器学习有比较好的可解释性。函数f(x)到底是怎么样求得的y,里边的每一步可以解释的很清楚。
举个例子,现在我们给任何一个人一台计算机,只要给足够的时间,也不用多就一个月,用深度学习模型去做股市的预测,都可以拟合一个函数拟合这个股市的预测程度非常高。
按照这个做法来做的话,我们去股市投一年可以赚200%。但是你用这个模型去预测未来的时候就不行了。
就是你去预测过去的事情,做训练可以用,不代表未来也可以用。
所以巴菲特如果问你,为啥这个东西可以?你说因为我在收集到的历史数据上做的效果比较好。你觉得巴菲特会信你吗?
但是老一代的机械学习模型,尤其是KNN、贝叶斯,可以把它的决策逻辑,为什么决策,为什么得到这个结果的过程给大家讲清楚。
除此之外要说的是,如果你想成为一个技术很厉害的技术达人,或者一个技术专家,那你要注意一件事,心态一定要开放。
深度学习不能从逻辑上解释,只能凭感觉去解释,就是只能人去解释。
就好比一个占卜的人去解释,只能靠人去去阐述。就好比牧师去解读圣经一样。科学的尽头都是玄学是吧?
之前给大家说过监督学习,监督学习有一个比较数学,比较形式化的定义:
对于一些数据,如上图,数据D={D1, D2, …, Dn}。对于这些数据有x和y,y就是它label,是desire的output,是期望的输出。
然后我们希望能够学习到一种映射,f:x -> y, 从x能够到y,只要能够实现从x到y这样的一种映射,那么它就是一种监督学习。
如果这个y输出是连续的,那么它就是回归。如果它是discrete, 那么我们就说它是分类。
所以这个mapping,这种映射关系可以是各种各样的一种映射关系,可以是很多种。
KNN
我们现在要来讲的,就是第一种。除了深度学习,线性回归和逻辑回归之外,咱们要讲的第一种,就是KNN,又称K近临。
KNN几乎可以说是最简单、最直接、最古老的一种机器学习方法了。
他的原理很简单。
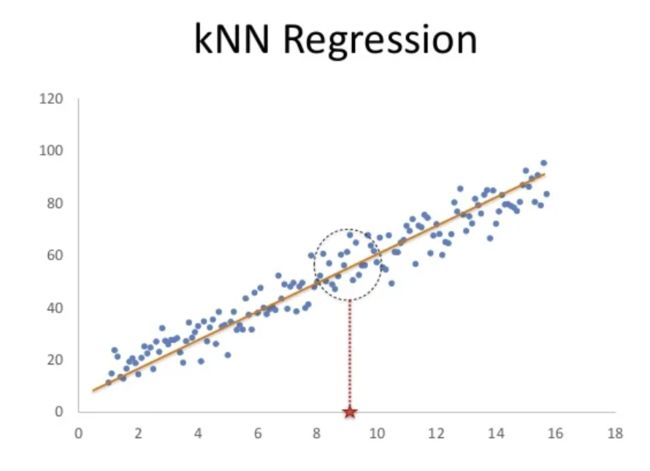
比方说我们现在有这么些点,然后问X轴红色五角星的位置向上对应的点在什么位置?
那KNN无法告诉你准确的这个点的位置是多少,但是我们可以利用周围确定的点,也就是圆圈圈定的范围内的这些点,用它们来求一个平均值。
也就是说,离的最近的k个值是多少,然后求个平均值就行了。这个好像很有道理的样子。
好,那我们看到,这个其实是解决了回归问题。那现在我们来看看分类问题:
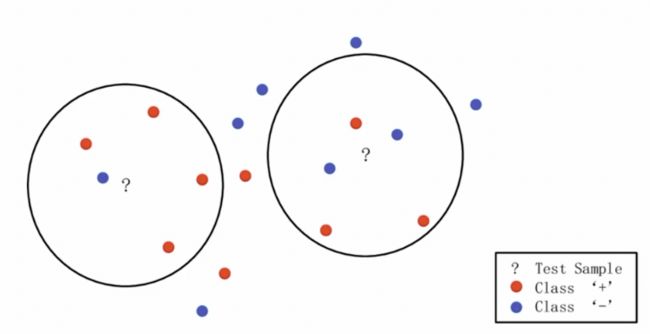
比方说上面这张图,有一些红色的点和一些蓝色的点。那么现在问题就是,?号所在的这些点是什么呢?
那左边的圈里,离的最近的是一个蓝色,四个红色,那?的这个点就是红色。在右边的这个圈里,红色比蓝色更多,那这个点也是红色。
这样的话,你会发现整个求解起来就很简单。
假如咱们给一组数据x,
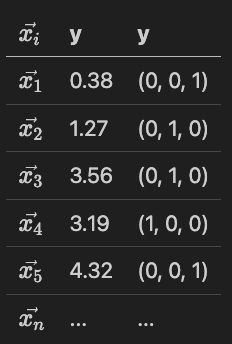
那么我们有一组 x i x_i xi, y有可能是Numerical, 也有可能是一个类别。
现在来了一个新的 x i x_i xi, 假如要知道他的值,我们要找到离他最近的。
现在我们有n个x,打比方说有n=100,在这里k假设先定义成30000, k也是一个参数可以自己改。
那对应到表格内,如果这个问题是一个回归问题,我们就那最近的点求一个平均值,如果是分类问题,我们就看附近的所有点哪一个分类出现的最多就可以了。
那按照表格内的数据,假如新出现的这个 x i x_i xi附近是x1, x2, x3, x4,回归问题就是(0.38+1.27+3.56+3.19)/4, 分类问题就是(0, 1, 0)。
这个就是KNN的原理,如果要手动去写的话,按照大家水平不到5分钟就能把这个分类和回归的全部写完。
它实现起来真的特别简单,而且解释起来也很好解释。比方说它预测出来是红色,为什么是红色呢?因为离我最近的3个或者5个占大多数的是红色。
它也有一些缺点,比较大的缺点是什么呢?
一个显著的缺点就是当我们要求的这个点附近完全没有值,离他最近的那个值都离的特别远,那这个时候我们要去求解,它的值就会跑到很远但是离它最近的那些点之间。
KNN找的是和自己最类似的,但是如果他找不到和自己最类似的,他就傻了。
总结一下KNN的优缺点:
| 优点 | 缺点 |
|---|---|
| 容易实现、容易理解 | 运行时间长 |
| 模型调整容易,可以方便的改变k的数量,或者给不同距离的k进行加权 | 容易被异常值影响 |
| 适合解决各种复杂问题(分类、回归、高纬、低纬、复杂关系、简单关系) | 所需空间大 |
| 高纬空间的距离区分度不大 |
关于这个时间久,我们来看一个问题:KNN的时间复杂度是多少?
如果是2.7Ghz英特尔i7处理器,训练数据有1千万哥数据是300维,定义的k=11, 则预测100个实例需要多久?
几毫秒、几秒、几分钟、几个小时还是几天?
2.7Ghz,Ghz就是一秒钟可以运行一个G, 一个G就是2的11次方。
那么估算下来其实应该是几个小时的操作。
那在一些大厂,阿里,蚂蚁,微信等等,那随随便便都是几千万的数据。
所以KNN更合适数据量小的情况。
还有就是我们说一个数学上的概念,当一个向量的维度很高的时候,比如说几百几千维,那个时候的向量就会有一个特点,基本上任意两个向量之间的距离都差不多,区别不是很大。
所以对于KNN这种在高纬向量里面做检索,整个距离差的也不大。
我们需要了解一点,机器学习里面分了两种方式,第一种叫lazy-learning,第二种叫eager learning。
lazy-learning就是懒惰的学习,KNN就是这种方式。KNN是典型的一种lazy-learning。
KNN只是简单的内容记下来,然后去找了一个最接近的东西。lazy-learning最大的问题就是所观测到的是它周围的这些结果。
Data site是比较少的维度,其实效果倒也可以。
为什么要用Lazy呢,这个其实和东西方的教育观念的一个差别,在我们传统观念中的那种勤奋,就是死记硬背的埋头苦读其实就是一种Lazy,其含义是思维上比较Lazy。
然后比较擅长总结归纳,然后分析预测这种我们叫做的eager。
这种方法看到的更加全面,要看到更加广阔的问题,然后抽象出更高层次的函数。我们把这种叫做eager learning。
基本上在咱们整个课程里面除了KNN算法,别的全部都是eager。
贝叶斯
接着我们来讲一下贝叶斯,首先我们来看一段文本:
对于某种商品,根据以往购买的数据,在任意投放广告,未进行特点渠道优化的时候,点击广告到购买商品的比率为7%,自然形成的用户中,本科及以上学历的用户占15%,本科以下学历占85%;现在有一笔广告预算,本科及以上学历渠道的获客成本市场100元每人,本科以下人群投放广告的成本是70元每人。问,该广告投放到本科及以上学历专门的人群还是本科以下人群?(本科及以上学历占总国人的比例约为5%,2016年国家统计局数据)
假如遇到这种问题的时候, 一般都会有两拨人互相PK,互相撕扯。一波人认为顾客里面买东西的有15%的是本科生,本科生比例还挺高,应该大力发展本科生这部分用户,应该把广告主要往本科生这边投。另外一波人会说,有85%的人是本科以下学历的人,而且国家有95%的人是本科以下学历,所以这个市场更大,应该去投本科以下的学历。
这是非常实际的一个问题,假如你以后在公司里的遇到这个问题的时候怎么样去估计呢?我们可以做一个比较简单的数学式子,其实现在我们要估算两个概率,第一个概率是本科及以上的人看见了广告买东西的概率是多少,另外一个就是本科以下的人看见广告买东西的概率是多少。
但是我们现在没有这个数据,只有购买的人里边有多少个人是本科以上, 有多少是本科以下。
也就是说,我们现在不知道一个本科生看见广告之后有多少概率会买,但是可以通过一个方法来解决。就是本科及以上的人购买的概率,其实等于如下这个方程:P(A|B) = P(AB) / P(B) = P(B|A)P(A) / P(B)。
对应我们现在面对的这个案例,那其实就等于是:
Pr(购买|本科及以上) = Pr(本科及以上|购买) * Pr(购买) / Pr(本科及以上) = 15% * 7% / 5% = 21%
Pr(购买|本科以下) = Pr(本科以下|购买) * Pr(购买) / Pr(本科以下) = 85% * 7% / 95% = 6.26%
贝叶斯其实也就是就是这个方法。
我们根据得出的结论,本科及以上每个人的广告成本为100块钱,有21%的人会买,所以平均成交一个人需要花476,100/21 = 476。
同理本科以下的人每个广告成本是70%, 但是最终会购买东西的概率只有6%, 所以说最终成本是1,180块。70 / 6% = 1167。
那假如咱们的产品卖2,000,花100万广告费只投放给本科以上的人群,那公司就可以收入420万,投给本科以下的人,就只能卖116.7万。
这个例子是一个非常典型的商业决策例子,这种决策都有个特点,未来的事情谁都说不上。过去的事情板上钉钉的已经发生了。
我们再说一个很典型的例子,一个骰子连续丢出4次6, 那第5次出现6的概率到底是大于1/6还是小于1/6,还是等于1/6?
等于1/6的说法,因为骰子出不出1/6每一次事件之间是独立的,所以说第五次也是1/6。小于1/6的说法,已经出了那么多6了,接下来不应该出6了。而对于有些人来说,这色子现在明显就是有问题,一个骰子一般来说很少会出现这样的情况,所以这个骰子容易出6,概率肯定是比1/6大。
所以一般来说,比较聪明的决策是把未来看成是过去的再次发生。贝叶斯分类其实就是做这件事情的。
贝叶斯定理表示了在给定先验概率和条件概率的情况下,如何计算后验概率。
P ( A ∣ B ) = P ( B ∣ A ) ∗ P ( A ) P ( B ) \begin{align*} P(A|B) = \frac{P(B|A)*P(A)}{P(B)} \end{align*} P(A∣B)=P(B)P(B∣A)∗P(A)
- P(A|B)是后验概率,表示在给定观测数据B后事件A发生的概率。
- P(B|A)是条件概率,表示事件A发生的情况下事件B发生的概率。
- P(A)是先验概率,表示事件A在没有观测数据B的情况下的概率。
- P(B)是边际概率,表示事件B发生的总概率。
在朴素贝叶斯分类中,我们使用特征向量X=(x1,x2,…,xn)来表示一个样本,其中x_i是第i个特征的取值。我们希望根据这些特征来分类样本为不同的类别C。
p ( C k , x 1 , . . . , x n ) = p ( x 1 , . . . , x n , C k ) = p ( x 1 ∣ x 2 , . . . , x n , C k ) p ( x 2 , . . . , x n , C k ) = p ( x 1 ∣ x 2 , . . . , x n , C k ) p ( x 2 ∣ x 3 , . . . , x n , C k ) p ( x 3 , . . . , x n , C k ) = . . . = p ( x 1 ∣ x 2 , . . . , x n , C k ) p ( x 2 ∣ x 3 , . . . , x n , C k ) . . . p ( x n − 1 ∣ x n , C k ) p ( x n ∣ C k ) p ( C k ) \begin{align*} p(C_k,x_1,...,x_n) & = p(x_1,...,x_n, C_k) \\ & = p(x_1|x_2,...,x_n,C_k)p(x_2,...,x_n,C_k) \\ & = p(x_1|x_2,...,x_n,C_k)p(x_2|x_3,...,x_n,C_k)p(x_3,...,x_n,C_k) \\ & = ... \\ & = p(x_1|x_2,...,x_n,C_k)p(x_2|x_3,...,x_n,C_k)...p(x_{n-1}|x_n,C_k)p(x_n|C_k)p(C_k) \end{align*} p(Ck,x1,...,xn)=p(x1,...,xn,Ck)=p(x1∣x2,...,xn,Ck)p(x2,...,xn,Ck)=p(x1∣x2,...,xn,Ck)p(x2∣x3,...,xn,Ck)p(x3,...,xn,Ck)=...=p(x1∣x2,...,xn,Ck)p(x2∣x3,...,xn,Ck)...p(xn−1∣xn,Ck)p(xn∣Ck)p(Ck)
我们要做这个决策,在以上的式子基础上做了一个很重要的假设,假设什所有特征之间的条件是独立的,即给定类别C下,特征之间的关系是独立的。这个假设使得计算变得简单,但通常并不成立,尤其实在自然语言处理任务中。
因为这个原因,所以它被称为Naive Bayes,就是我们通常所称的「朴素贝叶斯」。其实Naive真正的翻译应该是「幼稚的」。
简化后,朴素贝叶斯分类器的数学公式:
- P(C|X)是后验概率,表示在给定特征向量 X 的情况下,样本属于类别 C 的概率。
- P(X|C): 是似然度,表示在类别 C 下观测到特征向量 X 的概率。基于朴素独立性假设,可以将它分解为各个特征的条件概率的乘积: P ( X ∣ C ) = P ( x 1 ∣ C ) ∗ P ( x 2 ∣ C ) ∗ . . . ∗ P ( x n ∣ C ) P(X|C) = P(x_1|C)*P(x_2|C)*...*P(x_n|C) P(X∣C)=P(x1∣C)∗P(x2∣C)∗...∗P(xn∣C)
- P© 是先验概率,表示样本属于类别 C 的概率。
- P(X)是归一化常数,用于确保后验概率的总和为1。
为了进行分类决策,朴素贝叶斯分类器计算每个类别的后验概率,然后选择具有最高后验概率的类别作为分类结果。数学上,这可以表示为:
C M A P = arg m a x c P ( C ∣ X ) \begin{align*} C_{MAP} = \arg max_cP(C|X) \end{align*} CMAP=argmaxcP(C∣X)
其中 C M A P C_{MAP} CMAP是最可能的类别。
比方下面这个列表:
| Example No. | Color | Type | Origin | Stolen? |
|---|---|---|---|---|
| 1 | Red | Sports | Domestic | YES |
| 2 | Red | Sports | Domestic | NO |
| 3 | Red | Sports | Domestic | YES |
| 4 | Yellow | Sports | Domestic | NO |
| 5 | Yellow | Sports | Imported | YES |
| 6 | Yellow | SUV | Imported | NO |
| 7 | Yellow | SUV | Imported | YES |
| 8 | Yellow | SUV | Domestic | NO |
| 9 | Red | SUV | Imported | NO |
| 10 | Red | Sports | Imported | YES |
列表中分别有Color,车的颜色,Type,车的型号,Origin,车的产地,以及Stolen,是否被偷。
我们令 x 1 x_1 x1 = color, x 2 x_2 x2 = type, x 3 x_3 x3 = origin,那么 x 1 , x 2 , x 3 x_1,x_2,x_3 x1,x2,x3现在就是特征。
假如基于上面朴素贝叶斯的数学公式,我们得到:
P ( C 1 ∣ x ) = 分子 P ( x ) P ( C 2 ∣ x ) = 分子 P ( x ) \begin{align*} P(C_1 |x) = \frac{分子}{P(x)} \\ P(C_2 |x) = \frac{分子}{P(x)} \\ \end{align*} P(C1∣x)=P(x)分子P(C2∣x)=P(x)分子
我们可以发觉,它们的分母其实都是一样的,都是 P ( x ) P(x) P(x)。虽然我们并不知道 P ( x ) P(x) P(x)是多少,但是我们要比较的是 P ( C 1 ∣ x ) P(C_1|x) P(C1∣x)和 P ( C 2 ∣ x ) P(C_2|x) P(C2∣x)的大小,所以我们完全可以不考虑一样大小的分母,就只比较分子大小就可以了。
那我们就将式子变为:
P ( C 1 ∣ x ) = P ( x 1 ∣ C 1 ) P ( x 2 ∣ C 1 ) P ( x 3 ∣ C 1 ) P ( C 1 ) P ( C 2 ∣ x ) = P ( x 1 ∣ C 2 ) P ( x 2 ∣ C 2 ) P ( x 3 ∣ C 2 ) P ( C 2 ) \begin{align*} P(C_1|x) = P(x_1|C_1)P(x_2|C_1)P(x_3|C_1)P(C_1) \\ P(C_2|x) = P(x_1|C_2)P(x_2|C_2)P(x_3|C_2)P(C_2) \end{align*} P(C1∣x)=P(x1∣C1)P(x2∣C1)P(x3∣C1)P(C1)P(C2∣x)=P(x1∣C2)P(x2∣C2)P(x3∣C2)P(C2)
我们拿一个来分析,其中的 P ( x 1 ∣ C 1 ) P(x_1|C_1) P(x1∣C1), 假设现在 x 1 = R e d , C 1 = S t o l e n ( Y E S ) x_1 = Red, C_1 = Stolen(YES) x1=Red,C1=Stolen(YES), 那其实就是 P ( R e d ∣ S t o l e n ( Y E S ) ) P(Red|Stolen(YES)) P(Red∣Stolen(YES)), 也就是所有被偷的里面,Red占多少。那么现在就简单的数数就行了。同理,各个特征的值我们都可以直接数数就能数出来。
P ( C 1 ) P(C_1) P(C1)和 P ( C 2 ) P(C_2) P(C2)的概率是多少? P ( C 1 ) P(C_1) P(C1)和 P ( C 2 ) P(C_2) P(C2)是我们所有的汽车里面, 被偷的占比多少,没偷的占比多少,也是数数就可以数出来。
贝叶斯方法就是我们只需要有一张表格,然后通过数数,通过简单的计算就能够把概率给求出来。黄色的车被偷的概率大还是红色车被偷的概率大,直接就可以数出来。
我们现在看到的贝叶斯都是一个一个类别,但是有的时候,假如说我们所面对的不是0,1这种类别,而是:3, 2, 2.5, 1.6 这种实数该怎么办呢?我们就要用到「高斯贝叶斯分布」。
高斯贝叶斯分布是在处理连续值的时候一个非常典型的做法,就是把连续值做一个分布,做一个离散化处理:
p ( x = v ∣ C k ) = 1 2 π σ k 2 e − ( v − μ k ) 2 2 σ k 2 \begin{align*} p(x = v|C_k) = \frac{1}{\sqrt{2\pi\sigma^2_k}}e^{-\frac{(v-\mu k)^2}{2\sigma^2_k}} \end{align*} p(x=v∣Ck)=2πσk21e−2σk2(v−μk)2
我们只需要知道这一点就行了,贝叶斯解决连续值的问题用了高斯分布。
那么贝叶斯公式的优点是什么呢? 首先它非常容易被实现,基本上写代码都能写到,就是不断的数数。
而且它的预测其实很快,它其实做出了一个概率函数,不像KNN那样还要把所有的数据都存下来,就是存下来了一个判别的数字,直接一乘就可以,特别快。而且在数据量很大的时候效果也比较好。
但是它也有缺点,因为做了一个if的假设,就是X1和X2、X3之间都没有关系,但是其实很多时候x之间是有关系的,这其实是很错误的。
所以当问题变得复杂的时候,贝叶斯往往就不行了。比方说要解决复杂的自然语言处理问题、图像识别问题就不行了。
贝叶斯案例 - 预测广告
咱们来看一个贝叶斯的题目。
假设我们现在有三段短信内容:第一段是一段广告:“快来抢购,这是最大的优惠”;第二段也是一段广告:“今天抢购最优惠”;第三段不是广告,就是一个正常的短信内容:“今天什么时候回家”
- Ad: 快来抢购,这是最大的优惠
- Ad: 今天抢购最优惠
- Text: 今天什么时候回家
现在我们有一个问题:“今天回家抢购”,我们现在要做的是一个垃圾短信拦截,那么这一段内容是属于广告还是不属于广告?
那这个问题,我们实际上就可以用贝叶斯来进行解决。
我们假设 S = 今天回家抢购
那么我们要做的事情就是比较这两个概率的大小:Pr(Ad|S) ~ Pr(Text|S)。
根据贝叶斯的公式,我们就可以得到下面这一步:
Pr(Ad | S) = Pr(Ad | w1 w2 w3)
Pr(Text | S) = Pr(Ad | w1 w2 w3)
然后我们可以将其转化为:
P r ( A d ∣ w 1 w 2 w 3 ) = P r ( w 1 ∣ A d ) P r ( w 2 ∣ A d ) P r ( w 3 ∣ A d ) P r ( A d ) P r ( w 1 w 2 w 3 ) \begin{align*} Pr(Ad|w_1 w_2 w_3) = \frac{Pr(w_1|Ad)Pr(w_2|Ad)Pr(w_3|Ad)Pr(Ad)}{Pr(w_1w_2w_3)} \end{align*} Pr(Ad∣w1w2w3)=Pr(w1w2w3)Pr(w1∣Ad)Pr(w2∣Ad)Pr(w3∣Ad)Pr(Ad)
同理呢,Text和Ad一样可以进行转化:
P r ( T e x t ∣ w 1 w 2 w 3 ) = P r ( w 1 ∣ T e x t ) P r ( w 2 ∣ T e x t ) P r ( w 3 ∣ T e x t ) P r ( T e x t ) P r ( w 1 w 2 w 3 ) \begin{align*} Pr(Text|w_1 w_2 w_3) = \frac{Pr(w_1|Text)Pr(w_2|Text)Pr(w_3|Text)Pr(Text)}{Pr(w_1w_2w_3)} \end{align*} Pr(Text∣w1w2w3)=Pr(w1w2w3)Pr(w1∣Text)Pr(w2∣Text)Pr(w3∣Text)Pr(Text)
其中这些w1, w2, w3就是相关的特征,我们将S分词成w1 = 今天, w2 = 回家, w3 = 抢购。
现在我们来看一下, Pr(Ad)等于多少?等于2/3,也就是我们这三句话中,已知的广告概率是多少。相对的,Pr(Text)就是1/3。
接着我们可以知道。Pr(w1|Ad)就是“今天”在所有广告里出现了几次,
广告一共是2次,“今天”出现了1次,所以应该是1/2。
那Pr(w2|Ad)呢,“回家"没有出现过,不过这里我们要注意,虽然它没有出现过,但是我们不能让它的概率为0,我们要给它一个估计值,这个叫做OOV,out of vocabulary。因为直接为0的话,这个词有比较奇怪就没法去做了,判断不了。
经过简单的分词,我们一共有13个单词,13个单词里边w2出现了一次,所以咱们可以给他一个估计值1/13。
如果没有这个估计值的话, 可能只要在内容里面随机加一些生僻字,就能够躲过系统的检测。
w3是“抢购”,Pr(w3|Ad)就是1。那么Pr(Ad|S)的分子部分就是Pr(Ad) = 2/3, Pr(w1|Ad) = 1/2, Pr(w2|Ad)=1/13, Pr(w3|Ad) = 1。
那我们上节课说过,分母我们其实不用管,也就是Pr(w1 w2 w3)在过程中其实是不用计算的。
我们同理再来看以下Pr(Text|S)的分子,Pr(Text)=1/3, Pr(w1|Text)=1, Pr(w2|Text)=1, Pr(w3|Text)=2/13。
那我们最后可以得到简单的一个小学式子:
P r ( A d ∣ S ) = 1 / 2 ∗ 1 / 13 ∗ 2 / 3 = 1 / 13 ∗ 1 / 3 P r ( T e x t ∣ S ) = 2 / 13 ∗ 1 / 3 \begin{align*} Pr(Ad|S) & = 1/2 * 1/13 * 2/3 = 1/13 * 1/3 \\ Pr(Text|S) & = 2/13*1/3 \end{align*} Pr(Ad∣S)Pr(Text∣S)=1/2∗1/13∗2/3=1/13∗1/3=2/13∗1/3
明显Pr(Text|S)更大一点,所以“今天回家抢购”这句话更大的概率下不是广告。
这个就是贝叶斯的一个应用案例,也是非常常见的一个面实题。
好,那这节课的内容就到这里了,要记得复习。
原文连接:14. 机器学习 - KNN & 贝叶斯