【C++】数据结构实验——顺序表实现大数相加与相乘

一、上机实验的问题和要求：
问题：大数相加与相乘
要求：采取线性表
二、程序设计的基本思想，原理和算法描述：
（包括程序的结构，数据结构，输入/输出设计，符号名说明等）
首先注意到是对大数进行操作，那么就不能通过int、float等数据类型存储大数，因为可能会发生截断导致大数的数位丢失，解决办法就是使用string类型来存储大数，理论上支持最大std::string::max_size()个字节，远远超过int、float、double等类型支持的最大数字。其实个人感觉使用Pyhton来计算大数相加相乘会优于C++。
其次关于算法的设计，如下：

相加：首先将string类型的985,73转成char型数组，创建两个顺序表，给data[]赋值，接着调用reverse函数将数组转置，方便后续的操作，其次相应位相加赋值到flag[]数组里。注意：这里是没必要再新建一个顺序表来存结果的，因为只需要保证新建的数组or顺序表能够容纳相加后结果就行，一个新顺序表会造成内存的浪费。之后进行进位的操作，如果数组中元素≥10就取模10，后一位元素自增1。这里有个坑就是最高位有可能还会再进位，所以flag数组的长度为str_Maxlength + 1(str_MaxLength指的是两个大数中较长的数的位数).最后把flag数组再转置，回归到正常的顺序。
大数相加还是比较容易的。要注意测试程序要全面，比如测试9999999999+1之类，算法设计有缺陷程序会直接报错。
相乘：大数相乘算法个人感觉还是有点难度的，虽然可以不用顺序表，实现更优的大数相乘算法，但复用大数相加的代码也算是挺省事的。
算法大同小异，只不过是相加的行数变多了，flag数组最后一行的长度也需要特殊的计算，即str_MaxLength + second.length() - 1。这些在代码里会有体现。
在输出结果时，通过迭代器删除原string类型中的x和首位可能出现的0
算法具体实现时还会有一些细节需要注意到。
三、源程序及注释
实验一.cpp

// 实验一.cpp : 此文件包含 "main" 函数。程序执行将在此处开始并结束。
//

#include 
#include 
#include 
#include "Seq.h"
using namespace std;

string Add(string first, string second);//Add函数声明
string Multiplication(string first, string second);//Multiplication函数声明


int main()
{
	string first;
	int a;
	string second;//大数用string存储
	cout << "请输入第一个大数：";
	cin >> first;
	cout << "请输入第二个大数：";
	cin >> second;
	cout << "相加后结果为：" << Add(first, second) << '\n';
	cout << "相乘后结果为：" << Multiplication(first, second) << '\n';
}
void Assignment(string str, char* str_pointer, int length)//函数功能：将传入的str赋值到char型数组里
{
	for (int i = 0; i < length; i++)
	{
		if (i < str.length())
		{
			str_pointer[i] = str[i];
		}
		else
		{
			str_pointer[i] = '0';//将str_first和str_second中较短的那个，用0补齐，方便后续的操作
		}
	}
}
string Add(string first, string second)//函数功能：将传入的两个大数(以string类型保存)相加并以string类型return
{
	int str_MaxLength = (first.length() >= second.length() ? first.length() : second.length());//得到两个string中长度较长的长度

	char* str_first = new char[first.length() + 1];//把string转char型数组
	Assignment(first, str_first, str_MaxLength);
	SeqList<char> Seq_first(first.length(), str_first);//建立顺序表Seq_first

	char* str_second = new char[second.length()];//把string转char型数组
	Assignment(second, str_second, str_MaxLength);
	SeqList<char> Seq_second(second.length(), str_second);//建立顺序表Seq_second

	string result = "xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx";//兴建一个100位的string

	Seq_first.Reverse();//调用Reverse函数，将顺序表转置，方便后续的操作
	Seq_second.Reverse();

	int* flag = new int[str_MaxLength + 1];//因为最高位相加后也可能会再进一位，所以在str_MaxLength的基础上还要再加1
	flag[str_MaxLength] = 0;//flag数组存储相加后的结果

	for (int i = 0; i < str_MaxLength; i++)
	{
		flag[i] = Seq_first.ReturnArrayPointer()[i] + Seq_second.ReturnArrayPointer()[i] - '0' - '0';//对应位相加
	}
	for (int i = 0; i < str_MaxLength; i++)
	{
		if (flag[i] >= 10)//如果相加结果≥10，取模10，后一位自增1
		{
			flag[i] %= 10;
			flag[i + 1]++;
		}
	}
	for (int i = 0; i < str_MaxLength + 1; i++)
	{
		result[i] = flag[i] + '0';//flag数组转string
	}

	string::iterator it;//指向string类的迭代器
	for (it = result.begin(); it != result.end(); it++)
	{
		if (*it == 'x')
		{
			result.erase(it); //STL erase函数 消去x
			it--;
		}
	}
	reverse(result.begin(), result.end());//再转置一遍，回到正常的顺序

	it = result.begin();//由于转置后第一位可能出现0，例如0156131，所以要判断消去首位0
	if (*it == '0')
	{
		result.erase(it); //消去首位0
	}

	return result;
}

string Multiplication(string first, string second)
{
	int str_MaxLength = (first.length() >= second.length() ? first.length() : second.length());//得到两个string中长度较长的长度

	char* str_first = new char[first.length() + 1];//把string转char型数组
	Assignment(first, str_first, str_MaxLength);
	SeqList<char> Seq_first(first.length(), str_first);//建立顺序表Seq_first

	char* str_second = new char[second.length()];//把string转char型数组
	Assignment(second, str_second, str_MaxLength);
	SeqList<char> Seq_second(second.length(), str_second);//建立顺序表Seq_second

	string result = "xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx";//兴建一个100位的string

	Seq_first.Reverse();//调用Reverse函数，将顺序表转置，方便后续的操作
	Seq_second.Reverse();

	int** flag = new int* [str_MaxLength + 1];//动态建立二维int数组，大小为str_MaxLength*str_MaxLength + second.length() - 1  +  1*str_MaxLength + second.length() ,注意到最后一行多一个元素，用来存原最高位的进位
	for (int i = 0; i < str_MaxLength + 1; i++) {
		if (i == str_MaxLength)
		{
			flag[i] = new int[str_MaxLength + second.length()];
			flag[i][str_MaxLength + second.length() - 1] = 0;
		}
		else
		{
			flag[i] = new int[str_MaxLength + second.length() - 1];
		}
		for (int j = 0; j < str_MaxLength + second.length() - 1; j++)//令所有的元素为0
		{
			flag[i][j] = 0;
		}
	}


	for (int i = 0, k = 0; i < str_MaxLength; i++, k++)//相乘存放到flag数组里
	{
		for (int j = 0; j < str_MaxLength; j++)
		{
			flag[i][j + k] = (Seq_first.ReturnArrayPointer()[j] - '0') * (Seq_second.ReturnArrayPointer()[i] - '0');
		}
	}
	for (int i = 0; i < str_MaxLength + second.length() - 1; i++)//将相乘结果再按列相加
	{
		for (int j = 0; j < second.length(); j++)
		{
			flag[str_MaxLength][i] += flag[j][i];

		}
	}
	for (int i = 0; i < str_MaxLength + second.length() - 1; i++)//超十进位
	{
		if (flag[str_MaxLength][i] >= 10)
		{
			int temp = flag[str_MaxLength][i] / 10;
			flag[str_MaxLength][i] %= 10;
			flag[str_MaxLength][i + 1] += temp;
		}
	}
	for (int i = 0; i < str_MaxLength + second.length(); i++)
	{
		result[i] = flag[str_MaxLength][i] + '0';//flag数组转string
	}

	string::iterator it;//指向string类的迭代器
	for (it = result.begin(); it != result.end(); it++)
	{
		if (*it == 'x')
		{
			result.erase(it); //STL erase函数 消去x
			it--;
		}
		/*if (*it == '0' && *(it + 1) == '0' && it + 1 != result.end())
		{
			result.erase(it);
			it--;
		}*/
	}
	reverse(result.begin(), result.end());//再转置一遍，回到正常的顺序

	it = result.begin();//由于转置后第一位可能出现0，例如0156131，所以要判断消去首位0
	if (*it == '0')
	{
		result.erase(it); //消去首位0
	}

	return result;
}
// 运行程序: Ctrl + F5 或调试 >“开始执行(不调试)”菜单
// 调试程序: F5 或调试 >“开始调试”菜单

// 入门使用技巧: 
//   1. 使用解决方案资源管理器窗口添加/管理文件
//   2. 使用团队资源管理器窗口连接到源代码管理
//   3. 使用输出窗口查看生成输出和其他消息
//   4. 使用错误列表窗口查看错误
//   5. 转到“项目”>“添加新项”以创建新的代码文件，或转到“项目”>“添加现有项”以将现有代码文件添加到项目
//   6. 将来，若要再次打开此项目，请转到“文件”>“打开”>“项目”并选择 .sln 文件

Seq.h

#pragma once

#include 
using namespace std;

const int MaxSize = 100;
template <typename ElemType>
class SeqList
{
public:
	SeqList();//不含参的构造函数
	SeqList(int length, ElemType str[]);//根据length和str[]生成一个合适的顺序表
	void Reverse();
	ElemType* ReturnArrayPointer()
	{
		return data;
	}
	~SeqList();

private:
	ElemType data[MaxSize];
	int length;
};
template <typename ElemType>
SeqList<ElemType>::SeqList()
{

}
template <typename ElemType>
SeqList<ElemType>::SeqList(int str_length, ElemType str[])//函数功能：创建一个顺序表
{
	if (str_length > MaxSize)
	{
		throw "错误1";
	}
	for (int i = 0; i < MaxSize; i++)
	{
		data[i] = str[i];
		//cout << data[i];
	}
	length = str_length;
}
template <typename ElemType>
void SeqList<ElemType>::Reverse()
{
	for (int i = 0; i <= length / 2; i++)
	{
		ElemType temp = data[i];
		data[i] = data[length - i - 1];
		data[length - i - 1] = temp;
		//cout << "data[i]" << data[i];
	}
}

template <typename ElemType>
SeqList<ElemType>::~SeqList()
{
}

四、运行输出结果：

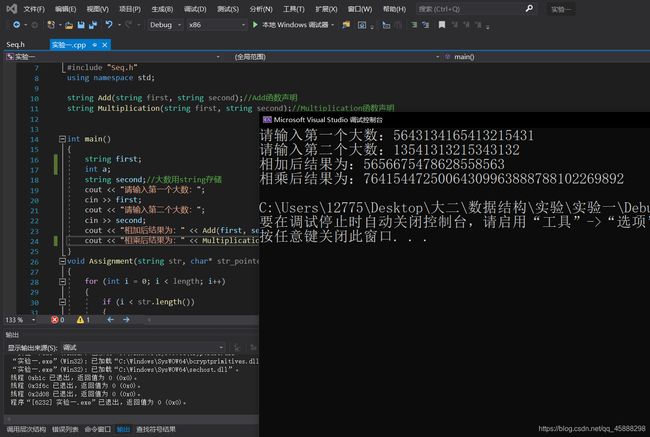
验证：


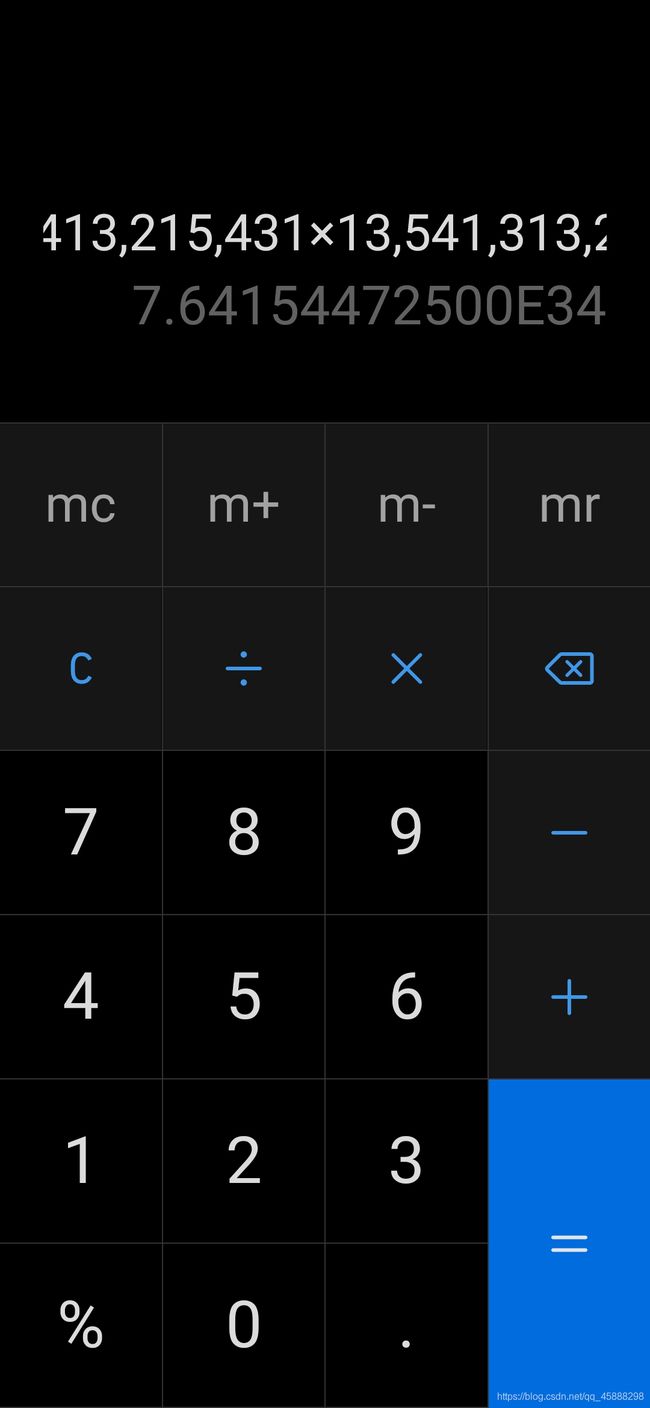
五、调试和运行程序过程中产生的问题及采取的措施：
实验过程中的一些问题及解决办法：
1.程序构建后报LNK2019 不可解析的外部符号的错误
这个问题是同学出现的。查了查资料，一般来讲出现以下情况时，会出现LNK2019的错误：
（1）未链接的对象文件或包含符号定义的库
（2）符号声明的拼写不与符号的定义相同
（3）使用了函数，但类型或参数数目不匹配函数定义
（4）声明但未定义的函数或变量
（5) 调用约定是函数声明和函数定义之间的差异
（6）符号定义在c文件中，但未使用extern C在c++文件中声明
（7）符号定义为静态，并随后被外部文件引用
（8）未定义类的静态成员
（9) 生成依赖项仅定义为解决方案中项目依赖项
（10）第三方库问题和Vcpkg
同学的程序报错原因是4，声明了构造函数与析构函数，但没有实现。另外还有一种情况没有在上面列出，就是在vs中使用类模板时，必须将函数的声明和实现放在同一个.h文件中。室友将函数的实现放在了其他的.cpp文件里，而将函数的声明放在了.h文件里，人为分离。在使用类模板时，vs是不允许这么操作的，即便在编辑时vs不会报错。
2.编译后出现未加载wntdll.pdb的错误
查了一些资料，众说纷纭，后来发现是自己本身的代码有问题，出现了指针越界访问，以及数组越界的情况。事实上，未加载wntdll.pdb这个错误绝大部分是代码的问题，而不是vs编译的问题。
为了避免此类问题，解决办法就是提前设计好算法，严格按照算法实现程序。不设计算法，直接上机实现，后期心态会崩溃…
3.新建一个顺序表C的必要性
前面已经提到，为了存储A+B的结果，是不需要再新建一个顺序表C的，会造成大量空间的浪费。只需要存放结果的数组or顺序表长度满足要求即可。
4.使用线性表解决大数问题的合理性
本次程序并没有用到太多顺序表的功能，只用到了顺序表的建立、初始化，至于删除、插入则是完全没用到。因此个人感觉完全可以使用纯数组来代替线性表。
六、对算法的程序的讨论、分析，改进设想，其它经验教训：
1.善用C++的特性
C++比C的一大优势就是提供了大量的API，比如代码用到的求字符串长度的API：first.length(),转置字符串的API：reverse(),删除字符串特定元素的API：erase()等。这些API已经被封装，直接调用，非常方便。
2.算法设计
一定要提前设计好算法，这次实验我是直接上机敲了，想到哪就敲到哪，导致的结果就是debug非常崩溃，又没有全删重写的勇气，因此以后的程序务必先设计好算法。
3.程序中的大数相加相乘算法
关于大数相加，教材上是新建了一个线性表C来存储A+B的值，这其实是没有必要的，会造成内存的浪费。因为只需要使C能够容纳A+B后值就可以了，无需使C和A、B等长，这里可以使用动态内存分配。
关于大数相乘，程序使用的是模拟乘法累加 - 改进算法，时间复杂度O(n^2)，
其实还有更高效的算法：Karatsuba算法，时间复杂度为O(n^log23)，
如果n很大，可以采用快速傅里叶变化FFT，把时间复杂度降到O(n^1.149)，非常的高效。
但这次实验是以线性表为基础，所以我也没有去实现，只是看了一些博客。
4.flag数组内存浪费问题
在算法设计图片里可以看到大数相乘算法的flag数组中存在0，这是因为second数组里每个数字和first数组每个元素一次相乘后的结果相加时要错位(相邻错1位)，错位填0，事实上是没有必要的。
一开始我是不这么实现的，想通过代码直接实现逻辑上的错位，内存上不错位，但想了很长时间都没有实现，只能放弃这个想法，实现内存上错位，逻辑上错位，得到正确的结果。从目前情况来看，当位数很大出现很多错位时，相应的会出现很多0位，会造成一定的内存浪费。
不过到现在，自己还是没能想出内存不错位的代码来。
5.总结
总的来说，这次的实验锻炼了自己的算法设计能力与自己的心态，加深了对顺序表的熟悉程度。

程序未经过全面的测试，可能存在未知的bug。

以上 如果此篇博客对您有帮助欢迎点赞与转发 有疑问请留言或私信 2020/9/19