算法通关村第一关链表青铜挑战笔记
单链表概念
任何数据结构的基础都是创建+增删改查,由这几个操作可以构造很多算法题
什么是链表
首先看一下什么是链表?使用链表存储数据,不强制要求数据在内存中集中存储,各个元素可以分散存储在内存中。例如,使用链表存储 4,,15,,7,,40),各个元素在内存中的存储状态可能是: 如下图:
显然,我们只需要记住元素 4 的存储位置,通过它的指针就可以找到元素 15,通过元素 15 的指针就可以找到元素 7,以此类推,各个元素的先后次序一目了然。
可以看到,数据不仅没有集中存放,在内存中的存储次序也是混乱的。那么,链表是如何存储数据间逻辑关系的呢? 链表存储数据间逻辑关系的实现方案是: 为每一个元素配置一个指针,每人元素的指针都指向自己的直接后继元素,也就是上图图所示的样子。
像上图这样,数据元素随机存储在内存中,通过指针维系数据之间“一对一”的逻辑关系,这样的存储结构就是链表。
下面是否链表概念:
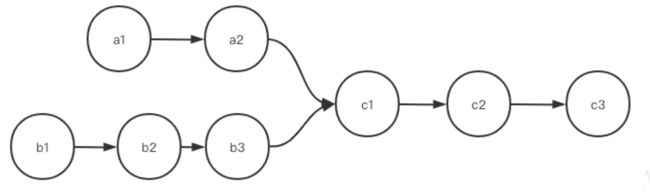
上面第一个图是满足单链表要求的,因为我们说链表要求环环相扣,核心是一个结点只能有一个后继,但不代表个结点只能有一个被指向。第一个图中,c1被a2和b3同时指向,这是没关系的。这就好比法律倡导一夫一妻,你只能爱一个人,但是可以都多个人爱你。
第二图就不满足要求了,因为c1有两个后继a5和b4
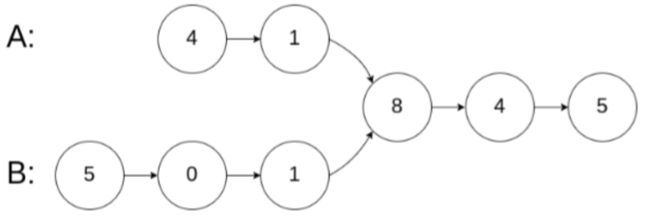
另外在做题的时候要注意比较的是值还是结点,有时可能两个结点的值相等,但并不是同一个结点,例如下图中有两个结点的值都是1,但并不是同一个结点。
链表相关概念
节点和头结点:
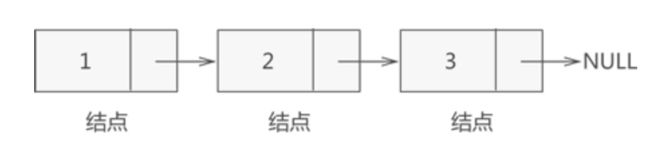
在链表中,每个点都由值和指向下一个结点的地址组成的独立的单元,称为一个结点,有时也称为节点,合义都是一样的。
对于单链表,如果知道了第一个元素,就可以通过遍历访问整个链表
因此第一个结点最重要,一般称为头结点
*虚拟节点:
在做题以及在工程里经常会看到虚拟结点的概念,其实就是一个结点dummyNode,其next指针指向head,也就是dummyNode.next=head.
因此,如果我们在算法里使用了虚拟结点,则要注意如果要获得head结点,或者从方法(函数)里返回的时候,则应使用dummyNode.next。
另外注意,dummyNode的val不会被使用,初始化为0或者-1等都是可以的。既然值不会使用,那虚拟结点有啥用呢?简单来说,就是为了方便我们处理首部结点,否则我们需要在代码里单独处理首部结点的问题。在链表反转里,我们会看到该方式可以大大降低解题难度。
如何构造链表
在链表中,每个结点数据元素都配有一个指针,这意味着,链表上的每人“元素”都长下图这个样子:
数据域用来存储元素的值,指针域用来存放指针。数据结构中,通常将上图这样的整体称为结点。
也就是说,链表中实际存放的是一个一个的结点,数据元素存放在各个结点的数据域中。举个简单的例子,下图中{1,2,3) 的存储状态用链表表示,如下图所示:
Java代码定义:
public class Node {
public int data;
public Node next;
//构造方法,创建新节点时,把data存入当前结点数据域中
public Node(int data) {
this.data = data;
}
}如果我们要创建一个值为 1 2 3 4 5 的链表,可以这么做:
public class LinkedList {
public static void main(String[] args) {
// 创建头节点
Node head = new Node(1);
Node current = head;
// 添加剩余的节点
for (int i = 2; i <= 5; i++) {
Node newNode = new Node(i);
current.next = newNode;
current = newNode;
}
// 输出链表的值
current = head;
while (current != null) {
System.out.print(current.data + " ");
current = current.next;
}
}
}输出结果:
1 2 3 4 5链表的增删改查
遍历链表
对于单链表,不管进行什么操作,一定是从头开始逐个向后访问,所以操作之后是否还能找到表头非常重要。一定要注意”狗熊掰棒子"问题,也就是只顾当前位置而将标记表头的指针丢掉了。
代码示例:
public static void getListData(Node head) {
Node current = head;
while (current != null) {
System.out.println(current.data);
current = current.next;
}
}链表插入
单链表的插入操作要考虑二种情况: 首部、中部和尾部。
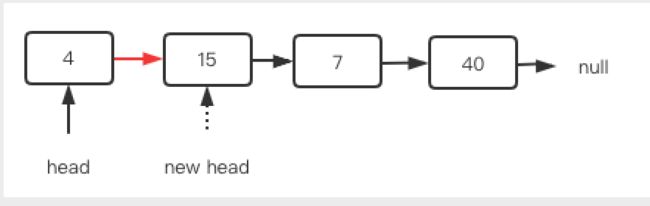
(1)在链表的表头插入
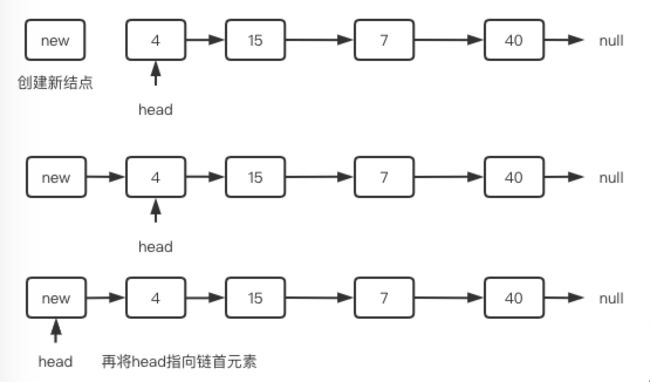
链表表头插入新结点非常简单,容易出错的是经常会忘了head需要重新指向表头。 我们创建一个新结点newNode,怎么连接到原来的链表上呢? 执行newNode->next=head即可。之后我们要遍历新链表就要从newNode开始一路next向下了是吧,但是我们还是习惯让head来表示,所以让head=newNode就行了,如下图:
步骤简述:
- 创建一个新的节点,并为其分配内存空间。
- 将新节点的指针域(存储下一个节点的地址)指向当前的头节点。
- 将头指针(head)指向新节点的地址,以使得新节点成为新的头节点
(2)在链表中间插入
在中间位置插入,我们必须先遍历找到要插入的位置,然后将当前位置接入到前驱结点和后继结点之间,但是到了该位置之后我们却不能获得前驱结点了,也就无法将结点接入进来了。这就好比一边过河一边拆桥,结果自己也回不去了。
为此,我们要在目标结点的前一个位置停下来,
也就是使用cur->next的值而不是cur的值来判断,这是链表最常用的策略。
例如下图中,如果要在7的前面插入,当cur->next=node(7)了就应该停下来,
此时cur->val=15。然后需要给newNode前后接两根线,
此时只能先让new->next=node(15)->next(图中虚线),
然后node(15)->next=new,而目顺序还不能错.
想一下为什么不能颠倒顺序?
由于每个节点都只有一个next,因此执行了node(15)->next=new之后,结点15和7之间的连线就自动断开了,如下图所示:
步骤简述:
- 创建一个新节点,并为其分配内存空间。
- 遍历链表,找到要插入位置的前一个节点。
- 将新节点的指针域指向前一个节点原本指向的下一个节点。
- 将前一个节点的指针域指向新节点。
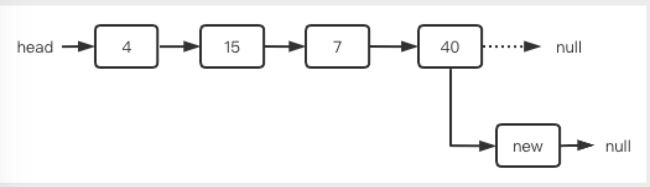
(3)在单链表的结尾插入
表尾插入就比较容易了,我们只要将尾结点指向新结点就行了。
步骤简述:
- 创建一个新节点,并为其分配内存空间。
- 将新节点的数据赋值为要添加的数据。
- 将新节点的指针域设置为null,表示它是链表的最后一个节点。
- 将最后一个节点的指针域指向新节点。
综上所述:
//链表插入结点方法
//head 头结点
//nodeInsert 待插入结点
//position 待插入位置,从1开始
//return 返回删除后的链表头结点
public static Node insertNode(Node head, Node nodeInsert, int position){
//插入的结点就是链表的头结点,是第一个
if (head == null){
//待插入结点不用插入了,直接返回头结点
return nodeInsert;
}
//判断插入结点位置是否越界
//假如size是2,position插入可以是1、2、3
//所以是 position > size + 1
int size = getLength(head);
if (position < 1 || position > size + 1){
System.out.println("插入位置参数越界");
//位置越界,还是返回头结点
return head;
}
//表头插入
if (position == 1){
//head头结点转给新插入在表头的nodeInsert
//再返回nodeInsert
nodeInsert.next = head;
return nodeInsert;
}
//链中、链尾插入
//创建一个pNode结点从头结点开始遍历,让pNode指向position位置节点上一个节点
//这里position被上面的size被限制住了,不用考虑pNode=null
Node pNode = head;
int count = 1;
while (count < position - 1){
pNode = pNode.next;
count++;
}
//pNode找到后,开始nodeInsert插入
nodeInsert.next = pNode.next;
pNode.next = nodeInsert;
return head;
}链表删除
删除同样分为在删除头部元素,删除中间元素和删除尾部元素。
(1)删除表头结点
删除表头元素还是比较简单的,一般只要执行head=head->next就行了。
如下图,将head向前移动一次之后,原来的结点不可达,然后就可以将其删掉了。
步骤简述:
- 创建一个指针变量来保存链表的头指针。
- 将头指针指向链表的下一个节点,跳过原来的头节点,使原来的头节点不可达。
(2)删除最后一个结点
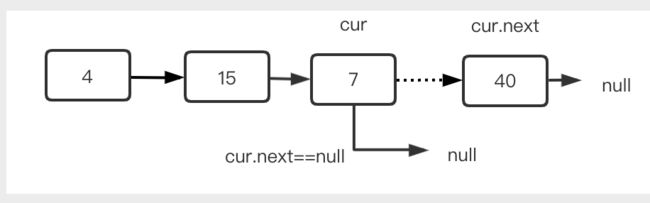
删除的过程不算复杂,也是找到要删除的结点的前驱结点,这里同样要在提前一个位置判断,例如下图中删除40,其前驱结点为7。
遍历的时候需要判断cur->next是否为40,如果是,则只要执行cur>next=null即可,此时结点40就可以放心删掉了。
步骤简述:
- 如果链表为空,无法进行删除操作,直接返回。
- 如果链表只有一个节点,即头节点,将头指针设置为nullptr,释放原来的头节点所占用的内存空间,然后返回。
- 遍历链表,直到找到倒数第二个节点。可以使用两个指针,一个指向当前节点,另一个指向下一个节点。
- 将倒数第二个节点的指针域设置为nullptr,表示它是链表的最后一个节点。
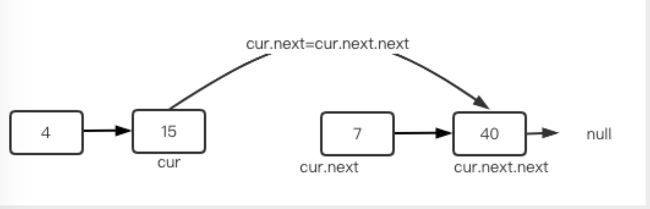
(3)删除中间链表
删除中间结点时,也会要用curnext来比较,找到位置后,将cur->next指针的值更新为cur->next->next,然后就可以放心的将node(6)删掉了,如下图所示:
步骤简述:
- 如果链表为空或只有一个节点,则无法进行删除操作,直接返回。
- 使用两个指针变量,一个指向当前节点,另一个指向当前节点的前一个节点。
- 遍历链表,直到找到目标节点。可以通过比较当前节点的值或者其他条件来确定目标节点。
- 将前一个节点的指针域指向目标节点的下一个节点,跳过目标节点。
代码实现:
//链表删除节点方法
//head 头结点
//position 删除节点位置,取值从1开始
public static Node deleteNode(Node head, int position){
//链表中就只有头结点一个,删完就返回空
if (head == null){
return null;
}
//判断插入结点位置是否越界
int size = getLength(head);
//假如size是2,position删除只能是1、2
//所以是 position > size 要和节点插入的position区分
if (position < 1 || position > size){
System.out.println("输入参数有误");
return head;
}
//链首删除
if (position == 1){
return head.next;
}else{
//链中、链尾删除
//创建一个pNode结点从头结点开始遍历,找到position位置节点上一个节点
Node pNode = head;
int count = 1;
while (count < position - 1){
pNode = pNode.next;
count++;
}
//跳过pNode后面的position结点,实现删除
pNode.next = pNode.next.next;
}
return head;
}回顾思考
1.理解C语言里是如何构造出链表的
链表可以将其看作由一个个称为节点的独立对象组成的。
每个节点包含两部分内容:
一个是数据域:用于存储具体数据的字段
一个是指针域:一个指向下一个节点的指针
这样,我们可以通过节点之间的指针链接,将它们连接成一个链表的形式。
表头:不存储任何数据,仅用于标识链表的起始位置
2.链表增加元素,首部、中间和尾部分别会有什么问题,该如何处理?
(1)在链表首部添加元素
注意点:添加节点后注意表头的指向迁移
- 首先,创建一个新的节点,该节点包含要添加的数据。
- 将新节点的指针域指向原链表的头节点,即将原链表作为新节点的下一个节点。
- 将新节点设置为链表的新头节点,即将链表的头指针指向新节点。
(2)在链表中间添加元素
注意点:注意插入结点前后的指针域迁移
- 创建一个新节点,并为其分配内存空间。
- 遍历链表,找到要插入位置的前一个节点。
- 将新节点的指针域指向前一个节点原本指向的下一个节点。
- 将前一个节点的指针域指向新节点。
(3)在链表尾部添加元素
- 创建一个新节点,并为其分配内存空间。
- 将新节点的指针域设置为null,表示它是链表的最后一个节点。
- 将最后一个节点的指针域指向新节点。
3.链表删除元素,首部、中间和尾部分别会有什么问题,该如何处理?
(1)链表删除首部元素
注意点:新建一个新的表头指向第二个结点即可
- 创建一个指针变量来保存链表的头指针。
- 将头指针指向链表的下一个节点,跳过原来的头节点,使原来的头节点不可达。
- 释放原来的头节点所占用的内存空间。
(2)链表删除中间元素
注意点:指针域的迁移
- 遍历链表,直到找到目标节点。
- 将前一个节点的指针域指向目标节点的下一个节点,跳过目标节点。
- 释放目标节点所占用的内存空间。
(3)链表删除尾部元素
- 遍历链表,直到找到倒数第二个节点。
- 将倒数第二个节点的指针域设置为null,表示它是链表的最后一个节点。
- 释放最后一个节点所占用的内存空间。
4.双向链表是如何构造的,如何实现元素的插入和删除.
单向链表是一种数据结构,它由一系列节点组成,每个节点包含一个数据元素和一个指向下一个节点的指针。每个节点只能访问它后面的节点,不能访问前面的节点。链表的头节点是第一个节点,尾节点是最后一个节点,尾节点的指针指向空
双向链表也是一种数据结构,它与单向链表相似,但每个节点除了包含一个指向下一个节点的指针外,还包含一个指向前一个节点的指针。这样,每个节点既可以访问它后面的节点,也可以访问它前面的节点。双向链表的头节点是第一个节点,尾节点是最后一个节点,头节点的前指针和尾节点的后指针都指向空
注意点:和前面一样,分别要考虑结点要开头、中间、末尾的情况
- 首先判断要删除的节点是否为头节点或尾节点。如果是头节点,将头指针指向下一个节点,并将下一个节点的前驱指针置为null。如果是尾节点,将尾指针指向前一个节点,并将前一个节点的后继指针置为null。
- 如果要删除的节点不是头节点或尾节点,则需要修改前一个节点和后一个节点的指针。将前一个节点的后继指针指向要删除节点的后一个节点,将后一个节点的前驱指针指向要删除节点的前一个节点。
- 最后,将要删除的节点从内存中释放,完成节点的删除操作。
双链表详解
在双链表中,每个节点的结构通常包含三个部分:前驱指针、数据域和后继指针。
- 前驱指针(Prev Pointer):前驱指针指向链表中的前一个节点。对于双链表中的第一个节点,前驱指针通常为空或指向一个特定的值,用来表示前面没有节点了。
- 数据域(Data):数据域存储节点的数据值,可以是任意类型的数据。
- 后继指针(Next Pointer):后继指针指向链表中的下一个节点。对于双链表中的最后一个节点,后继指针通常为空或指向一个特定的值,用来表示后面没有节点了。
通过前驱指针和后继指针,每个节点都可以在链表中的前一个节点和后一个节点之间建立双向连接,实现双向遍历和操作。
双链表结构Java代码:
public class DoubleNode {
// 用 public 修饰是为了图方便
public int data;
public DoubleNode prev;
public DoubleNode next;
// 构造方法,创建新节点时,把 data 存入当前结点数据域中
public DoubleNode(int data) {
this.data = data;
}
}双链表插入代码:
//head 头结点
//nodeInsert 待插入结点
//position 待插入位置,从1开始
//return 返回插入后的链表头结点
public static DoubleNode insertNode(DoubleNode head, DoubleNode nodeInsert, int position) {
// 插入的结点就是链表的头结点,是第一个
if (head == null) {
// 待插入结点不用插入了,直接返回头结点
return nodeInsert;
}
// 判断插入结点位置是否越界
int size = getLength(head);
if (position < 1 || position > size + 1) {
System.out.println("插入位置参数越界");
// 位置越界,还是返回头结点
return head;
}
// 表头插入
if (position == 1) {
// 将新插入的节点作为新的头结点
nodeInsert.next = head;
// 更新头结点的前一个节点为新插入的节点
nodeInsert.prev = null;
// 如果原头结点不为空,则更新原头结点的后一个节点为新插入的节点
if (head != null) {
head.prev = nodeInsert;
}
// 返回新插入的节点作为新的头结点
return nodeInsert;
}
// 链中、链尾插入
DoubleNode pNode = head;
int count = 1;
while (count < position - 1) {
pNode = pNode.next;
count++;
}
// pNode 找到后,开始插入新节点
nodeInsert.next = pNode.next;
nodeInsert.prev = pNode;
if (pNode.next != null) {
pNode.next.prev = nodeInsert;
}
pNode.next = nodeInsert;
return head;
}双链表删除代码:
//head 头结点
//nodeInsert 待删除结点
//return 返回删除后的链表头结点
public static DoubleNode deleteNode(DoubleNode head, int position) {
// 链表中只有一个头结点,删除后返回空
if (head == null) {
return null;
}
// 判断插入节点位置是否越界
int size = getLength(head);
if (position < 1 || position > size) {
System.out.println("输入参数有误");
return head;
}
// 链首删除
if (position == 1) {
return head.next;
} else {
// 链中、链尾删除
DoubleNode pNode = head;
int count = 1;
while (count < position - 1) {
pNode = pNode.next;
count++;
}
// 获取要删除节点的上一个节点
DoubleNode prevNode = pNode;
// 获取要删除节点的下一个节点
DoubleNode nextNode = pNode.next.next;
// 更新上一个节点的next指针,跳过要删除的节点
prevNode.next = nextNode;
// 更新要删除节点的下一个节点的prev指针,跳过要删除的节点
nextNode.prev = prevNode;
}
return head;
}最后推荐一个知识星球
详情可至链接
https://yupi.icu/
https://wx.zsxq.com/mweb/views/joingroup/join_group.html?group_id=51122858222824&secret=218iwimac5qa452q3o6pz2os5ajftbb3&inviter_id=212542158511251&share_from=GroupQRCodeSaved&keyword=11RQPQaqp&abtest_source=ABTest_90