因果推断《Causal Inference in Python》中文笔记第3章 图形因果模型
《Causal Inference in Python: Applying Causal Inference in the Tech Industry》因果推断啃书系列
第1章 因果推断导论
第2章 随机实验与统计学回顾
第3章 图形因果模型
持续更新中:
第4章 线性回归的不合理有效性
第5章 倾向分
第6章 效果异质性
第7章 元学习
第8章 双差分法
第9章 综合控制
第10章 Geo实验与Switchback实验
第11章 不依从性与工具
第12章 后续行动
《Causal Inference in Python》第3章 图形因果模型
- 第3章 图形因果模型
-
- 3.1 关于因果关系
-
- 3.1.1 可视化因果关系
- 3.1.2 顾问价有所值吗?
- 3.2 图形模型速成课程
-
- 3.2.1 链(Chains)
- 3.2.2 分叉(Forks)
- 3.2.3 不道德(Immorality)与碰撞器(Collider)
- 3.2.5 使用Python进行图形查询
- 3.3 重新识别
- 3.5 正值性假设(Positivity Assumption)
- 3.6 一个在数据中进行识别的案例
- 3.7 混杂偏倚(Confounding Bias)
-
- 3.7.1 代理混杂因子(Surrogate Confounding)
- 3.8 选择偏差(Selection Bias)
-
- 3.8.1 给碰撞器设定条件
- 3.8.2 选择偏差的调整
- 3.8.3 给中介设置条件
- 3.9 要点总结
第3章 图形因果模型
在第一章中,你看到了因果推理如何被分解成两个问题:识别和估算。在本章中,你将深入了解识别部分,这可以说是最具挑战性的部分。本章主要是理论性的,你将使用图形模型,而不必使用数据估计其参数。识别是因果推理的核心,因此学习其理论是解决现实生活中因果问题的基础。在本章中,你将:
- 通过对图形模型的介绍,您将了解什么是因果关系的图形模型,关联关系如何在图中流动,以及如何使用现成的软件查询图形。
- 通过图形模型重新审视识别的概念。
- 了解阻碍识别的两个非常常见的偏差来源,它们的因果图结构,以及你可以做些什么。
3.1 关于因果关系
你有没有注意到YouTube视频中的厨师是如何出色地描述食物的?“减少酱汁,直到它达到醇和的黏稠度。”如果你只是在学习烹饪,你根本不知道这意味着什么。对于因果关系,也是一样的。假设你走进一家酒吧,听到人们在讨论因果关系(可能是经济学系旁边的酒吧)。你听到他们说收入的混淆如何使识别移民对社区失业率的影响变得困难,所以他们不得不使用 工具变量(Instrumental Variable) 。到现在为止,你可能还不明白他们在说什么。你当前只涉及到因果推断语言的皮毛,但是没关系的。你现在已经学到了一些反事实的结果和偏差;这样你就能理解因果推断要解决的关键问题了,足以理解最强大的因果推断工具:随机对照试验背后发生了什么。但这个工具并不总是可用的,或者根本不起作用(正如你将很快在 3.8 选择偏差(Selection Bias) 中看到的那样)。当你遇到更具挑战性的因果推理问题时,你还需要对因果推断语言有更广泛的理解,这样你才能正确地理解你面临的问题以及如何应对。
一门表述明确的语言能让你清晰地思考。这一章能帮助扩大你的因果推理词汇。你可以将图形模型视为因果关系的基本语言之一,用来构建因果推理问题,使识别假设更明确、甚至可视化的强大方法。图形模型让你的想法更透明。
结构因果模型(Structural Causal Model)
一些科学家使用结构因果模型(SCM)一词来指代因果推理的统一语言。这些模型由图和因果方程组成。在这里,我将主要关注SCM图形的方面。
作为进入奇妙的图形世界的起点,让我们以之前估算电子邮件对转化率的影响的例子为例,干预 T T T 是交叉销售电子邮件,结果 Y Y Y 是客户是否转换为新产品用户:
import warnings
warnings.filterwarnings('ignore')
import pandas as pd
import numpy as np
import graphviz as gr
from matplotlib import style
import seaborn as sns
from matplotlib import pyplot as plt
color=['0.3', '0.5', '0.7', '0.9']
linestyle=['-', '--', ':', '-.']
marker=['o', 'v', 'd', 'p']
pd.set_option('display.max_rows', 6)
gr.set_default_format("png");
import pandas as pd
import numpy as np
data = pd.read_csv("./data/cross_sell_email.csv")
data
| gender | cross_sell_email | age | conversion | |
|---|---|---|---|---|
| 0 | 0 | short | 15 | 0 |
| 1 | 1 | short | 27 | 0 |
| 2 | 1 | long | 17 | 0 |
| … | … | … | … | … |
| 320 | 0 | no_email | 15 | 0 |
| 321 | 1 | no_email | 16 | 0 |
| 322 | 1 | long | 24 | 1 |
323 rows × 4 columns
让我们回顾一下前一章,在这个问题中, T T T 是随机的,也就是说干预是独立于潜在结果的, ( Y 0 , Y 1 ) ⊥ T (Y_0,Y_1) \perp T (Y0,Y1)⊥T,这使得关联关系等于因果关系:
E ( Y 1 − Y 0 ) = E ( Y ∣ T = 1 ) − E ( Y ∣ T = 0 ) E(Y_1-Y_0)=E(Y|T=1)-E(Y|T=0) E(Y1−Y0)=E(Y∣T=1)−E(Y∣T=0)
重要的是,绝对没有办法通过观察数据来判断独立性假设是否成立。你只能这么说你有干预赋值机制的信息。也就是说,你知道邮件是随机的。
3.1.1 可视化因果关系
你可以将行业知识编码到一个图形中,图形能捕捉你关于什么原因导致什么结构的信念。比如在这个简单的例子中,你相信交叉销售电子邮件会导致用户转化,你还认为你测量的其他变量(年龄和性别)也会导致转化。在图形中,你还可以添加你没有测量的变量。我们通常用字母 U U U 来表示它们,它们是被忽略的。可能有许多未观察到的变量会导致转换(如客户收入、社会背景、你的产品如何吸引不同人群、公司所在城市)。但由于你不度量它们,所以可以将所有内容捆绑到一个节点 U U U 中,该节点表示所有未度量的变量。最后,你可以添加一个随机节点指向 T T T,表示你知道交叉销售电子邮件是随机的。
DAG
你可能会发现人们把因果图称为DAG。这个缩略词代表有向无环图。有向图告诉你这些边是有方向的,这与无向图不同,比如社交网络。无环部分告诉你,图形没有循环。因果图通常是有向和无环的,因为因果关系是不可逆的。
你可以使用graphviz将你的信念添加到图形中,直接看到它们:
import graphviz as gr
g_cross_sell = gr.Digraph()
g_cross_sell.edge("U", "conversion")
g_cross_sell.edge("U", "age")
g_cross_sell.edge("U", "gender")
g_cross_sell.edge("rnd", "cross_sell_email")
g_cross_sell.edge("cross_sell_email", "conversion")
g_cross_sell.edge("age", "conversion")
g_cross_sell.edge("gender", "conversion")
g_cross_sell
图中的每个节点都是一个随机变量。您可以使用箭头或边来显示一个变量是否影响另一个变量。在这个图形模型中,你说电子邮件引起了转化, U U U 影响了年龄、转化、性别,等等。这种图形模型的语言将帮助你澄清对因果关系的思考,因为它使你对世界如何工作的信念更加明确。或许你会觉得这是多么不切实际,毕竟你不可能对这个数据中常见的数百个变量进行编码,请放心,你不需要这样做。在实践中,你可以通过捆绑节点从根本上简化事情,同时保持你试图传达的一般因果故事。例如,你可以把前面的图和可观察变量捆绑到一个节点 X X X 中。因为这些变量都是由 U U U 引起,然后导致转化的,将这些变量聚合起来,使你的因果故事保持完整。
此外,当你声明一些随机化或被干预的变量时,你可以删除这些变量所有传入的箭头:
# rankdir:LR layers the graph from left to right
g_cross_sell = gr.Digraph(graph_attr={"rankdir": "LR"})
g_cross_sell.edge("U", "conversion")
g_cross_sell.edge("U", "X")
g_cross_sell.edge("cross_sell_email", "conversion")
g_cross_sell.edge("X", "conversion")
g_cross_sell
在这里有趣的是,DAG可能没有包含最重要的信息:如果从一个变量到另一个变量之间没有边连接,表示假设这两个变量之间没有直接因果关系。例如,在前面的图形中,你假设没有任何原因影响干预和结果。
就像你学习的每一种语言一样,你可能觉得不考虑这个问题是不完全合理的。话虽如此,但如果我可以扔给你一堆规则和最佳实践来表示图形中的变量之间的因果关系,可能是最低效的学习方式。相反,我的计划是让你接触大量的例子,随着时间的推移,你会掌握图形的窍门。现在,我只想让你记住,图形是理解为什么关联关系不是因果关系的一个非常强大的工具。
3.1.2 顾问价有所值吗?
为了了解DGA的力量,让我们考虑一个更有趣的例子。在这个例子中,干预不是随机的。假设你是一家公司的经理,正在考虑是否要引进一些顶尖的顾问。你知道他们很贵,但你也知道他们有与业内最好的公司合作的专业知识。更复杂的是,你不确定顶级顾问是真的会改善你的业务,还是只有负担得起这些顾问的企业才具备很强的盈利能力,导致顾问的存在与强劲的业务表现相关。如果有人能随机安排咨询顾问,那就太棒了,因为这样一来,回答这个问题就显得微不足道了。但当然,没有这种奢侈的情况,所以你必须想出其他的办法。正如你现在可能看到的,这是一个从关联关系中理清因果关系的问题。为了理解它,你可以将你对它的因果机制的信念编码在一个图形中:
g_consultancy = gr.Digraph(graph_attr={"rankdir": "LR"})
g_consultancy.edge("U1", "profits_next_6m")
g_consultancy.edge("U2", "consultancy")
g_consultancy.edge("U3", "profits_prev_6m")
g_consultancy.edge("consultancy", "profits_next_6m")
g_consultancy.edge("profits_prev_6m", "consultancy")
g_consultancy.edge("profits_prev_6m", "profits_next_6m")
g_consultancy
请注意,我是如何向每个变量添加节点 U U U 以表示有其他我们无法衡量的因素在影响这些变量。由于图形通常代表随机变量,因此可以预料一个随机因素将影响 U U U 所代表的所有变量。然而,这些外部变量并不能为我的因果故事添加任何有用信息,所以我可以省略它们:
g_consultancy = gr.Digraph(graph_attr={"rankdir":"LR"})
g_consultancy.edge("consultancy", "profits_next_6m")
g_consultancy.edge("profits_prev_6m", "consultancy")
g_consultancy.edge("profits_prev_6m", "profits_next_6m")
g_consultancy
这里,我的意思是,一家公司过去的业绩导致该公司聘请了一流的顾问。如果公司做得很好,它可以支付昂贵的服务。如果公司做得不好,那就做不到。因此,过去的业绩(这里用过去的利润来衡量)决定了一家公司聘请顾问的概率。请记住,这种关系不一定是决定性的。我只是说,做得好的公司更有可能聘请一流的顾问。
不仅如此,过去6个月表现良好的公司很可能在未来6个月也表现良好。当然,这并不总是会发生,但平均而言,它确实会发生,这就是为什么从过去的表现到未来的表现之间也有一条边。最后,我还在咨询和公司的未来业绩之间增加了边。你的目标是了解这种关系的优势,也就是你关心的因果关系:咨询真的能提高公司业绩吗?
回答这个问题并不简单,因为咨询与未来业绩之间存在两个联系来源。一个是因果关系,另一个不是。为了理解和理清它们,你首先需要快速查看因果图中的关联是如何流动的。
3.2 图形模型速成课程
关于图形模型,学校都会安排一整个学期的学习时长。无论如何,如果你想深入研究图形模型,它将对你理解因果推理非常有益。但是,就本书的目的而言,理解图形模型需要什么样的独立性和条件独立性假设 就够了。正如你将看到的,关联在图形模型中流动就像水在小溪中流动一样。你可以停止或启用该流,这取决于您如何处理图中的变量。为了理解这一点,让我们研究一些常见的图形结构和示例。它们简单易懂,但是将它们作为构建块来理解图形模型上的关联流、独立性和条件独立性的一切,足够了。
3.2.1 链(Chains)
首先,看看这个非常简单的图形——链。这里T影响M, M影响Y。有时可以将中间节点称为中介,因为它调解了T和Y之间的关系:
g = gr.Digraph(graph_attr={"rankdir": "LR"})
g.edge("T", "M")
g.edge("M", "Y")
g.node("M", "M")
g.edge("causal knowledge", "solve problems")
g.edge("solve problems", "job promotion")
g
在第一个图中,因果关系只在箭头方向流动,但关联关系是双向流动的。举一个更具体的例子,假设了解因果推理提高了你解决问题的能力,解决问题增加了你获得晋升的机会。因此,因果知识会提高你解决问题的能力,这反过来又会使你获得升职。你可以说,工作晋升依赖于因果知识。专业知识越多,你获得晋升的机会就越大。此外,你晋升的机会越大,你拥有因果知识的机会就越大。否则,就很难得到晋升。换句话说,工作晋升与因果推断专业知识之间存在关联,就像因果推断专业知识与工作晋升之间存在关联一样,尽管其中只有一个方向是因果的。当两个变量相互关联时,你可以说它们是相关的,也可以说它们不是独立的:
T ⊥̸ Y T \not\perp Y T⊥Y
现在,让我们保持中介变量固定,也就是你可以只看解决问题能力为M的人。正式地说,你可以说你以M为条件,在这种情况下,依赖被阻断了。因此,T和Y在给定M的情况下是独立的,你可以用数学方法表示为:
T ⊥ Y ∣ M T \perp Y|M T⊥Y∣M
为了表明我们正在对一个节点进行条件限制,我们将其标上阴影:
g = gr.Digraph(graph_attr={"rankdir": "LR"})
g.edge("T", "M")
g.edge("M", "Y")
g.node("M", "M")
g.node("M", color="lightgrey", style="filled")
g.edge("causal knowledge", "solve problems")
g.edge("solve problems", "job promotion")
g.node("solve problems", color="lightgrey", style="filled")
g
如果你观察一群解决问题能力相同的人,知道哪些人擅长因果推断并不能提供任何关于他们获得升职机会的进一步信息。用数学术语来说:
E ( P r o m o t i o n ∣ S o l v e p r o b l e m s , C a u s a l k n o w l e d g e ) = E ( P r o m o t i o n ∣ S o l v e p r o b l e m s ) E(Promotion|Solve problems,Causal knowledge)=E(Promotion|Solve problems) E(Promotion∣Solveproblems,Causalknowledge)=E(Promotion∣Solveproblems)
反之亦然,一旦我知道你有多擅长解决问题,了解你的晋升状况并不能让我进一步了解你有多大可能知道因果推断。
一般来说,如果你有一个像上面图中那样的链,当你对中介变量M施加条件时,从T到Y的路径中的关联流就会被阻塞,也就是:
T ⊥̸ Y T ⊥ Y ∣ M T \not\perp Y \\ T \perp Y|M T⊥YT⊥Y∣M
3.2.2 分叉(Forks)
分叉结构:同一个变量影响图形下方的两个其他变量。在分叉中,关联通过箭头向后流动:
g = gr.Digraph()
g.edge("X", "Y")
g.edge("X", "T")
g.node("X", "X")
g.edge("statistics", "causal inference")
g.edge("statistics", "machine learning")
g
例如,假设你的统计学知识让你对因果推断和机器学习有了更多的了解。然而,知道因果推断对机器学习没有帮助,反之亦然,所以这些变量之间没有边。
这张图告诉你,如果你不知道一个人的统计知识水平,那么知道他擅长因果推断会让他更有可能擅长机器学习,即使因果推断对你的机器学习没有帮助。这是因为即使你不知道一个人的统计知识水平,你也可以从他们的因果推断知识中推断出来。如果他们擅长因果推断,那么他们可能擅长统计学,这使得他们更有可能擅长机器学习。分叉末端的变量并不互为因果,但是会一起变化,只是因为它们都是由同一件事引起的。在因果推断的文献中,当我们在干预和结果之间有一个共同的原因时,我们称这个共同原因为混杂因子(Confounder)。
分叉结构在因果推断中非常重要。你知道科技招聘人员有时会要求你解决一些你申请的岗位中可能永远不会遇到的问题,比如他们让你对二叉树进行倒转或者使用Python统计重复的元素。这件事情本质上利用了下图中通过分叉结构的关联流体现的事实:
g = gr.Digraph()
g.edge("good programmer", "can invert a binary tree")
g.edge("good programmer", "good employee")
g
招聘人员知道优秀的程序员往往是表现最好的人。但是当他们面试你的时候,他们不知道你是不是一个好的程序员,所以他们会问你一个只要你是好程序员就有能力回答的问题。这个问题不一定是你在应聘的工作中会遇到的问题,它只是表明你是否是一个好的程序员。如果你能回答这个问题,你很可能是一个优秀的程序员,这意味着你也很可能是一个优秀的员工。
现在,让我们假设招聘人员已经知道你是一名优秀的程序员。也许他们从你以前的公司获取了有关你的信息,或者你有一个令人印象深刻的学位。在这种情况下,知道你是否能回答申请过程中的问题并不能进一步说明你是否会成为一名好员工。使用技术术语来表述就是,现在以你已经是一名好程序员为条件,回答问题和成为一名好员工是独立的。
更一般地说,如果你有一个分叉结构,共享一个共同原因的两个变量是不独立的,但当你把共同原因作为条件时,它们是独立的,也就是:
T ⊥̸ Y T ⊥ Y ∣ X T \not\perp Y \\ T \perp Y|X T⊥YT⊥Y∣X
3.2.3 不道德(Immorality)与碰撞器(Collider)
不道德(Immorality)(不用怀疑,这是一个技术术语)是指两个没有直接关系的节点共享一个子节点。另一种说法是两个变量共享一个共同的效果。这种共同的效果通常被称为碰撞器(Collider),因为两个箭头在它上面发生碰撞:
g = gr.Digraph()
g.edge("Y", "X")
g.edge("T", "X")
g.edge("statistics", "job promotion")
g.edge("flatter", "job promotion")
g
在不道德的情况下,两个父节点是相互独立的。但如果你以共同效果为条件,它们就会互相依赖。例如,考虑有两种方法可以获得升职:你可以擅长统计,也可以奉承你的老板。如果我不以你的晋升为条件,也就是说,我不知道你是否会得到晋升,那么你的统计和奉承水平是独立的。换句话说,知道你有多擅长统计学,并不能说明你有多擅长奉承你的老板。另一方面,如果你确实得到了晋升,了解你的统计水平就能告诉我你的奉承程度。如果你不擅长统计,但确实获得了晋升,你可能会很擅长奉承你的老板。否则,你升职的可能性就很小了。相反,如果你擅长统计,你更有可能不擅长奉承,因为擅长统计已经解释了你的晋升。这种现象有时被称为淡化(Explaining Away),因为一个原因已经解释了结果,使另一个原因不太可能。
作为一般规则,碰撞器的条件作用打开关联路径,使变量相互依赖。没有条件作用,它就关闭了,也就是:
{ T ⊥ Y T ⊥̸ Y ∣ X \begin{cases} T \perp Y \\ T \not\perp Y|X \end{cases} {T⊥YT⊥Y∣X
重要的是,如果你不是在碰撞器上设置条件,而是在碰撞器的效果上设置条件(直接或间接),那你可以打开相同的依赖路径。继续我们的例子,现在让我们假设得到升职大大增加了你的薪水,这就给了你下一个图形:
3.2.5 使用Python进行图形查询
看下面的图形:
g = gr.Digraph(graph_attr={"rankdir": "LR"})
g.edge("C", "A")
g.edge("C", "B")
g.edge("D", "A")
g.edge("B", "E")
g.edge("F", "E")
g.edge("A", "G")
g
把这个图输入到Python库中,回答有关它的问题就会变得非常容易。但在你这么做之前,试着自己回答以下问题,消化刚刚学到的概念:
- D和C是相互依赖的吗?
- 给定A后,D和C是相互依赖的吗?
- 给定G后,D和C是相互依赖的吗?
- A和B是相互依赖的吗?
- 给定C后,A和B是相互依赖的吗?
- G和F是相互依赖的吗?
- 给定E后,G和F是相互依赖的吗?
现在,看看你是否做对了,你可以把这个图输入到networkx的有向图中。networkx是一个处理图形模型的库,它有一堆方便的算法,可以帮助你检查这个图:
import networkx as nx
model = nx.DiGraph([
("C", "A"),
("C", "B"),
("D", "A"),
("B", "E"),
("F", "E"),
("A", "G"),
])
作为开始,让我们以D和C为例,它们构成了你之前看到的不道德结构,A是一个碰撞器。根据不道德结构的独立性规则,D和C是独立的。你也知道如果你在碰撞器A上设置条件,它们之间就会产生关联。d_separated方法告诉你图中两个变量之间是否存在关联(d-separation是表示图中两个变量之间独立性的另一种方法)。要对一个变量设置条件,您可以将其添加到观察集。例如,在给定A的情况下,要检查D和C是否相关,你可以设置d_separated方法的第四个参数z={“A”}:
print("Are D and C dependent?")
print(not(nx.d_separated(model, {"D"}, {"C"}, {})))
print("Are D and C dependent given A?")
print(not(nx.d_separated(model, {"D"}, {"C"}, {"A"})))
print("Are D and C dependent given G?")
print(not(nx.d_separated(model, {"D"}, {"C"}, {"G"})))
Are D and C dependent?
False
Are D and C dependent given A?
True
Are D and C dependent given G?
True
接下来,注意D, A和G组成了一个链。你知道关联是在一个链中流动的,所以D不是独立于G的。但是,如果你把中介变量A作为条件,你就阻断了关联的流动:
print("Are G and D dependent?")
print(not(nx.d_separated(model, {"G"}, {"D"}, {})))
print("Are G and D dependent given A?")
print(not(nx.d_separated(model, {"G"}, {"D"}, {"A"})))
Are G and D dependent?
True
Are G and D dependent given A?
False
您需要检查的最后一个结构是分叉。你可以看到A, B和C形成了一个分叉,C是A和B的共同原因。你知道这种关联通过一个分叉流动,所以A和B不是独立的。然而,如果你设定共同原因为条件,关联的路径被阻断:
print("Are A and B dependent?")
print(not(nx.d_separated(model, {"A"}, {"B"}, {})))
print("Are A and B dependent given C?")
print(not(nx.d_separated(model, {"A"}, {"B"}, {"C"})))
Are A and B dependent?
True
Are A and B dependent given C?
False
最后,让我们把所有的东西放在一起,谈谈G和F,它们之间有关联吗?让我们从G开始,你知道G和E之间的关联流,因为它们在一个分叉中。然而,关联在碰撞器E处停止,这意味着G和F是独立的。然而,如果你以E为条件,关联开始通过碰撞器,路径打开,连接G和F:
print("Are G and F dependent?")
print(not(nx.d_separated(model, {"G"}, {"F"}, {})))
print("Are G and F dependent given E?")
print(not(nx.d_separated(model, {"G"}, {"F"}, {"E"})))
Are G and F dependent?
False
Are G and F dependent given E?
True
这太棒了。你不仅学习了图中的三种基本结构,还了解了如何使用现成的算法来检查图中的独立性。但这和因果推断有什么关系呢?是时候回到我们在本章开头探讨的问题了。回想一下,我们试图了解聘请昂贵的顶尖顾问对企业绩效的影响,我们将其描述为下图:
你可以使用你新获得的技能来看看为什么在这个图表中关联关系不是因果关系。注意,在这个图中有一个分叉结构。因此,咨询公司与公司未来业绩之间存在两种关联流:直接因果路径和被共同原因混淆的非因果路径。后一种被称为后门路径(Backdoor Path)。图中混杂后门路径的存在表明,观察到的咨询公司和公司业绩之间的关联不能完全归因于因果关系。
3.3 重新识别
到目前为止,在没有随机化的情况下,我一直用来解释为什么很难找到因果关系的论点是,干预和未干预的分析单元之间没有可比性。例如,雇佣顾问的公司通常比那些不雇佣昂贵顾问的公司有更好的历史表现。这导致了你之前见过的那种偏差:
E ( Y ∣ T = 1 ) − E ( Y ∣ T = 0 ) = E ( Y 1 − Y 0 ∣ T = 1 ) ⏟ A T T + ( E ( Y 0 ∣ T = 1 ) − E ( Y 0 ∣ T = 0 ) ) ⏟ − B i a s 1 E(Y|T=1)-E(Y|T=0)=\underbrace{E(Y_1-Y_0|T=1)}_{ATT}+\underbrace{(E(Y_0|T=1)-E(Y_0|T=0))}_{-Bias_1} E(Y∣T=1)−E(Y∣T=0)=ATT E(Y1−Y0∣T=1)+−Bias1 (E(Y0∣T=1)−E(Y0∣T=0))
既然你已经学习了因果图,你就可以更准确地了解这种偏差的本质,更重要的是,你可以明白你可以做些什么来消除它。在图形模型中,识别与独立性密切相关。如果你有一个图形描述了干预、结果、其他相关变量之间的因果关系,你可以把识别看作是在图形中分离干预和结果之间因果关系的过程。在识别阶段,你将基本上关闭所有不希望的关联流。
以咨询公司的图形为例。正如你之前看到的,在干预和结果之间有两条关联路径,但其中只有一条是因果关系。你可以通过创建一个因果图来检查是否有偏差,这个因果图和原来的图一样,但是去掉了因果关系。如果在这张图中,干预和结果仍然有联系,那一定是由于非因果路径,这表明存在偏差:
consultancy_sev = gr.Digraph(graph_attr={"rankdir": "LR"})
consultancy_sev.edge("profits_prev_6m", "profits_next_6m")
consultancy_sev.edge("profits_prev_6m", "consultancy")
consultancy_sev
consultancy_model_severed = nx.DiGraph([
("profits_prev_6m", "profits_next_6m"),
("profits_prev_6m", "consultancy"),
# ("consultancy", "profits_next_6m"), # causal relationship removed
])
not(nx.d_separated(consultancy_model_severed,
{"consultancy"}, {"profits_next_6m"}, {}))
True
这些关联的非因果流被称为后门路径。为了识别 T T T 和 Y Y Y 之间的因果关系,你需要关闭这些后门路径,这样就只剩下因果路径了。在咨询公司的例子中,你知道,给公共原因——公司历史表现设置条件,就关闭了后门路径:
g_consultancy = gr.Digraph(graph_attr={"rankdir":"LR"})
g_consultancy.edge("profits_prev_6m", "profits_next_6m")
g_consultancy.edge("profits_prev_6m", "consultancy")
g_consultancy.edge("consultancy", "profits_next_6m")
g_consultancy.node("profits_prev_6m", color="lightgrey", style="filled")
g_consultancy
你刚刚看到,对profits_prev_6m设置条件阻碍了干预、咨询和结果(公司未来业绩)之间的非因果关联流。因此,如果你观察一组过去表现相似的公司,在这组公司内部,比较那些聘请顾问的公司和那些没有聘请顾问的公司的未来表现,差异可以完全归因于顾问。这很直观,对吧?被干预的公司(聘请顾问的公司)和未干预的公司未来表现的差异是:1)由于干预本身,2)由于聘请顾问的公司往往从一开始就做得很好。如果你比较的干预过的公司和没有干预过的公司一直以来表现都一样好,第二个差异的来源就消失了。
当然,就像因果推断中的所有东西一样,你在这里做的是一个假设。具体来说,你假设所有干预和结果之间的非因果联系的来源都是由于你可以测量和设置条件的共同原因。这与你之前看到的独立性假设非常相似,但以其更弱的形式表示:
( Y 0 , Y 1 ) ⊥ T ∣ X (Y_0,Y_1) \perp T|X (Y0,Y1)⊥T∣X
这个条件独立假设(CIA)指出,如果你比较协变量 X X X 水平相同的单元(即公司),它们的潜在结果平均来说是相同的。另一种说法是,如果你观察具有相同协变量 X X X 的单元,那么干预似乎是随机的。
CIA的众多名称
CIA渗透到了很多因果推断研究,它有很多名字,比如可忽略性(Ignorability),外生性(Exogeneity),或可交换性(Exchangeability)。
CIA还提出了一种非常简单的方法,从数据中可观察到的量来确定因果关系。如果干预在以 X X X 划分的各组内看起来是随机的,你所需要做的就是在每个定义的组内比较干预和未干预的单元,并使用组的大小作为权重计算平均结果:
A T E = E X ( E ( Y ∣ T = 1 ) − E ( Y ∣ T = 0 ) ) ATE=E_X(E(Y|T=1)-E(Y|T=0)) ATE=EX(E(Y∣T=1)−E(Y∣T=0))
A T E = ∑ x { ( E ( Y ∣ T = 1 , X = x ) − E ( Y ∣ T = 0 , X = x ) ) P ( X = x ) } = ∑ x { E ( Y ∣ T = 1 , X = x ) P ( X = x ) − E ( Y ∣ T = 0 , X = x ) P ( X = x ) } \begin{aligned} ATE&=\sum_x{\{(E(Y|T=1,X=x)-E(Y|T=0,X=x))P(X=x)\}} \\ &=\sum_x{\{E(Y|T=1,X=x)P(X=x)-E(Y|T=0,X=x)P(X=x)\}} \end{aligned} ATE=x∑{(E(Y∣T=1,X=x)−E(Y∣T=0,X=x))P(X=x)}=x∑{E(Y∣T=1,X=x)P(X=x)−E(Y∣T=0,X=x)P(X=x)}
这就是所谓的调整公式或条件原则。它说,如果你设定条件或执行控制,平均干预效果可以被识别为干预组和对照组之间的组内差异的加权平均值。同样,如果设定条件阻止了图中通过非因果路径的关联流,那么因果量,比如ATE,就可以被识别,这意味着你可以从可观测数据中计算它。通过混杂因子的调整来关闭后门路径的过程得到了一个令人难以置信的创造性名称:后门调整(Backdoor Adjustment)。
3.5 正值性假设(Positivity Assumption)
调整公式也凸显了积极因素的重要性。由于你是在X上求干预和结果之间的差异的平均值,必须确保,对于所有按照X设定的组,在干预组中有一些单元,在对照组中也有一些单元,否则差异是无法定义的。更正式的说法是,干预的条件概率需要严格为正且小于1: 1 > P ( T ∣ X ) > 0 1>P(T|X)>0 1>P(T∣X)>0。当干预的条件概率正值性不满足时,仍然可以继续识别,但可能导致你做出危险的推断。
Positivity的众多名称
由于积极假设在因果推断中也很流行,它也有很多名字,比如共同支持(Common Support)或重叠(Overlap)。
3.6 一个在数据中进行识别的案例
这些概念可能有点抽象,让我们看看实际在数据是如何使用这些概念的。假设你收集了6家公司的数据,其中3家在过去6个月里利润很低(100万美元),3家利润很高。正如你所怀疑的那样,高利润公司更有可能聘请顾问,三家高利润公司中有两家聘请了顾问,而三家低利润公司中只有一家聘请了顾问(如果低样本让你感到困扰,请假装这里的每个数据点实际上代表了10000家公司):
df = pd.DataFrame(dict(
profits_prev_6m=[1.0, 1.0, 1.0, 5.0, 5.0, 5.0],
consultancy=[0, 0, 1, 0, 1, 1],
profits_next_6m=[1, 1.1, 1.2, 5.5, 5.7, 5.7],
))
df
| profits_prev_6m | consultancy | profits_next_6m | |
|---|---|---|---|
| 0 | 1.0 | 0 | 1.0 |
| 1 | 1.0 | 0 | 1.1 |
| 2 | 1.0 | 1 | 1.2 |
| 3 | 5.0 | 0 | 5.5 |
| 4 | 5.0 | 1 | 5.7 |
| 5 | 5.0 | 1 | 5.7 |
如果你简单地比较那些聘请顾问的公司和那些没有聘请顾问的公司的profits_next_6m,你会得到1.66M的利润差异:
(df.query("consultancy==1")["profits_next_6m"].mean()
- df.query("consultancy==0")["profits_next_6m"].mean())
1.666666666666667
但你清楚这并不是咨询对公司业绩的因果影响,因为过去表现较好的公司在聘请咨询公司的集团中所占比例过高。为了对顾问的影响做出公正的估计,你需要研究过去表现类似的公司。正如你所看到的,这产生了更温和的结果:
avg_df = (df
.groupby(["consultancy", "profits_prev_6m"])
["profits_next_6m"]
.mean())
avg_df.loc[1] - avg_df.loc[0]
profits_prev_6m
1.0 0.15
5.0 0.20
Name: profits_next_6m, dtype: float64
如果你对这些效果进行加权平均,其中权重是每组的大小,你最终会得到ATE的无偏估计。在这里,由于两组的大小相同,结果只是一个简单的平均值,ATE=175000。因此,如果你是一个决定是否雇佣顾问的管理者,你看到了上述数据,你可以得出顾问对未来利润的影响约为17.5万美元。当然,为了做到这一点,你必须求助于CIA。也就是说,你必须假设过去的表现是招聘顾问和未来表现的唯一共同原因。
你刚刚通过了一个完整的例子把你对因果机制的信念编码成一个图表,并使用这个图表找出你需要设定条件的变量,以便估算ATE,即使没有干预不是随机的。然后根据调整公式和条件独立性,你看到了一些数据是什么样子的,并估算了ATE,。这里使用的工具是相当普遍的,告诉你许多因果问题。不过,我认为我们还没有结束。一些图形结构,以及它们所包含的偏差,比其他图形结构更为常见。有必要把它们通读一遍,这样你就可以开始对因果推断过程中面临的困难有一些感觉。
前门调整(Front Door Adjustment)
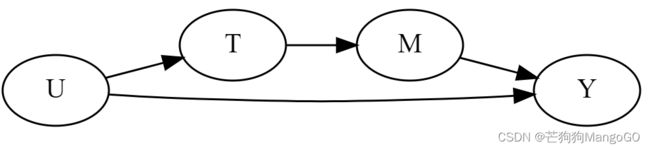
后门调整并不是识别因果关系的唯一可行策略。人们可以利用因果机制的知识,通过前门也能识别因果效果,即使存在未测量的共同原因:
g = gr.Digraph(graph_attr={"rankdir":"LR"})
g.edge("U", "T")
g.edge("U", "Y")
g.edge("T", "M")
g.edge("M", "Y")
g
使用这种策略,你必须能够识别干预对中介的影响,以及中介对结果的影响。然后,干预对结果的影响的识别就变成了这两种影响的结合。然而,在科技行业,很难找到应用场景对应的这种图形是可信的,这就是为什么前门调整不那么受欢迎。
3.7 混杂偏倚(Confounding Bias)
我们到目前为止一直在讨论的偏差产生的第一个重要原因是混杂。当有一个开通的后门路径通过非因果的关联流时,混杂(Confounding)就会发生,通常是因为干预和结果共享一个共同原因。例如,假设你在人力资源部门工作,你想知道你的新管理培训项目是否能提高雇主的雇佣。然而,由于培训是可选的,你认为只有那些已经做得很好的经理才会参加这个项目,而那些最需要它的人反而不会。当你衡量接受培训的经理手下的团队的被雇佣情况时,它比没有参加培训的经理手下的团队的被雇佣情况要高得多。但很难知道这其中有多少是因果关系。干预和结果之间有一个共同原因,而不考虑因果关系的话,它们将一起变化。
为了确定这种因果关系,你需要关闭干预和结果之间的所有后门路径。如果你这样做了,剩下的唯一效果就是 T → Y T \rightarrow Y T→Y 的直接效果了。在我们的例子中,您可以干预之前以某种方式限制经理的能力。在这种情况下,培训前的经理能力将在干预组和对照组内部保持不变,结果的差异将只取决于培训。简单地说,为了调整混淆偏差,你调整干预和结果的共同原因:
g = gr.Digraph(graph_attr={"rankdir":"LR"})
g.edge("X", "T")
g.edge("X", "Y")
g.edge("T", "Y")
g.edge("Manager Quality", "Training"),
g.edge("Manager Quality", "Engagement"),
g.edge("Training", "Engagement")
g
不幸的是,不可能总是针对所有的共同原因进行调整。有时,有一些原因你是无法衡量的,管理者能力就是其中之一。尽管付出了所有努力,我们仍然没有找到衡量管理能力的方法。如果你不能观测经理的能力,那么你就不能以它为条件,培训对雇佣的影响是无法识别的。
3.7.1 代理混杂因子(Surrogate Confounding)
在某些情况下,由于未测量的混杂因子,您无法关闭所有的后门路径。在下面的例子中,再一次,经理能力影响他们对培训的选择和团队的雇佣。因此,干预(培训)和结果(团队的雇佣情况)之间的关系存在混杂。但你不能限制混淆因子,因为它是不可测量的。在这种情况下,由于混杂偏差,干预对结果的因果效应无法识别。然而,你还有其他可测量的变量,它们可以作为混杂因子(经理的能力)的代理。这些变量并不在后门路径中,但对它们进行控制将有助于减少偏差(尽管不会消除偏差)。这些变量有时被称为代理混杂因子。
在这个例子中,你不能衡量经理的能力,但你可以衡量其原因,比如经理的任期或教育水平;以及它的一些影响,比如团队的自然减员或业绩。控制这些代理变量不足以消除偏见,但它肯定有帮助:
g = gr.Digraph()
g.edge("X1", "U")
g.edge("U", "X2")
g.edge("U", "T")
g.edge("T", "Y")
g.edge("U", "Y")
g.edge("Manager Quality", "Team's Attrition")
g.edge("Manager Quality", "Team's Past Performance")
g.edge("Manager's Tenure", "Manager Quality")
g.edge("Manager's Education Level", "Manager Quality")
g.edge("Manager Quality", "Training")
g.edge("Training", "Engagement")
g.edge("Manager Quality", "Engagement")
g
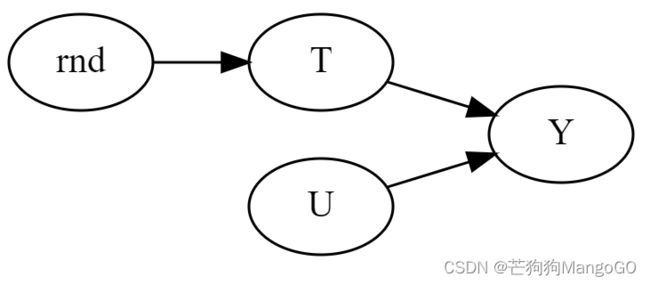
在许多重要且非常相关的研究问题中,混杂因子是一个主要课题,因为你永远无法确定是否控制了所有的混杂因子。但如果你打算在行业中主要使用因果推断,我有一个好消息要告诉你。你最感兴趣的是了解你的公司可以控制的事情的因果关系,比如价格、客户服务和营销预算,这样你就可以优化它们。在这些情况下,很容易知道混淆因子是什么,因为企业通常知道自己采取了什么干预措施,或者可以选择采取干预措施。这正是A/B测试的意义所在。当你将干预随机化时,可以从一个具有不可观察混杂因子的图形切换到一个随机化干预的图形:
g = gr.Digraph(graph_attr={"rankdir":"LR"})
g.edge("rnd", "T")
g.edge("T", "Y")
g.edge("U", "Y")
g
因此,除了看你需要以哪些变量为条件来确定效果外,你还应该问自己,你可以采取哪些可能的干预措施来改变图形,使其变成一个感兴趣的因果量可识别的图表。
当你有不可观测的混杂因子时,并不是所有的东西都丢失了。在本书第四部分中,我将介绍一些方法,可以利用数据中的时间结构来处理不可观测的混杂因素。本书第五部分将介绍相关工具变量的使用。
敏感性分析(Sensitivity Analysis)与部分识别(Partial Identification)
当你无法衡量所有的共同原因时,与其简单地放弃,不如将讨论从“我是否在衡量所有的混杂因子”转化为“未测量的混杂因子应该有多强,才能显著改变我的分析”,这就是敏感性分析背后的主要思想。要想对这个话题有一个容易理解的评论,我建议你看看Cinelli和Hazlett的论文《Making Sense of Sensitivity: extended extended Variable Bias》。
此外,即使你所关心的因果量不能被识别,你仍然可以使用可观测数据来为其设置边界。这个过程被称为
部分识别(Partial Identification),是一个活跃的研究领域。
3.8 选择偏差(Selection Bias)
如果你认为混杂偏差已经是你行走在因果推断之旅中鞋子里的一块小石头,那就等着受选择偏差的折磨吧。当你没有控制干预和结果的共同原因时,混杂偏差就会发生,而选择偏差则更多地与给共同效果和中介设置条件有关。
偏差的术语
关于偏差的名称,学术界还没有达成共识。例如,经济学家倾向于将各种各样的偏差称为选择偏差。相反,一些科学家喜欢将我所说的选择偏差进一步细分为碰撞器偏差和中介偏差。我将使用与Miguel A. Hernán和James M. Robins (Chapman & Hall/CRC)的《Causal Inference: What If》一书中相同的术语。
3.8.1 给碰撞器设定条件
考虑这样一个情况:你在一家软件公司工作,希望评估你刚刚实现的新功能的影响。为了避免任何令人困惑的偏差,你可以随机选择10%的客户获得新功能,而其余的客户则不能。你想知道这个特性是否使客户更高兴更满意。因为满意度是不能直接测量的,你可以使用净推建值(NPS)作为它的代理。为了测量NPS,你向试运营(处理)组和对照组的客户发送了一份调查,询问他们是否会推荐你的产品。当结果出现时,你会看到拥有新功能并响应调查的客户的NPS分数高于没有新功能并响应调查的客户。你能说这种差异完全是由于新功能对NPS的因果影响吗?要回答这个问题,你应该从表示这种情况的图形开始:
g = gr.Digraph(graph_attr={"rankdir": "LR"})
g.edge("T", "S")
g.edge("T", "Y")
g.edge("Y", "S")
g.node("S", color="lightgrey", style="filled")
g.edge("RND", "New Feature"),
g.edge("New Feature", "Customer Satisfaction"),
g.edge("Customer Satisfaction", "NPS"),
g.edge("Customer Satisfaction", "Response"),
g.edge("New Feature", "Response"),
g.node("Response", "Response", color="lightgrey", style="filled")
g
开门见山地说,不幸的是,答案是否定的。这里的问题是,你只能对那些回应NPS调查的人进行NPS测量。你们正在估算干预组和对照组之间的差异,同时也在对NPS调查做出回应的客户进行条件限制。尽管随机化可以让你将ATE确定为干预组和对照组之间的结果差异,但一旦你以共同效果为条件,也会引入选择偏差。要看到这一点,您可以重新创建这个图形,并删除从新特性到客户满意度的因果路径,这也关闭了到NPS的直接路径。然后,一旦你对响应设置条件,您可以检查NPS是否仍然和新功能有关联。你可以看到,这意味着两个变量之间的关联是通过非因果路径流动的,这正是偏差的含义:
nps_model = nx.DiGraph([
("RND", "New Feature"),
# ("New Feature", "Customer Satisfaction"),
("Customer Satisfaction", "NPS"),
("Customer Satisfaction", "Response"),
("New Feature", "Response"),
])
not(nx.d_separated(nps_model, {"NPS"}, {"New Feature"}, {"Response"}))
True
另请参阅
选择偏差下的因果识别是非常狡猾的。这种删除因果路径并检查干预和结果是否仍然相关的方法并不总是对选择偏差有效。不幸的是,在撰写本文时,我还不知道有任何Python库可以处理带有选择偏差的图。但您可以试试DAGitty,它在浏览器上工作,并有选择偏差下的识别算法。
为了培养你对这种偏差的直觉,让我们找回你的神力,假装你可以看到反事实结果。也就是说,你可以看到所有客户的NPS,不管这些客户是否回应了调查,控制组客户NPS为 N P S 0 NPS_0 NPS0,干预组客户NPS为 N P S 1 NPS_1 NPS1。让我们以一种我们知道真实效果的方式来模拟数据。在这里,新特性将NPS提高了0.4(对于任何业务标准来说,这都是一个很高的数字,但为了示例起见,请允许我这样做)。我们还假设新特性和客户满意度都增加了响应NPS调查的机会,就像我们在上一张图中所示的那样。有了衡量反事实的能力,如果你汇总干预组和对照组的数据,你会看到以下情况:
np.random.seed(2)
n = 100000
new_feature = np.random.binomial(1, 0.5, n)
satisfaction_0 = np.random.normal(0, 0.5, n)
satisfaction_1 = satisfaction_0 + 0.4
satisfaction = new_feature*satisfaction_1 + (1-new_feature)*satisfaction_0
nps_0 = np.random.normal(satisfaction_0, 1)
nps_1 = np.random.normal(satisfaction_1, 1)
nps = new_feature*nps_1 + (1-new_feature)*nps_0
responded = (np.random.normal(0 + new_feature + satisfaction, 1) > 1).astype(int)
tr_df = pd.DataFrame(dict(new_feature=new_feature,
responded=responded,
nps_0=nps_0,
nps_1=nps_1,
nps=nps))
tr_df_measurable = pd.DataFrame(dict(new_feature=new_feature,
responded=responded,
nps_0=np.nan,
nps_1=np.nan,
nps=np.where(responded, nps, np.nan)))
tr_df.groupby("new_feature").mean()
| responded | nps_0 | nps_1 | nps | |
|---|---|---|---|---|
| new_feature | ||||
| 0 | 0.183715 | -0.005047 | 0.395015 | -0.005047 |
| 1 | 0.639342 | -0.005239 | 0.401082 | 0.401082 |
首先,请注意,拥有新特性的用户中有63%回应了NPS的调查,而对照组中只有18%回应了它。接下来,如果您查看干预行和对照行,你将看到从 N P S 0 NPS_0 NPS0 到 N P S 1 NPS_1 NPS1 增加了0.4。这仅仅意味着新特性对两组的影响都是0.4。最后,注意干预组(new_feature=1)和对照组(new_feature=0)之间的NPS差异约为0.4。同样,如果你能看到那些没有回应调查的人的NPS,你可以只比较干预组和对照组就能得到真正的ATE。
当然,在现实中,你看不到 N P S 0 NPS_0 NPS0 列和 N P S 1 NPS_1 NPS1 列。你也看不到这样的NPS列,因为只有对调查做出回应的NPS(18%的对照行和63%的干预行):
tr_df_measurable.groupby("new_feature").mean().assign(**{"nps": np.nan})
| responded | nps_0 | nps_1 | nps | |
|---|---|---|---|---|
| new_feature | ||||
| 0 | 0.183715 | NaN | NaN | NaN |
| 1 | 0.639342 | NaN | NaN | NaN |
如果进一步细分受访者的分析,你将看到那些 R e s p o n s e = 1 Response=1 Response=1 的NPS。但请注意,在该组中,干预单元和对照单元之间的差异不再是0.4,而是大约一半(0.22)。这怎么可能呢?这都是选择偏差导致的:
tr_df_measurable.groupby(["responded", "new_feature"]).mean()
| nps_0 | nps_1 | nps | ||
|---|---|---|---|---|
| responded | new_feature | |||
| 0 | 0 | NaN | NaN | NaN |
| 1 | NaN | NaN | NaN | |
| 1 | 0 | NaN | NaN | 0.314073 |
| 1 | NaN | NaN | 0.536106 |
添加回不可观察的量,你可以看到正在发生的事情(关注这里的回复调查的群体):
tr_df.groupby(["responded", "new_feature"]).mean()
| nps_0 | nps_1 | nps | ||
|---|---|---|---|---|
| responded | new_feature | |||
| 0 | 0 | -0.076869 | 0.320616 | -0.076869 |
| 1 | -0.234852 | 0.161725 | 0.161725 | |
| 1 | 0 | 0.314073 | 0.725585 | 0.314073 |
| 1 | 0.124287 | 0.536106 | 0.536106 |
最初,干预组和对照组在基线满意度 Y 0 Y_0 Y0 方面是可比的。但一旦你以那些回应调查的人为条件,干预组就有了较低的基线满意度 E ( Y 0 ∣ T = 0 , R = 1 ) > E ( Y 0 ∣ T = 1 , R = 1 ) E(Y_0|T=0,R=1)>E(Y_0|T=1,R=1) E(Y0∣T=0,R=1)>E(Y0∣T=1,R=1)。这意味着,干预组和对照组之间的平均值的简单差异并不能确定ATE:
E ( Y ∣ T = 1 , R = 1 ) − E ( Y ∣ T = 1 , R = 1 ) = E ( Y 1 − Y 0 ∣ R = 1 ) ⏟ A T E + E ( Y 0 ∣ T = 0 , R = 1 ) − E ( Y 0 ∣ T = 1 , R = 1 ) ⏟ S e l e c t i o n B i a s \begin{aligned} E(Y|T=1,R=1)-E(Y|T=1,R=1)&=\underbrace{E(Y_1-Y_0|R=1)}_{ATE}\\ &+\underbrace{E(Y_0|T=0,R=1)-E(Y_0|T=1,R=1)}_{SelectionBias} \end{aligned} E(Y∣T=1,R=1)−E(Y∣T=1,R=1)=ATE E(Y1−Y0∣R=1)+SelectionBias E(Y0∣T=0,R=1)−E(Y0∣T=1,R=1)
如果结果,即客户满意度,影响了回复率,那么偏差项就不会是零。由于满意的客户更有可能回答NPS的调查,在这种情况下不可能进行识别。如果干预增加了满意度,那么对照组将包含更多基线满意度高于干预组的客户。这是因为干预组拥有那些很满意的人(高基线满意度)加上那些基线满意度较低、但由于干预变得更满意并回复了调查的人。
另请参阅
选择偏差是一个复杂得多的话题,我无法在这一章给出合理的解释。例如,你可以通过对结果的影响进行条件设置而产生选择偏差,即使这种影响与干预不共享结果。这种情况被称为虚拟碰撞器(Virtual Collider)。要了解更多关于它的信息,我强烈建议你看看Carlos Cinelli等人的论文《A Crash Course in Good and Bad Controls》。这篇论文涵盖了本章及更多内容,也是用清晰的语言写的,易于阅读。
3.8.2 选择偏差的调整
不幸的是,纠正选择偏差并不是简单的事情。在我们讨论的例子中,即使是随机对照试验,ATE也无法确定,原因很简单,因为一旦你以那些回应调查的人为条件,你就无法关闭新特性和客户满意度之间的非因果关联流。要取得一些进展,你需要做出进一步的假设,这就是图形模型开始发光的地方。它让这些假设非常明确、透明。
例如,你需要假设结果不会影响选择。在我们的例子中,这意味着客户满意度不会导致客户更多或更少地回答调查。相反,你将有一些其他可观察变量,这些变量影响选择和结果。例如,导致客户回应调查的唯一事情可能是他们在应用程序和新功能上花费的时间。在这种情况下,干预组和对照组之间的非因果关联在应用程序中随着时间的推移而流动:
g = gr.Digraph()
g.edge("U", "X")
g.edge("X", "S")
g.edge("U", "Y")
g.edge("T", "Y")
g.edge("T", "S")
g.node("S", color="lightgrey", style="filled")
g.edge("New Feature", "Customer Satisfaction"),
g.edge("Unknown Stuff", "Customer Satisfaction"),
g.edge("Unknown Stuff", "Time in App"),
g.edge("Time in App", "Response"),
g.edge("New Feature", "Response"),
g.node("Response", "Response", color="lightgrey", style="filled")
g
只有专家知识才能告诉我们这个假设有多强。但如果它是正确的,一旦你在应用程序中控制时间,新功能对满意度的影响就可以识别了。
同样,你在这里y也应用了调整公式。你只是将数据细分为 X X X 定义的组,以便干预组和对照组在这些细分组中具有可比性。然后,你只需计算干预组和对照组之间的组内差异的加权平均值,同样也是使用每个组的大小作为权重。只是现在,你在做所有这些的同时,也在对选择变量设置条件:
A T E = ∑ x { ( E ( Y ∣ T = 1 , R = 1 , X ) − E ( Y ∣ T = 0 , R = 1 , X ) ) P ( X ∣ R = 1 ) } ATE=\sum_x{\{(E(Y|T=1,R=1,X)-E(Y|T=0,R=1,X))P(X|R=1)\}} ATE=x∑{(E(Y∣T=1,R=1,X)−E(Y∣T=0,R=1,X))P(X∣R=1)}
一般来说,为了调整选择偏差,你必须调整导致选择的任何原因,你还必须假设结果或干预都不会直接影响选择或与选择有一个隐藏的共同原因。例如,下面的图就有选择偏差,因为对S设置条件在T和Y之间打开了一条非因果关联路径:
g = gr.Digraph(graph_attr={"rankdir": "LR"})
g.edge("X1", "U")
g.edge("U", "X2")
g.edge("X5", "S")
g.edge("U", "Y",style="dashed")
g.edge("U", "S",style="dashed")
g.edge("U", "X3")
g.edge("X3", "S")
g.edge("Y", "X4")
g.edge("X4", "S")
g.edge("T", "X5")
g.edge("T", "Y")
g.edge("T", "S", style="dashed")
g.node("S", color="lightgrey", style="filled")
g
您可以通过调整表达(explain)选择的可测量变量X3、X4、X5来关闭其中两条路径。然而,有两种路径你不能关闭(如虚线所示): Y → S ← T Y \rightarrow S \leftarrow T Y→S←T 和 T → S ← U → Y T \rightarrow S \leftarrow U \rightarrow Y T→S←U→Y。这是因为干预直接影响选择,结果与选择有一个隐藏的共同原因。你可以通过进一步限制X2和x1来减轻最后一条路径的偏差(因为它们包含了U的一些变量),但这并不能完全消除偏差。
当涉及到选择偏差时,这个图形反映了一个你会遇到的更合理的情况,就像我们刚才举的例子。在这些情况下,你所能做的最好的事情就是限制表达(explain)选择的变量。这将减少偏差,但不会消除偏见,因为:1)有一些你不知道或无法衡量的事情影响选择,2)结果或干预可能直接影响选择。
生存分析中隐藏的偏差
生存分析出现在许多涉及持续时间的事件的业务应用中。例如,银行非常有兴趣了解贷款规模(贷款金额)如何增加客户对该贷款违约的概率。考虑一笔3年期贷款,客户可能在第一,第二,第三年违约,或者根本不能违约。银行的目标是了解贷款金额是如何影响 P ( D e f a u l t ∣ y r = 1 ) P(Default|yr=1) P(Default∣yr=1)、 P ( D e f a u l t ∣ y r = 2 ) P(Default|yr=2) P(Default∣yr=2)、 P ( D e f a u l t ∣ y r = 3 ) P(Default|yr=3) P(Default∣yr=3)。这里,为了简单起见,假设银行随机分配了贷款金额。请注意,只有在第1年幸免(没有违约)的客户在第2年会被观测到,只有在第1年和第2年幸免的客户在第3年被观测到。这样的选择使得只有第一年的贷款规模的影响是可识别的。
直觉上,即使贷款金额是随机的,也只会在第一年保持这种状态。之后,如果贷款金额增加违约机会,违约风险较低的客户将过多地分布在贷款金额较高的地区。它们的风险必须足够低,以抵消更高贷款金额带来的风险增加;否则,他们会在第1年违约。如果偏差太极端,甚至可能看起来更大的贷款会导致第1年之后的一年内风险下降,这是没有道理的。
解决这种选择偏差问题的一个简单方法是关注累积结果(幸免), Y ∣ t i m e > t Y|time>t Y∣time>t,而不是每年的结果(危险率), Y ∣ t i m e = t Y|time=t Y∣time=t。例如,尽管你无法确定贷款金额对第2年违约的影响, P ( D e f a u l t ∣ y r = 2 ) P(Default|yr=2) P(Default∣yr=2),但你可以轻松确定前2年金额对违约的影响, P ( D e f a u l t ∣ y r ≤ 2 ) P(Default|yr \leq 2) P(Default∣yr≤2):
g = gr.Digraph(graph_attr={"rankdir": "LR"})
g.edge("loan amount", "Default at yr=1")
g.edge("Default at yr=1", "Default at yr=2")
g.edge("Default at yr=2", "Default at yr=3")
g.edge("U", "Default at yr=1")
g.edge("U", "Default at yr=2")
g.edge("U", "Default at yr=3")
g.node("Default at yr=1", color="lightgrey", style="filled")
g.node("Default at yr=2", color="darkgrey", style="filled")
g
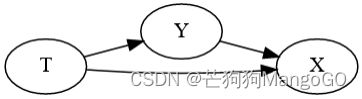
我也不想给你们一个错误的想法:仅仅控制导致选择的所有因素是一个好主意。在下面的图中,给X设置条件打开了一条非因果路径, Y → X ← T Y \rightarrow X \leftarrow T Y→X←T:
g = gr.Digraph(graph_attr={"rankdir":"LR"})
g.edge("Y", "X")
g.edge("T", "X")
g.edge("T", "Y")
g
3.8.3 给中介设置条件
虽然到目前为止所讨论的选择偏差是由于不可避免地对群体进行选择(你被迫对被调查的群体进行条件限制)而引起的,但你也可能无意中造成选择偏差。例如,假设你在人力资源部门工作,你想知道是否存在性别歧视,也就是说,资历相同的男性和女性的薪酬是否存在不同的情况。为了进行分析,你可以考虑控制资历级别;毕竟,你想要比较的是资历相同的员工,而资历似乎是一个很好的代表。换句话说,如果相同职位的男性和女性工资不同,你就有了你的公司有性别歧视的证据。
这种分析的问题在于,因果关系图可能是这样的:
g = gr.Digraph(graph_attr={"rankdir": "LR"})
g.edge("T", "M")
g.edge("T", "Y")
g.edge("M", "Y")
g.node("M", color="lightgrey", style="filled")
g.edge("woman", "seniority")
g.edge("woman", "salary")
g.edge("seniority", "salary")
g.node("seniority", color="lightgrey", style="filled")
g
资历级别是干预(性别女)和工资之间的中介。从直觉上看,男女工资差异有一个直接原因(直接路径 w o m a n → s a l a r y woman \rightarrow salary woman→salary)和一个间接原因,间接原因允许资历在该路径上流动(间接路径 w o m a n → s e n i o r i t y → s a l a r y woman \rightarrow seniority \rightarrow salary woman→seniority→salary)。这个图形告诉你的是,女性遭受歧视的一种方式是女性被提升到更高的级别的概率比较低。男女之间的薪酬差异,一方面是相同级别的薪酬差异,也有工龄差异。简单地说,这条路径 w o m a n → s e n i o r i t y → s a l a r y woman \rightarrow seniority \rightarrow salary woman→seniority→salary 也是干预和结果之间的因果路径,你不应该在分析中关闭它。如果你比较男性和女性的工资,同时控制资历,你只会发现直接的歧视, w o m a n → s a l a r y woman \rightarrow salary woman→salary。
g = gr.Digraph(graph_attr={"rankdir": "LR"})
g.edge("T", "M")
g.edge("T", "Y")
g.edge("M", "Y")
g.edge("M", "X")
g.node("X", color="lightgrey", style="filled")
g
3.9 要点总结
本章中,你主要关注因果推断的识别。我们的目标是学习如何使用图形模型来透明地了解你所做的假设,并了解这些假设需要什么样的关联(因果关系或非因果关系)。要做到这一点,你必须学习关联在图中是如何流动的。下面这张小抄是这些结构的一个很好的总结,所以建议你多加理解:
然后,你会发现识别等同于将因果关联流从图表中的非因果关联流中分离出来。你可以通过调整(设置条件限制)某些变量,甚至在图形上进行介入,关闭非因果关联路径,就像你做随机实验的情况一样。贝叶斯网络软件(如networkx)在这里特别有用,因为它可以帮助检查图中两个节点是否是连接的。例如,为了检查混杂偏差,可以简单地删除图形中的因果路径,并检查干预和结果节点是否仍然连接。如果仍然是连接的,说明有后门路径需要关闭。
最后讲了因果问题中两种很常见的偏差结构。当干预和结果具有共同的原因时,混杂偏差就会发生。这种共同原因形成了一个分叉结构,在干预和结果之间形成了一个非因果关联流:
g = gr.Digraph(graph_attr={"rankdir":"LR", "ratio": "0.3"})
g.edge("U", "T")
g.edge("U", "Y")
g.edge("T", "Y")
g
为了修正混杂偏差,你需要尝试直接或通过代理变量来调整共同原因。这激发了调整公式的想法:
A T E = ∑ x { ( E ( Y ∣ T = 1 , X = x ) − E ( Y ∣ T = 0 , X = x ) ) P ( X = x ) } ATE=\sum_x{\{(E(Y|T=1,X=x)-E(Y|T=0,X=x))P(X=x)\}} ATE=x∑{(E(Y∣T=1,X=x)−E(Y∣T=0,X=x))P(X=x)}
这也激发了条件独立性假设的想法,就是如果按照变量X分组并在组内随机化干预,那么你可以通过给X设置条件来确定因果量。
或者,如果您可以在干预节点上进行介入,混杂会变得更容易处理。例如,如果你设计一个随机实验,创建了一个新的图形,其中指向干预的箭头都被删除,这有效地消除了混杂偏差。
你还了解了选择偏差,当你对干预和结果之间的共同效果(或共同效应的子节点)进行条件限制,或者当你对中介节点(或中介节点的子节点)进行条件限制,就会出现选择偏差。选择偏差是非常危险的,因为它不会随着实验而消失。更糟糕的是,它可能非常违背直觉,很难发现:
g = gr.Digraph(graph_attr={"rankdir":"LR"})
g.edge("T", "M")
g.edge("M", "Y")
g.edge("T", "Y")
g.edge("T", "S")
g.edge("Y", "S")
g.node("M", color="lightgrey", style="filled")
g.node("S", color="lightgrey", style="filled")
g
再次强调,理解因果关系图就像学习一门新语言。通过一次又一次地查看、使用,你就可以学习掌握其大部分内容。
系列文章专栏:
使用Python进行因果推断(Causal Inference in Python)
第1章 因果推断导论
第2章 随机实验与统计学回顾
第3章 图形因果模型
持续更新中:
第4章 线性回归的不合理有效性
第5章 倾向分
第6章 效果异质性
第7章 元学习
第8章 双差分法
第9章 综合控制
第10章 Geo实验与Switchback实验
第11章 不依从性与工具
第12章 后续行动
【参考】
原版书籍《Causal Inference in Python: Applying Causal Inference in the Tech Industry》
原书github代码