【强化学习】10 —— DQN算法
文章目录
- 深度强化学习
-
- 价值和策略近似
- RL与DL结合产生的问题
- 深度强化学习的分类
- Q-learning回顾
- 深度Q网络(DQN)
-
- 经验回放
-
- 优先经验回放
- 目标网络
- 算法流程
- 代码实践
-
- CartPole环境
- 代码
- 结果
- 参考
深度强化学习
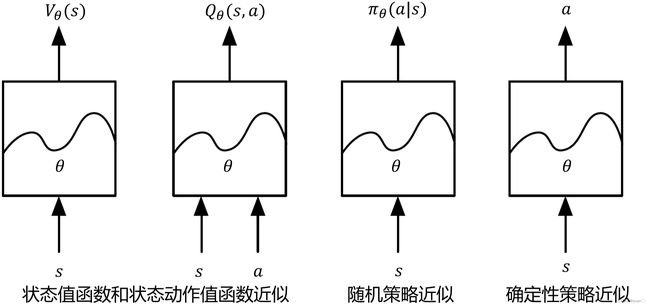
价值和策略近似
深度强化学习使强化学习算法能够以端到端的方式解决复杂问题
RL与DL结合产生的问题
• 价值函数和策略现在变成了深度神经网络
• 相当高维的参数空间
• 难以稳定地训练
• 容易过拟合
• 需要大量的数据
• 需要高性能计算
• CPU(用于收集经验数据)和GPU(用于训练神经网络)之间的平衡
深度强化学习的分类
- 基于价值的方法
• 深度Q网络及其扩展 - 基于随机策略的方法
• 使用神经网络的策略梯度,自然策略梯度,信任区域策略优化(TRPO),
近端策略优化(PPO),A3C - 基于确定性策略的方法
• 确定性策略梯度(DPG),DDPG
Q-learning回顾
文章链接——http://t.csdnimg.cn/Abz4v
Q-learning不直接更新策略,是一种基于值的方法。我们先来回顾一下 Q-learning 的更新规则 Q ( s , a ) ← Q ( s , a ) + α [ r + γ max a ′ ∈ A Q ( s ′ , a ′ ) − Q ( s , a ) ] Q(s,a)\leftarrow Q(s,a)+\alpha\left[r+\gamma\max_{a^{\prime}\in\mathcal{A}}Q(s^{\prime},a^{\prime})-Q(s,a)\right] Q(s,a)←Q(s,a)+α[r+γa′∈AmaxQ(s′,a′)−Q(s,a)]
上述公式用时序差分(temporal difference,TD)学习目标来增量式更新 r + γ max a ′ ∈ A Q ( s ′ , a ′ ) r+\gamma\max_{a'\in\mathcal A}Q(s',a') r+γmaxa′∈AQ(s′,a′),也就是说要使 Q ( s , a ) Q(s,a) Q(s,a)和 TD 目标 r + γ max a ′ ∈ A Q ( s ′ , a ′ ) r+\gamma\max_{a'\in\mathcal A}Q(s',a') r+γmaxa′∈AQ(s′,a′)靠近。于是,对于一组数据 { ( s i , a i , r i , s i ′ ) } \{(s_i,a_i,r_i,s_i')\} {(si,ai,ri,si′)},我们可以很自然地将 Q 网络的损失函数构造为均方误差的形式: ω ∗ = arg min ω 1 2 N ∑ i = 1 N [ Q ω ( s i , a i ) − ( r i + γ max a ′ Q ω ( s i ′ , a ′ ) ) ] 2 \omega^*=\arg\min_\omega\frac{1}{2N}\sum_{i=1}^N\left[Q_\omega\left(s_i,a_i\right)-\left(r_i+\gamma\max_{a'}Q_\omega\left(s_i',a'\right)\right)\right]^2 ω∗=argωmin2N1i=1∑N[Qω(si,ai)−(ri+γa′maxQω(si′,a′))]2
PS1: Q w ( s , a ) Q_w(s,a) Qw(s,a)表示Q-learning学习一个由 w w w 作为参数的函数 Q w ( s , a ) Q_w(s,a) Qw(s,a)
PS2: Q w ( s i ′ , a ′ ) Q_w(s_i',a') Qw(si′,a′)处无梯度
比较直观的想法是使用神经网络来逼近上述 Q w ( s , a ) Q_w(s,a) Qw(s,a),但是深度神经网络存在以下问题:
- 算法不稳定
- 连续采样得到的 { ( s i , a i , r i , s i ′ ) } \{(s_i,a_i,r_i,s_i')\} {(si,ai,ri,si′)}不满足独立分布。
- 会导致 Q w ( s , a ) Q_w(s,a) Qw(s,a)的频繁更新(Q-policy-data_distribution都在变)。
解决办法
- 经验回放
- 使用双网络结构:评估网络(evaluation network)和目标网络(target network)
深度Q网络(DQN)
经验回放
在一般的有监督学习中,假设训练数据是独立同分布的,我们每次训练神经网络的时候从训练数据中随机采样一个或若干个数据来进行梯度下降,随着学习的不断进行,每一个训练数据会被使用多次。在原来的 Q-learning 算法中,每一个数据只会用来更新一次 Q Q Q值。为了更好地将 Q-learning 和深度神经网络结合,DQN 算法采用了经验回放(experience replay)方法,具体做法为维护一个回放缓冲区,将每次从环境中采样得到的四元组数据(状态、动作、奖励、下一状态)存储到回放缓冲区中,训练 Q 网络的时候再从回放缓冲区中随机采样若干数据来进行训练。这么做可以起到以下两个作用。
(1)使样本满足独立假设。在 MDP 中交互采样得到的数据本身不满足独立假设,因为这一时刻的状态和上一时刻的状态有关。非独立同分布的数据对训练神经网络有很大的影响,会使神经网络拟合到最近训练的数据上。采用经验回放可以打破样本之间的相关性,让其满足独立假设。
(2)提高样本效率。每一个样本可以被使用多次,十分适合深度神经网络的梯度学习。
优先经验回放
优先经验回放可以防止数据过拟合,可以更多地关注差距较大的那些值。
Schaul, Tom, et al. “Prioritized experience replay.” arXiv preprint arXiv:1511.05952 (2015).
衡量标准
- 以 函数的值与 Target 值的差异来衡量学习的价值,即 p t = ∣ r t + γ max a ′ Q θ ( s t + 1 , a ′ ) − Q θ ( s t , a t ) ∣ p_t=|r_t+\gamma\underset{a^{\prime}}{\operatorname*{max}}Q_\theta(s_{t+1},a^{\prime})-Q_\theta(s_t,a_t)| pt=∣rt+γa′maxQθ(st+1,a′)−Qθ(st,at)∣
- 为了使各样本都有机会被采样,存储 e t = ( s t , a t , s t + 1 , r t , p t + ϵ ) e_{t}=(s_{t},a_{t},s_{t+1},r_{t},p_{t}+\epsilon) et=(st,at,st+1,rt,pt+ϵ)
- 选中的概率,样本 e t e_t et 被选中的概率为 P ( t ) = p t α ∑ k p k α P(t)=\frac{p_t^\alpha}{\sum_kp_k^\alpha} P(t)=∑kpkαptα
- 重要性采样(Importance Sampling),权重为 ω t = ( N × P ( t ) ) − β max i ω i \omega_{t}=\frac{\left(N\times P(t)\right)^{-\beta}}{\max_{i}\omega_{i}} ωt=maxiωi(N×P(t))−β
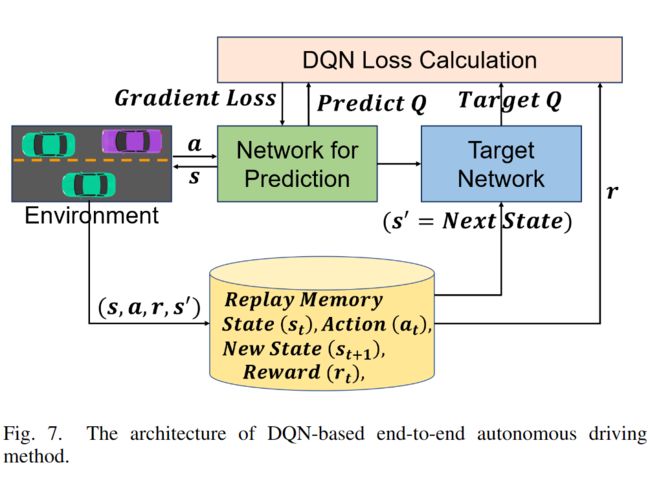
目标网络
DQN 算法最终更新的目标是让 Q w ( s , a ) Q_w(s,a) Qw(s,a)逼近 r + γ max a ′ ∈ A Q ( s ′ , a ′ ) r+\gamma\max_{a'\in\mathcal A}Q(s',a') r+γmaxa′∈AQ(s′,a′),由于 TD 误差目标本身就包含神经网络的输出,因此在更新网络参数的同时目标也在不断地改变,这非常容易造成神经网络训练的不稳定性。为了解决这一问题,DQN 便使用了目标网络(target network)的思想:既然训练过程中 Q 网络的不断更新会导致目标不断发生改变,不如暂时先将 TD 目标中的 Q 网络固定住。为了实现这一思想,我们需要利用两套 Q 网络。
(1)原来的训练网络 Q w ( s , a ) Q_w(s,a) Qw(s,a),用于计算原来的损失函数 1 2 [ Q ω ( s , a ) − ( r + γ max a ′ Q ω − ( s ′ , a ′ ) ) ] 2 \frac{1}{2}[Q_{\omega}\left(s,a\right)-\left(r+\gamma\max_{a^{\prime}}Q_{\omega^{-}}\left(s^{\prime},a^{\prime}\right)\right)]^{2} 21[Qω(s,a)−(r+γmaxa′Qω−(s′,a′))]2中的 Q w ( s , a ) Q_w(s,a) Qw(s,a)项,并且使用正常梯度下降方法来进行更新。
(2) 目标网络 Q w − ( s , a ) Q_{w^{-}}(s,a) Qw−(s,a),用于计算原先损失函数 1 2 [ Q ω ( s , a ) − ( r + γ max a ′ Q ω − ( s ′ , a ′ ) ) ] 2 \frac{1}{2}[Q_{\omega}\left(s,a\right)-\left(r+\gamma\max_{a^{\prime}}Q_{\omega^{-}}\left(s^{\prime},a^{\prime}\right)\right)]^{2} 21[Qω(s,a)−(r+γmaxa′Qω−(s′,a′))]2中的 ( r + γ max a ′ Q ω − ( s ′ , a ′ ) ) \left(r+\gamma\max_{a^{\prime}}Q_{\omega^{-}}\left(s^{\prime},a^{\prime}\right)\right) (r+γmaxa′Qω−(s′,a′))项,其中 w − w^{-} w−表示目标网络中的参数。如果两套网络的参数随时保持一致,则仍为原先不够稳定的算法。为了让更新目标更稳定,目标网络并不会每一步都更新。具体而言,目标网络使用训练网络的一套较旧的参数,训练网络 Q w ( s , a ) Q_w(s,a) Qw(s,a)在训练中的每一步都会更新,而目标网络 Q w − ( s , a ) Q_{w^{-}}(s,a) Qw−(s,a)的参数每隔 C C C步才会与训练网络同步一次,即 w − ← w w^{-}\leftarrow w w−←w。这样做使得目标网络相对于训练网络更加稳定。
算法流程
代码实践
CartPole环境
Cart Pole gymnasium文档
pytorch官方教程REINFORCEMENT LEARNING (DQN) TUTORIAL
(使用stable_baselines3)强化学习训练的模型怎么存储?比如OpenAI-gym训练好的模型? -
https://www.zhihu.com/question/67825049/answer/2794069082

在车杆环境中,有一辆小车,智能体的任务是通过左右移动保持车上的杆竖直,若杆的倾斜度数过大,或者车子离初始位置左右的偏离程度过大,或者坚持时间到达 500 帧,则游戏结束。智能体的状态是一个维数为 4 的向量,每一维都是连续的,其动作是离散的,动作空间大小为 2。在游戏中每坚持一帧,智能体能获得分数为 1 的奖励,坚持时间越长,则最后的分数越高,坚持 500 帧即可获得最高的分数。
状态空间Box([-4.8000002e+00 -3.4028235e+38 -4.1887903e-01 -3.4028235e+38], [4.8000002e+00 3.4028235e+38 4.1887903e-01 3.4028235e+38], (4,), float32)
| 维度 | 意义 | 最小值 | 最大值 |
|---|---|---|---|
| 0 | 车的位置 | -2.4 | 2.4 |
| 1 | 车的速度 | -Inf | Inf |
| 2 | 杆的角度 | ~ -41.8° | ~ 41.8° |
| 3 | 杆尖端的速度 | -Inf | Inf |
动作空间Discrete(2)
| 标号 | 动作 |
|---|---|
| 0 | 向左移动小车 |
| 1 | 向右移动小车 |
代码
import random
import gymnasium as gym
import numpy as np
import collections
from tqdm import tqdm
import torch
import torch.nn.functional as F
import util
class ReplayBuffer:
''' 经验回放池 '''
def __init__(self, capacity):
self.buffer = collections.deque(maxlen=capacity) # 队列,先进先出
# 将数据加入buffer
def add(self, state, action, reward, next_state, terminated, truncated):
self.buffer.append((state, action, reward, next_state, terminated, truncated))
# 从buffer中采样数据,数量为batch_size
def sample(self, batch_size):
transitions = random.sample(self.buffer, batch_size)
state, action, reward, next_state, terminated, truncated = zip(*transitions)
return np.array(state), action, reward, np.array(next_state), terminated, truncated
# 目前buffer中数据的数量
def size(self):
return len(self.buffer)
class Qnet1(torch.nn.Module):
''' 只有一层隐藏层的Q网络 '''
def __init__(self, state_dim, hidden_dim, action_dim):
super(Qnet1, self).__init__()
self.fc = torch.nn.Sequential(
torch.nn.Linear(state_dim, hidden_dim),
torch.nn.ReLU(),
torch.nn.Linear(hidden_dim, action_dim)
)
def forward(self, x):
return self.fc(x)
class DQN:
''' DQN算法 '''
def __init__(self, state_dim, hidden_dim, action_dim, learning_rate, gamma,
epsilon, target_update_rate, device, numOfEpisodes, env,
buffer_size, minimal_size, batch_size):
self.action_dim = action_dim
# Q网络
self.q_net = Qnet1(state_dim, hidden_dim, self.action_dim).to(device)
# 目标网络
self.target_q_net = Qnet1(state_dim, hidden_dim, self.action_dim).to(device)
# 使用Adam优化器
self.optimizer = torch.optim.Adam(self.q_net.parameters(),
lr=learning_rate)
self.gamma = gamma
self.epsilon = epsilon
# 目标网络更新频率
self.target_update_rate = target_update_rate
# 计数器,记录更新次数
self.count = 0
self.device = device
self.numOfEpisodes = numOfEpisodes
self.env = env
self.buffer_size = buffer_size
self.minimal_size = minimal_size
self.batch_size = batch_size
# Choose A from S using policy derived from Q (e.g., epsilon-greedy)
def ChooseAction(self, state):
if np.random.random() < self.epsilon:
action = np.random.randint(self.action_dim)
else:
state = torch.tensor(np.array([state]), dtype=torch.float).to(self.device)
action = self.q_net(state).argmax().item()
return action
def Update(self, transition_dict):
states = torch.tensor(transition_dict['states'],
dtype=torch.float).to(self.device)
actions = torch.tensor(transition_dict['actions']).view(-1, 1).to(self.device)
rewards = torch.tensor(transition_dict['rewards'],
dtype=torch.float).view(-1, 1).to(self.device)
next_states = torch.tensor(transition_dict['next_states'],
dtype=torch.float).to(self.device)
terminateds = torch.tensor(transition_dict['terminateds'],
dtype=torch.float).view(-1, 1).to(self.device)
truncateds = torch.tensor(transition_dict['truncateds'],
dtype=torch.float).view(-1, 1).to(self.device)
#Q值?
q_values = self.q_net(states).gather(1, actions)
# 下个状态的最大Q值
max_next_q_values = self.target_q_net(next_states).max(1)[0].view(-1, 1)
# TD误差目标
q_targets = rewards + self.gamma * max_next_q_values * (1 - terminateds + truncateds)
# 均方误差损失函数
dqn_loss = torch.mean(F.mse_loss(q_values, q_targets))
# PyTorch中默认梯度会累积,这里需要显式将梯度置为0
self.optimizer.zero_grad()
# 反向传播更新参数
dqn_loss.backward()
self.optimizer.step()
if self.count % self.target_update_rate == 0:
self.target_q_net.load_state_dict(
self.q_net.state_dict()) # 更新目标网络
self.count += 1
def DQNtrain(self):
replay_buffer = ReplayBuffer(self.buffer_size)
returnList = []
for i in range(10):
with tqdm(total=int(self.numOfEpisodes / 10), desc='Iteration %d' % i) as pbar:
for episode in range(int(self.numOfEpisodes / 10)):
# initialize state
state, info = self.env.reset()
terminated = False
truncated = False
episodeReward = 0
# Loop for each step of episode:
while (not terminated) or (not truncated):
action = self.ChooseAction(state)
next_state, reward, terminated, truncated, info = self.env.step(action)
replay_buffer.add(state, action, reward, next_state, terminated, truncated)
if terminated or truncated:
break
state = next_state
episodeReward += reward
# 当buffer数据的数量超过一定值后,才进行Q网络训练
if replay_buffer.size() > self.minimal_size:
b_s, b_a, b_r, b_ns, b_te, b_tr = replay_buffer.sample(self.batch_size)
transition_dict = {
'states': b_s,
'actions': b_a,
'next_states': b_ns,
'rewards': b_r,
'terminateds': b_te,
'truncateds': b_tr
}
self.Update(transition_dict)
returnList.append(episodeReward)
if (episode + 1) % 10 == 0: # 每10条序列打印一下这10条序列的平均回报
pbar.set_postfix({
'episode':
'%d' % (self.numOfEpisodes / 10 * i + episode + 1),
'return':
'%.3f' % np.mean(returnList[-10:])
})
pbar.update(1)
return returnList
def test01():
device = torch.device("cuda") if torch.cuda.is_available() else torch.device("cpu")
env = gym.make("CartPole-v1", render_mode="human")
# random.seed(0)
# np.random.seed(0)
# torch.manual_seed(0)
returnLists1 = []
ReturnList = []
agent = DQN(state_dim=env.observation_space.shape[0],
hidden_dim=128,
action_dim=2,
learning_rate=2e-3,
gamma=0.98,
epsilon=0.01,
target_update_rate=10,
device=device,
numOfEpisodes=500,
env=env,
buffer_size=10000,
minimal_size=500,
batch_size=64)
returnLists1.append(agent.DQNtrain())
ReturnList.append(util.smooth(returnLists1, sm=100))
labelList = ['DQN']
util.PlotReward(500, ReturnList, labelList, 'CartPole-v1')
np.save("D:\LearningRL\Hands-on-RL\DQN_CartPole\ReturnData\DQN_CartPole_v0_2.npy", returnLists1)
env.close()
if __name__ == "__main__":
test01()
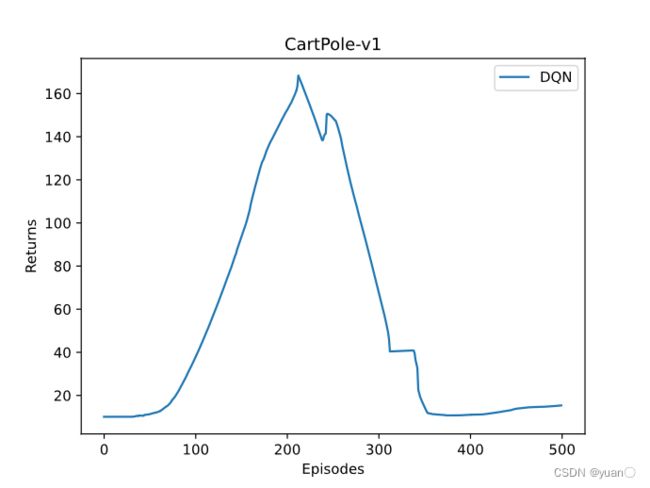
结果
一次比较“好”的结果
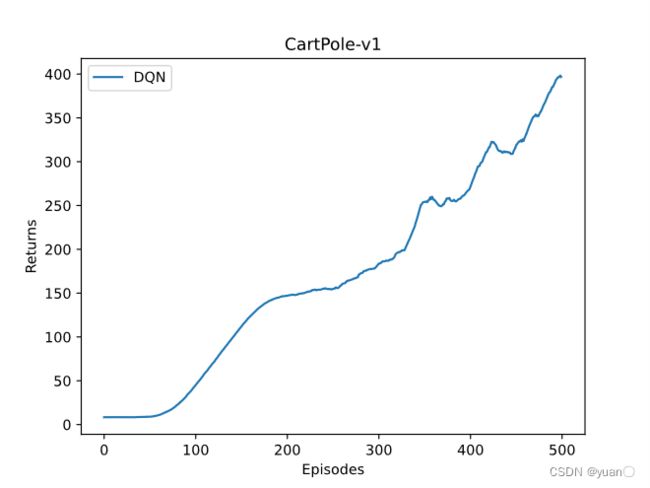
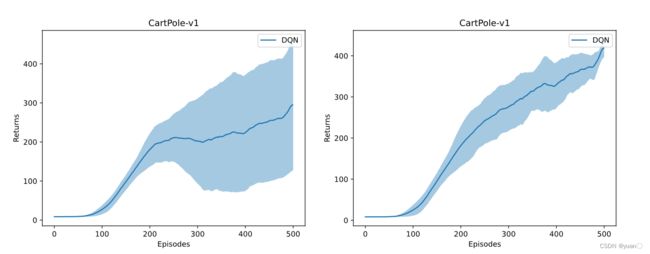
左(保留训练效果不理想),右(剔除训练效果不理想)
参考
[1] 伯禹AI
[2] https://www.davidsilver.uk/teaching/
[3] 动手学强化学习
[4] Reinforcement Learning