LSTM长短期记忆网络,GRU
目录
- 前言
- 一. LSTM
-
- 1.1. 设计思路
- 1.2. 前向传播
- 1.3. LSTM原理
-
- 1.3.1. 记忆细胞
- 1.4. LSTM为什么能缓解梯度消失
- 二. GRU
-
- 2.1. 结构和原理
- 1.3. LSTM和GRU的区别
前言
上一篇博文我们介绍了RNN循环神经网络,虽然神经网络在解决时序问题是有着不错的表现,但是也有一个非常严重的问题,就是当网络结构比较深的时候,RNN网络由于前后的关联性导致了其在反向传播的时候会出现梯度消失或者梯度爆炸的情况,导致其很难实现真正落地。于是引出了我们今天要介绍的长短期记忆模型LSTM。
一. LSTM
1.1. 设计思路
RNN
RNN的设计思路是把所有的信息都记住,不管是有用的还是没用的信息。
LSTM
设计一个记忆细胞,具有选择性记忆的功能,可以选择记忆重要的信息,过滤掉噪声,减轻记忆负担
1.2. 前向传播
先来看下整体的网络结构:
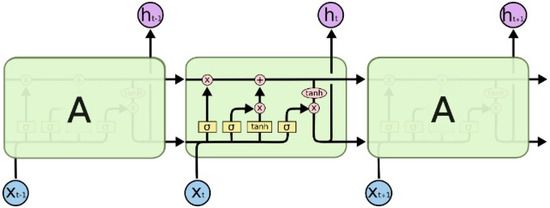
乍一看LSTM很唬人,其实就是一个纸老虎,我们来拆分他的结构看一下。先跟RNN的网络结构对比一下看看区别是什么,下面是RNN的网络结构:
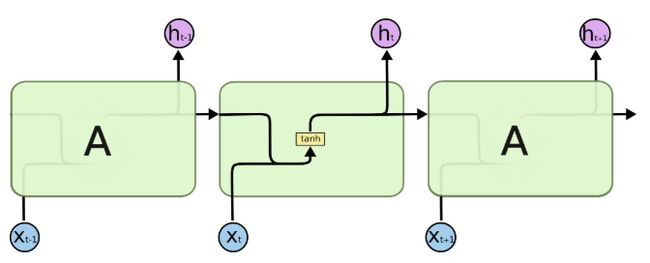
RNN和LSTM的区别:
- LSTM内部多了很多的操作
- RNN是一个箭头,LSTM是两个箭头,LSTM的上面一部分的箭头就是我们说的记忆细胞。
我们来详细看下LSTM的其中一部分的内部结构,如下图所示:
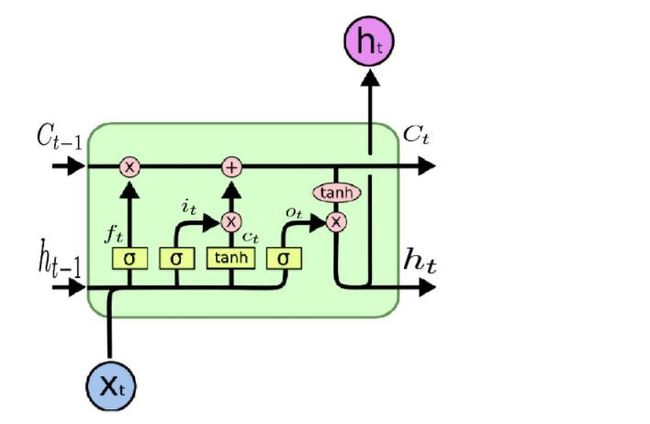
图示说明:
- 上面的 C t − 1 C_{t-1} Ct−1和 C t C_t Ct就是记忆细胞的部分,表示cell
- h t h_t ht表示的是状态
- σ \sigma σ表示门单元,输出介于0-1之间,其中 f t f_t ft表示遗忘门forget, i t i_t it表示更新门, o t o_t ot表示输出门
我们把上面的内部结构的公式写出来如下,上面有一个门单元 c t c_t ct与C_t容易引起歧义,下面我们用 g t g_t gt代替:
{ i t = σ ( i ~ t ) = σ ( W x i x t + W h i h t − 1 + b i ) f t = σ ( f ~ t ) = σ ( W x f x t + W h f h t − 1 + b f ) g t = tanh ( g ~ t ) = tanh ( W x g x t + W h g h t − 1 + b g ) o t = σ ( o ~ t ) = σ ( W x o x t + W h o h t − 1 + b o ) c t = c t − 1 ⊙ f t + g t ⊙ i t m t = tanh ( c t ) h t = o t ⊙ m t y t = W y h h t + b y \left\{\begin{array}{l} i_t=\sigma\left(\tilde{i}_t\right)=\sigma\left(W_{x i} x_t+W_{h i} h_{t-1}+b_i\right) \\ f_t=\sigma\left(\tilde{f}_t\right)=\sigma\left(W_{x f} x_t+W_{h f} h_{t-1}+b_f\right) \\ g_t=\tanh \left(\tilde{g}_t\right)=\tanh \left(W_{x g} x_t+W_{h g} h_{t-1}+b_g\right) \\ o_t=\sigma\left(\tilde{o}_t\right)=\sigma\left(W_{x o} x_t+W_{h o} h_{t-1}+b_o\right) \\ c_t=c_{t-1} \odot f_t+g_t \odot i_t \\ m_t=\tanh \left(c_t\right) \\ h_t=o_t \odot m_t \\ y_t=W_{y h} h_t+b_y \end{array}\right. ⎩ ⎨ ⎧it=σ(i~t)=σ(Wxixt+Whiht−1+bi)ft=σ(f~t)=σ(Wxfxt+Whfht−1+bf)gt=tanh(g~t)=tanh(Wxgxt+Whght−1+bg)ot=σ(o~t)=σ(Wxoxt+Whoht−1+bo)ct=ct−1⊙ft+gt⊙itmt=tanh(ct)ht=ot⊙mtyt=Wyhht+by
1.3. LSTM原理
上面我们列出了LSTM的计算过程 ,看起来很复杂,下面我们来看下他LSTM里面的各个单元所起到的作用是什么。
1.3.1. 记忆细胞
在LSTM的每个的每个时间步里面,都有一记忆cell,这个东西给予了LSTM记忆功能,使得LSTM有能力自由的选取每个时间步里面的记忆内容。简言之就是自己选择记住或者忘记。
举个栗子来解释,还是以下图为例:

场景:考试周,每个时间考一门试。
假设我们当前时间应该考概率论这门课,那么在此时 X t X_t Xt时刻,我们应该复习的就是概率论这门课。这个结构的内部的一些操作就是复习过程中形成的记忆,在复习的过程中会生成新的记忆,然后带着这些记忆去参加考试, h t h_t ht就是考完概率论的得分。那么前面的 C t − 1 C_{t-1} Ct−1就是上一门考试的记忆,假设是高数,那么 h t − 1 h_{t-1} ht−1就是考完高数的状态的结果。简言之, h t h_t ht是当前状态的结果, C t C_t Ct是当前状态历史记忆的缓存。这里会有一个假设,假设我们的脑容量是有限的,意思就是考完高数之后就尽可能的把脑子里面的跟下一门考试概率论没有关系的记忆给抹除掉,腾出位置来给概率论做记忆的准备,这个就是遗忘门 f t f_t ft要干的事情, f t f_t ft里面很多介于0-1之间的值,比如说高数里面微积分对概率论有用,那么就保留,像空间向量这些对概率论没用的就抹除掉。那么更新门是干嘛用的呢? g t g_t gt(图中给的是 c t c_t ct,为了避免引起歧义,这里用 g t g_t gt)是我们看完概率论之后学习到的内容,但是里面有很多跟考点不想干,所以引入了更新门 i t i_t it来更新学习到的内容。最终形成新的记忆 C t C_t Ct, C t C_t Ct有保留的上一次的状态+这次新学到的状态,可以理解为微积分能力+新学到的概率论的知识,然后去参加考试。
有没有发现上面有一个门我们一直没介绍,就是输出门 o t o_t ot,输出门是什么,为什么最后又加了一个输出么,作用是什么?同样结合上面的考试的例子来解释,考点很多,我们复习到的东西有很多,但是考试的时候就考那几题,所以 o t o_t ot就是让我只需要用我复习到的一部分的知识就行了。
总结:
- 遗忘门决定我要忘记哪些
- 更新门决定我要记住哪些新知识
- 输出门决定我要根据需要输出哪些
1.4. LSTM为什么能缓解梯度消失
在了解了LSTM的原理之后,我们来看下为什么LSTM能够缓解梯度消失的问题?
回顾一下RNN梯度消失的原因:
权重的连乘导致梯度消失或者梯度爆炸,罪魁祸首就是连乘项的权重。
下面我们来看一下为什么LSTM能够缓解梯度消失,看下下面的推到图,看着非常负复杂,有很多的参数,有点劝退,下面我们来注意剖析解开它神秘的面纱。
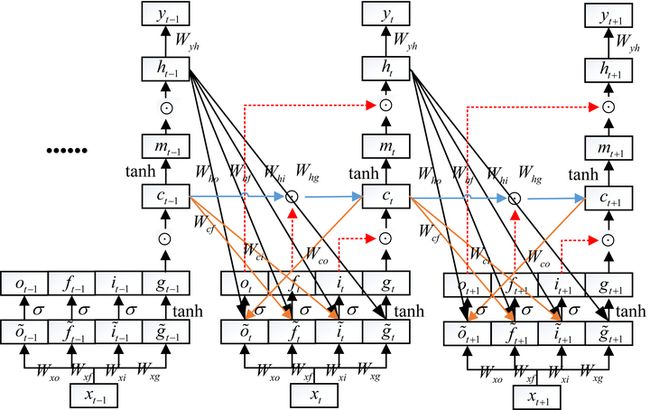
以图中的三个节点为例,最后一个是t=3,最前面是t=1,以推到 w x f w_{xf} wxf为例进行推导:
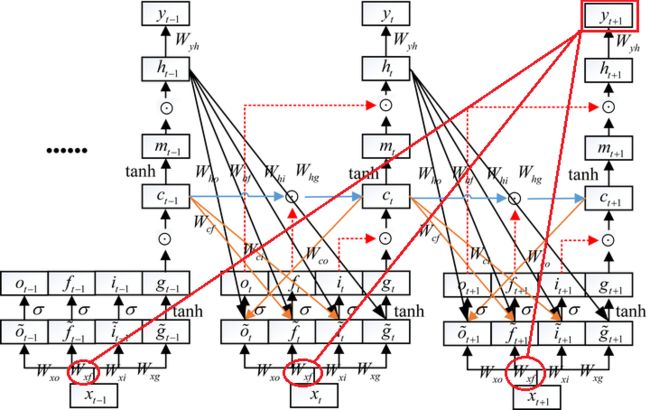
总共要对以上三个节点都求解导,记住核心就是复合函数的链式求导法则,涉及路线和变量过于复杂,这里就不推导了,直接贴一个哔站大佬的推导结果:LSTM反向传播推导。

由于推到过程过于繁琐复杂,对第一个节点的推导直接用路线表示:
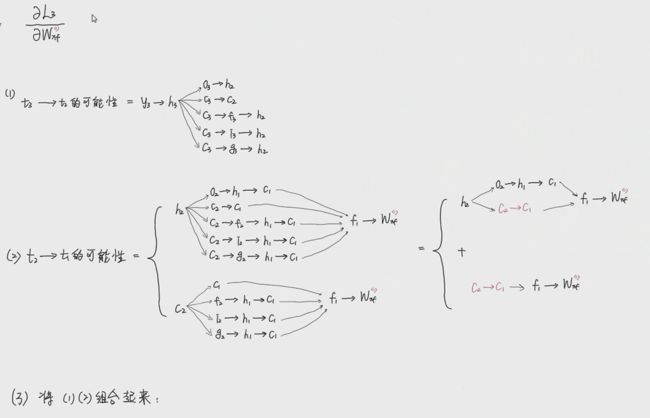
最终化简成下面的式子:
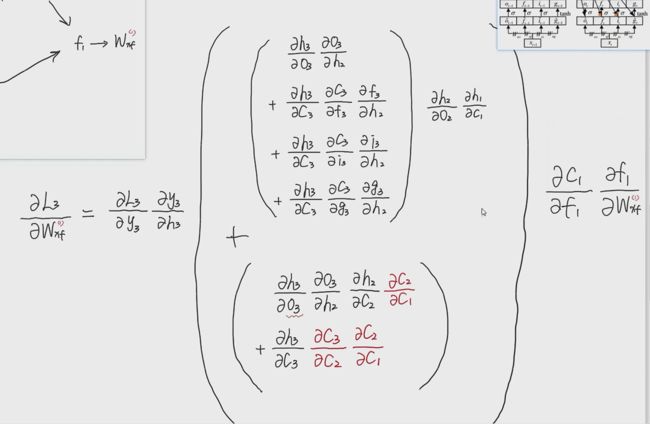
对红色的部分求解,可以对着前向传播的公式求解:
{ i t = σ ( i ~ t ) = σ ( W x i x t + W h i h t − 1 + b i ) f t = σ ( f ~ t ) = σ ( W x f x t + W h f h t − 1 + b f ) g t = tanh ( g ~ t ) = tanh ( W x g x t + W h g h t − 1 + b g ) o t = σ ( o ~ t ) = σ ( W x o x t + W h o h t − 1 + b o ) c t = c t − 1 ⊙ f t + g t ⊙ i t m t = tanh ( c t ) h t = o t ⊙ m t y t = W y h h t + b y \left\{\begin{array}{l} i_t=\sigma\left(\tilde{i}_t\right)=\sigma\left(W_{x i} x_t+W_{h i} h_{t-1}+b_i\right) \\ f_t=\sigma\left(\tilde{f}_t\right)=\sigma\left(W_{x f} x_t+W_{h f} h_{t-1}+b_f\right) \\ g_t=\tanh \left(\tilde{g}_t\right)=\tanh \left(W_{x g} x_t+W_{h g} h_{t-1}+b_g\right) \\ o_t=\sigma\left(\tilde{o}_t\right)=\sigma\left(W_{x o} x_t+W_{h o} h_{t-1}+b_o\right) \\ c_t=c_{t-1} \odot f_t+g_t \odot i_t \\ m_t=\tanh \left(c_t\right) \\ h_t=o_t \odot m_t \\ y_t=W_{y h} h_t+b_y \end{array}\right. ⎩ ⎨ ⎧it=σ(i~t)=σ(Wxixt+Whiht−1+bi)ft=σ(f~t)=σ(Wxfxt+Whfht−1+bf)gt=tanh(g~t)=tanh(Wxgxt+Whght−1+bg)ot=σ(o~t)=σ(Wxoxt+Whoht−1+bo)ct=ct−1⊙ft+gt⊙itmt=tanh(ct)ht=ot⊙mtyt=Wyhht+by
可以看出模型可以通过学习区控制权重系数的大小来控制 ∂ C t ∂ C t − 1 \frac{\partial C_t}{\partial C_{t-1}} ∂Ct−1∂Ct让其接近于1,从而缓解梯度消失和梯度爆炸的现象。
二. GRU
上面经过梯度的反向传播的推导可以看出,LSTM可以缓解梯度消失和梯度爆炸的情况,但是他的参数量太多了,计算很复杂,训练的复杂度也变得很高,模型很容易出现过拟合。于是出现了LSTM的轻量版本GRU。我们下面来简单介绍下。
2.1. 结构和原理
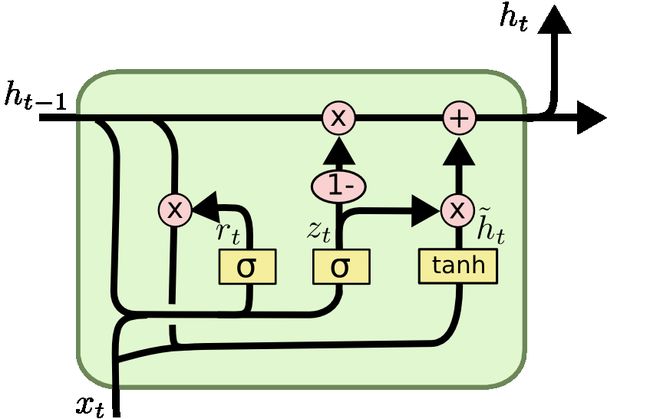
其中:
z t = σ ( W z ⋅ [ h t − 1 , x t ] ) r t = σ ( W r ⋅ [ h t − 1 , x t ] ) h ~ t = tanh ( W ⋅ [ r t ∗ h t − 1 , x t ] ) h t = ( 1 − z t ) ∗ h t − 1 + z t ∗ h ~ t \begin{aligned} z_t & =\sigma\left(W_z \cdot\left[h_{t-1}, x_t\right]\right) \\ r_t & =\sigma\left(W_r \cdot\left[h_{t-1}, x_t\right]\right) \\ \tilde{h}_t & =\tanh \left(W \cdot\left[r_t * h_{t-1}, x_t\right]\right) \\ h_t & =\left(1-z_t\right) * h_{t-1}+z_t * \tilde{h}_t \end{aligned} ztrth~tht=σ(Wz⋅[ht−1,xt])=σ(Wr⋅[ht−1,xt])=tanh(W⋅[rt∗ht−1,xt])=(1−zt)∗ht−1+zt∗h~t
对比下LSTM的结构,可以发现,GRU的门少了,并且GRU只有左边的一项输入,LSTM有两项,在GRU中可以认为 h t h_{t} ht是将 C t C_t Ct和 h t h_t ht合二为一了。LSTM里面是遗忘门,更新门,输出门,GRU里面变为了更新门和重置门,对应到图里面就是 r t r_t rt和 z t z_t zt。核心的思路就是 h t = ( 1 − z t ) ∗ h t − 1 + z t ∗ h ~ t h_t =\left(1-z_t\right) * h_{t-1}+z_t * \tilde{h}_t ht=(1−zt)∗ht−1+zt∗h~t, h t − 1 h_{t-1} ht−1是前一时刻的内容,通过 1 − z t 1-z_t 1−zt进行选择记忆哪些东西,遗忘掉哪些东西, h ~ t \tilde{h}_t h~t是当下所形成的新的内容,通过 z t z_t zt进行选择要记住哪些东西,过滤掉哪些东西。
同样我们举一个例子来解释GRU:以大学所修的学学科为例,如高数,线代,概率论,数电,模电,电路,C语言等,对这些学科我们都整理出了一部分的笔记代表这些学科的重点内容,那么:
h t − 1 = [ 高数,线代,概率论,数电,模电,电路, C 语言 ] x t = 机器学习 h t = [ 高数,线代,概率论, S V M ,决策树, P y t h o n ] h_{t-1}= [高数,线代,概率论,数电,模电,电路,C语言] \ \\ x_t =机器学习 \ \\ h_t= [高数,线代,概率论,SVM,决策树,Python] ht−1=[高数,线代,概率论,数电,模电,电路,C语言] xt=机器学习 ht=[高数,线代,概率论,SVM,决策树,Python]
我们将我们的笔记都放在了书柜里面,假设我们现在要学习机器学习这门课,我们现在要做的事情就是从以往的这些笔记中选取跟机器学习有关的笔记,挑选出来进行一波学习,但是我们的书柜容量是有限的,当我们学完之后我们需要把那些跟机器学习没关系的笔记给扔掉,然后把机器学习里面学习到的新的内容给它存进去,比如SVM,python等。下面我们来看下这些门做了些什么事情:
首先是重置门 r t r_t rt,他做了什么事情呢,首先就是从书柜中筛选出跟机器学习有关的笔记,比如通过这个sigmoid函数计算之后得出如下的向量,表示笔记对学习机器学习的帮助:
r t = [ 0.5 , 0.6.0.7 , 0.01 , 0.02 , 0.01 , 0.2 ] r_t = [0.5, 0.6. 0.7, 0.01, 0.02, 0.01, 0.2] rt=[0.5,0.6.0.7,0.01,0.02,0.01,0.2]
可以看出重置门就是一个求取相关系数的门,求得的结果是一个百分比。下面就将求得的结果应用于笔记,从中提取相关的内容,对应的就是 h ~ t \tilde{h}_t h~t中的 r t ∗ h t − 1 r_t*h_{t-1} rt∗ht−1的部分,可以理解成从这些学科里面吧跟机器学习相关的内容给提取出来了,要用提取出来的这部分的知识区阅读机器学习这个书本,前面的激活函数 t a n h tanh tanh就相当于学习的过程,整理出一份关于机器学习得我笔记。假设我们整理出来的新笔记如下:
h ~ t = [ 出版社,矩阵分解,极大似然估计线性回归, S V M ,决策树, P y t h o n 语言 ] \tilde{h}_t = [出版社,矩阵分解,极大似然估计线性回归,SVM,决策树,Python语言 ] h~t=[出版社,矩阵分解,极大似然估计线性回归,SVM,决策树,Python语言]
可以看出里面会有一些跟我们学机器学习没关系的信息,比如出版社。以及一些冗余项,如矩阵分解在线性代数里面已经学过了,极大似然估计是概率论里面的。重复的内容吗,如python语言。我不需要再重复的把这些相似的这个笔记给存放进去,不相关的也不能放进书柜里面。所以就有了:
z t = σ ( W z ⋅ [ h t − 1 , x t ] ) z_t =\sigma\left(W_z \cdot\left[h_{t-1}, x_t\right]\right) zt=σ(Wz⋅[ht−1,xt])
从上面的前向传播可以看出,他的作用只有两个地方, h t − 1 h_{t-1} ht−1和 h t h_t ht, z t ∗ h ~ t z_t * \tilde{h}_t zt∗h~t可以理解成当前整理的笔记,把重复的,没用的部分抹除,有用的保留下来, ( 1 − z t ) ∗ h t − 1 (1-z_t )* h_{t-1} (1−zt)∗ht−1可以理解成把没用的笔记清理掉,有用的保留下来,最终就得到了我们下面的公式:
h t = ( 1 − z t ) ∗ h t − 1 + z t ∗ h ~ t h_t =\left(1-z_t\right) * h_{t-1}+z_t * \tilde{h}_t ht=(1−zt)∗ht−1+zt∗h~t
h t h_t ht就是我们学习的机器学习的笔记。
1.3. LSTM和GRU的区别
- 事实上,这两种模型在许多任务中都不相上下,因此,与挑选出一个理想的架构相比,调整层数这些超参数等更重要;
- GRU的参数较少,因此其训练速度更快,或需要归纳的数据更少。相对应的,如果有足够的训练数据,表达能力更强的LSTM或许效果更佳;
- 相比较于LSTM,GRU能降低过拟合风险;
- GRU能够缓解梯度消失(可参考LSTM的推导,GRU只是LSTM的轻量版本,没有实质性差别)
问:为什么LSTM和GRU都能缓解梯度消失呢,从结构上解释。
答:核心就是因为这些门的设计,赋予了模型的一种选择记忆的功能,可以自由选择参数是否更新。
补充:
以上的不管是LSTM还是GRU举的例子,都只是为了便于理解,实际在炼丹的时候,模型的参数都是自己学的,能不能学到有用的信息要看网络怎么设计的,输入数据,超参数等各种因素。