数据结构---交换排序
交换排序:借助于“交换”的排序
最开始:49 38 65 97 76 13 27 49
我们追求的是递增的序列

第一趟结束之后会将最小的元素 13 冒 到最前面
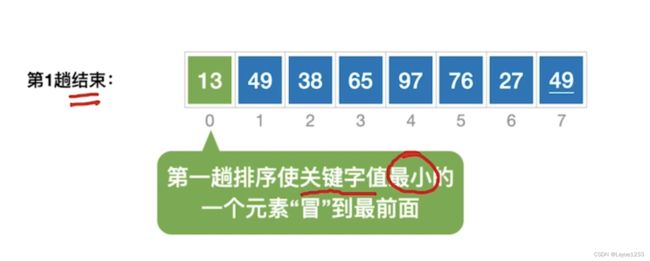
再进行第二趟的时候:
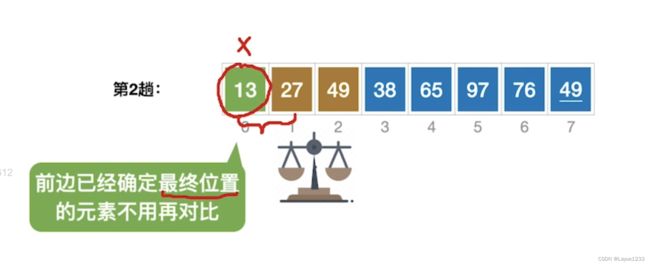
第二小的元素27,不需要再和13进行比较!
因为经过之前的那一趟的处理之后,13这个元素的最终位置已经确定了,不可能再改变,它是最小的元素。
第二趟的结果是把最小的两个到了前面两个
第三趟: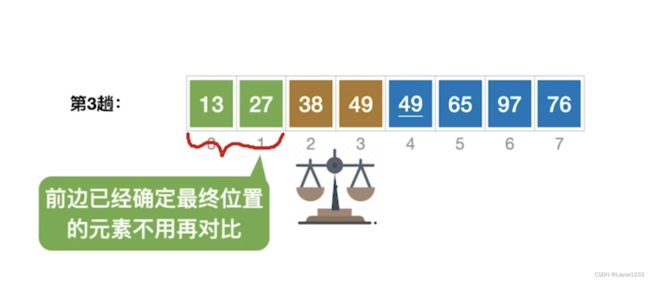
将38冒到第三位置的时候,同样的,前面已经确定了的元素,我们不需要再往前对比。第三趟我们对比到2 和 3 就已经行了。
第四趟
如果遇到两个相同的值的时候,不应该交换俩位置,这么做可以保证算法的稳定性,原本在右边的元素不会跑到左边去。

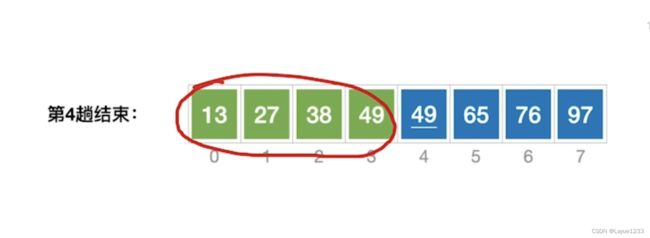
第四趟结束如上图,前面四个元素位置已经确定了。
第五趟排序:
76与97不需要交换 65与76不需要交换 49与65不需要交换 49与49也不需要交换
最终为:
实际上第五趟排序没有发生交换,我们就可以确定其实整个表已经有序了。我们就不需要再进行第六趟的排序。

在理解了上方之后,算法如下:
1.定义了一个交换操作:

2.

if语句所做的事情是判断j所指向的元素和它前面的这个元素,它们的大小关系,如果是逆序的话,那么就会调用我们之前定义的交换函数。
一旦发生交换,我们就把flag的标记位设置为true

因为我们之前说过,一趟冒泡排序过程当中如果没有发生任何一次交换,那么其实我们就可以提前让这个算法结束。

最后if语句就是提前结束算法。(上面就是flag变量的作用)
j变量的作用
j变量会将当前还没有排好序的这些序列全部两两检查一遍。
值得注意的是:
只有A[j-1]>A[j]的时候,才交换,也就是说左右两边的值相等的时候,是不会交换的,那么这么做是可以保证算法是稳定的。

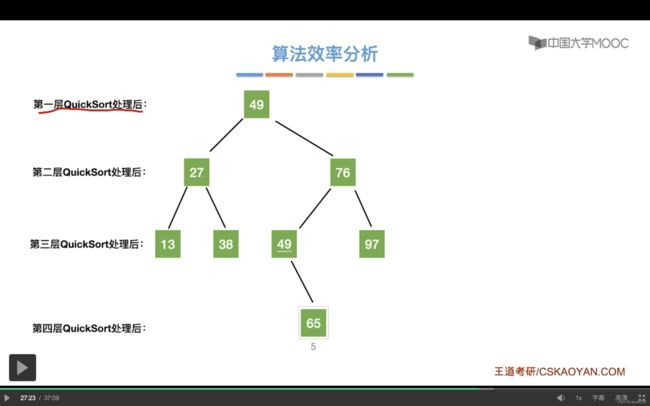
算法效率分析:
空间复杂度:算法只使用了几个辅助变量,因此是常数级别的。
时间复杂度:最好情况是,有序的情况:

根据我们之前说的,这一趟没有发生交换,那么这个算法就会直接停止。因此总共只需要一趟排序,并且这趟排序只需要进行对比元素就行,一共对比n-1次,而且所有的元素都不需要交换。
最坏的情况:原本就是逆序的,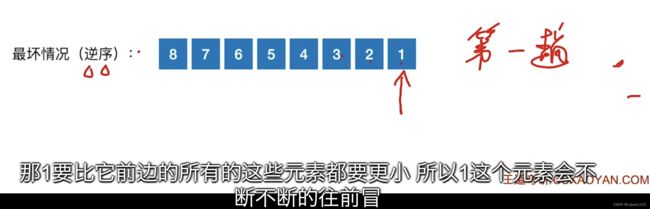
每次一次对比都会导致一次交换。因此交换次数和比较次数都是一样的。
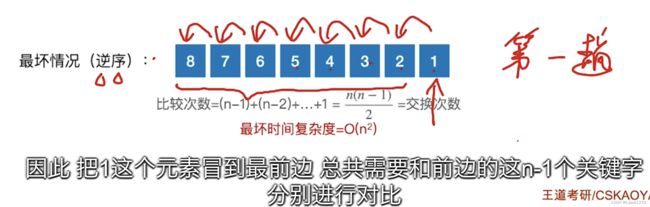
冒泡排序的平均时间复杂度也会达到n方这样一个数量级。
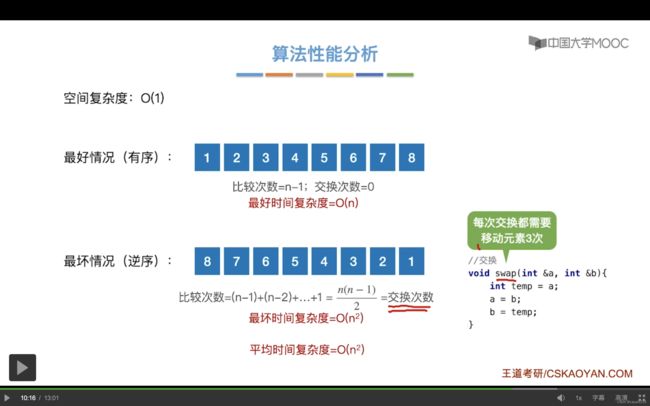
另外,交换次数是调用swap函数的次数,每次交换都需要交换3次。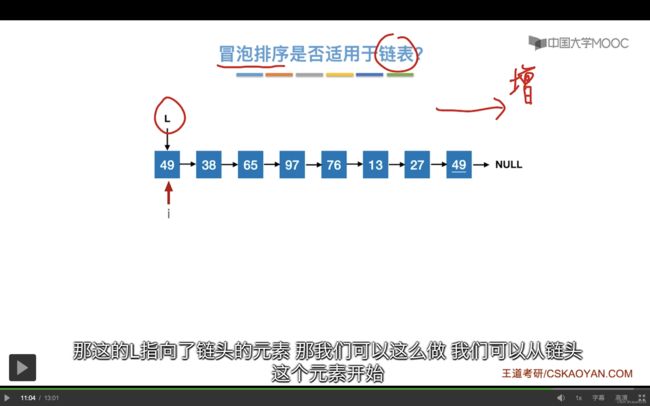
冒泡排序适用于链表,我们从链头这个元素开始,依次扫描,实现链表递增。
让i和i后面的元素进行比较,只要是逆序,就交换。
总之,冒泡排序思想的实现是适用于链表的。
小结:
冒泡排序注意一点是:如果某一趟排序过程中没有发生“交换”,则算法是可以提前结束的。
快速排序
算法:
首先,Partition函数用于划分,压入栈顶,包括low high变量的值0和7,实际上96应该是交给partition函数进行保存的。
然后进入Partition函数:第一句我们会让low指针所指向的这个元素,用一个叫做pivot的变量把它保存下来。

当前这个while循环我们想要做的事情就是让high指针不断左移,直到找一个比枢轴元素更小的元素为止,才会跳出这个while循环。然后把high所指的元素放到low所指的这个位置。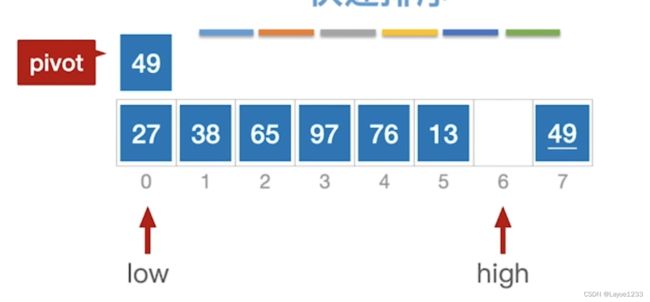
继续往后,又有一个while循环,
low指针会不断的右移,直到找到一个比49更大的元素为止,才会跳出while循环。low指向65。然后把low指向的元素放到high所指向的位置: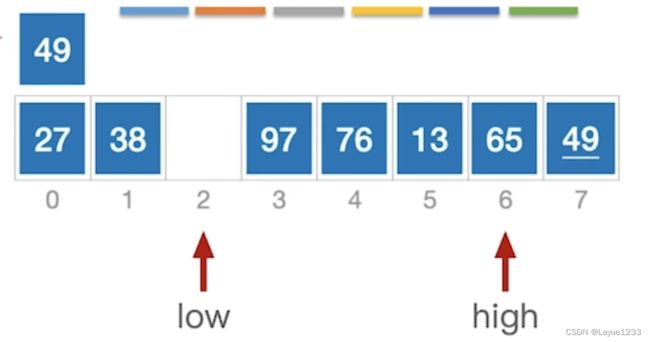
**接下来,由于low同样还是小于high,我们会让大循环继续运行下去。**然后又到了这个小循环,还记得这个小循环做的事情吗,我们会让high指针不断的左移,直到找到一个比high更小的元素为止(13)(当前high所指的元素因不满足A[high]>=pivot而跳出循环)。接下来,又让low指针右移,找到一个比49更大的元素,把它放到high指针所指的位置。。。。。。
所以,直到high一直左移,移到和low相等的位置,才会因为:
low
因此,接下来这句的处理相当于什么也没做。
然后又到下一个小循环,此时由于不满足low小于high,那么low指针也不会继续向右移动了。
同样的,再到了上面这一句了,high和low指向的是同一个位置,那么接下来这个代码相当于什么也没做。
而此时,再回到当前的while大循环,由于low与high的值相等,不满足,可以跳出这个循环。

跳出大循环,执行下一句,也就是将我们之前保存的pivot变量赋予low指向的位置,也就是下图:
这样就完成了一次划分,不难证明pivot右边全是比pivot大的元素,pivot左边全是比pivot小的元素。(等号都不行)
这样执行完Partition函数之后,return low的值。递归工作栈的栈顶将会弹出Partition函数,因此栈顶是QS函数。也就是如下图所示,并且我们也通过一次划分,确定了以3这个位置为基准划分成了左右两个部分,。
函数执行QS函数调用,进入QS之后再调用Paritition函数。这两次调用之后的系统工作栈如下图所示:
因此Partition函数进入之后,low的值是0,high的值为3-1=2,Partition函数的功能是划分,执行完之后,为: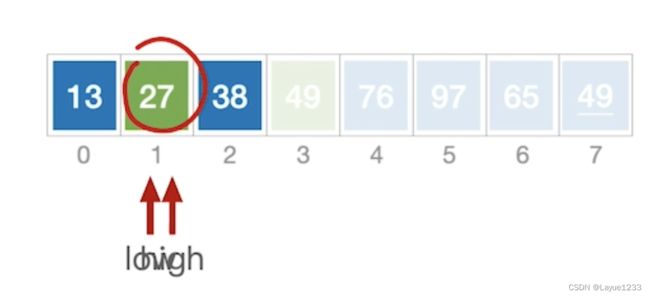
因此,我们返回low=1这个值
弹出Partition栈顶工作记录,如下图所示:
递归工作栈:Partition函数退出之后,pospivot=1。刚才处理Partition函数是执行到了第96行,所以接下来我们需要执行的是第97行。
因此,调用到第三层QuickSort函数,此时传入的参数是(A,0,0)。
这里QuickSort函数不会调用Partition函数,那由于low=high,就说明此时这个子表当中只有一个元素,那么一个元素肯定就不需要再进行排序了。递归结束!!
第三层QuickSort

第二层是执行到97行,因此现在执行第98行(注意递归工作栈修改97->98)
执行98行代码的时候,再进入第三层QuickSort排序,low=high,那么什么都不用做,返回(即弹出栈顶第三层)
执行完98行代码之后(记录的#98),第二层QuickSort函数也执行完毕,弹出栈顶第二层的元素。
那么递归工作栈将会只有第一层QuickSort函数:
之前这个函数运行到了97行代码,那么接下来应该运行到98行,即: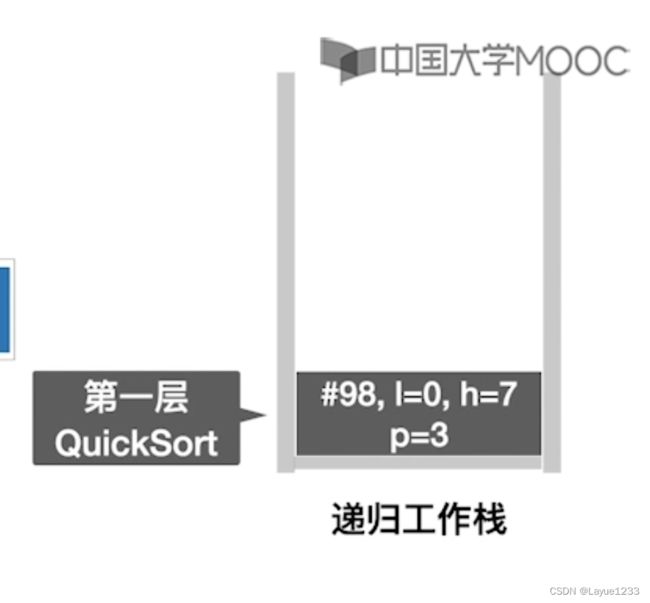
根据栈顶记录:这里第98行代码传入的参数是(A,4,7)。
(注意:此时根据前面的左子表递归,已经使得49左边的子表已经运有序。)
执行第98行代码:low =4,high=7。产生第二层QuickSort函数,第二层QS函数满足if语句,因此执行第96行语句,调用Partition函数,因此栈顶信息再加上#96.并且压入Partition函数(A,4,7),返回一个low = 6;那么返回到上一层函数之后(即第二层QS函数),由于运行,了#96Partition函数,那么接下来该运行的是97,所以加入栈顶信息:#97,并加入pospivot=6信息
即:下图的递归工作栈(实际上是#97,只是这里暂时没修改) 第二层QS函数执行完96执行97调用第三层QS函数
第二层QS函数执行完96执行97调用第三层QS函数
第三层QS函数满足if语句,调用Partition函数,即:
左边是Partition函数完成的功能,返回low=4;弹出栈顶,并将第三层的QS函数信息修改成#97(因为已经调用了Partition函数(第96行)),并且加入信息pospivot=4.
运行97行代码,第三层QS函数将会调用第四层QS函数(A,low=4,h=p-1=3)也就是说,此时low的值大于了high的值
即: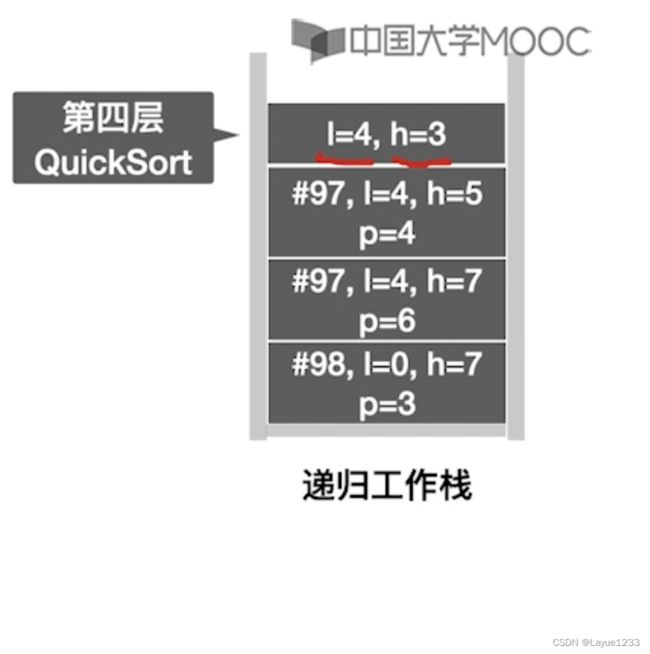
这就说明:
所以这种情况下,仍然是不满足low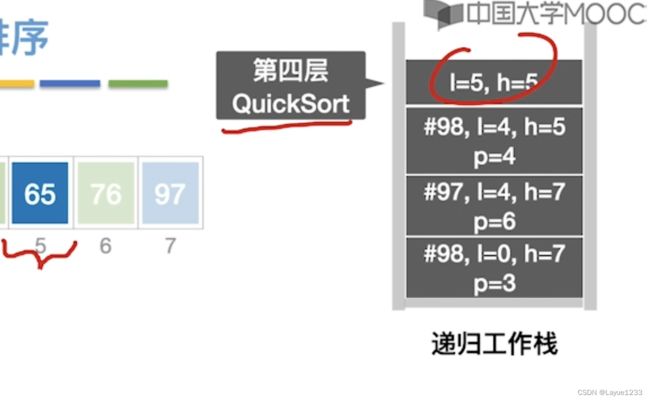
此时由于第四层QS(A,5,5)不满足if语句的条件,因此什么都不会做就直接返回上一层。
因此,到目前为止,第四层返回了第三层,第三层也已经执行完了98行代码,也会返回上一层递归。因此递归工作栈变为:
根据记录,这一层QS函数,已经运行完了第97行,那么接下来该运行98行。

此时递归的过程已经全部完成了,0-7的子表也全部变成了有序的序列。
算法效率分析:
1.时间复杂度:第一层QS函数是要处理0-7这个范围内的这些元素,其实就是要处理0-7这个范围内的这些元素,对他们进行一次划分,也就是对0-7调用一次partition函数。
而对于par。 所要做的就是用lowhigh指针不断地向中间移动,因此par函数的执行就是把这n个元素扫描一遍,他的时间复杂度是不超过n的这样一个数量级(个人觉得就是n)
那么经过一次划分之后,第二层的QS会对0-2以及4-7这两个区间分别调用一次Partition函数(其实通过前面对递归工作栈的分析过程可以看出,虽然是先左递归,但是第二层QS这层元素上面,最终会有右递归以及右递归的一系列左递归栈元素)
由于0-2以及4-7这两个区间的元素都是小于n的,那么如果调用partition函数它的时间复杂度必定是小于o(n)这个数量级。
接下来,请自己分析下下图的内容:
所以从上个例子,可以看出我们最多进行四层QS函数调用,然后每一层QS其实只需要处理剩下的这些还没有确定最终位置的元素,而这些还没有排好序的元素他们的数量是小于n,因此对这些元素额处理总的时间复杂度都不会超过n这个数量级。那么每一层的QS调用都不会超过on,所以总的时间复杂度就可以用on乘以递归的层数就可以得到。
而空间复杂度也是由递归调用工作栈深度来决定。(从上面的分析过程就可以看出)
因此空间复杂度是和递归层数深度是呈正相关的。
可以看到每层QS都会把当前的子区间再次划分成左右两个部分。
因此我们就会得到一个二叉树:
而这个二叉树的层数就是对应着递归调用的深度。
因此我们就可以把问题转换为一颗结点为n的二叉树的高度的上限和下限的一个判断:(见右下角)
比较好的情况(我们刚刚那个例子)
最坏的情况:元素全部已经递增有序

每一次QS中Partition函数都会扫描n的数量级(从右往左依次扫描会扫描完整个表)
每次划分都是使得左边的子表什么都没有,这样是很不均匀的。
因此一共需要八层QS函数调用
递归层数增加,效率降低。
所以有n个元素最多要进行n次QS函数调用。
基于上方的理解:我们只需要知道快速排序能够有以下的改进思想即可,即:让划分更加均匀一些。
随机选一个元素作为基准,那么从概率上讲就不太可能选择到最小的或者最大的元素。
快速排序的稳定性:
调用一次int Partition函数之后,Partition函数会将2 2’ 1变成 1 2’ 2
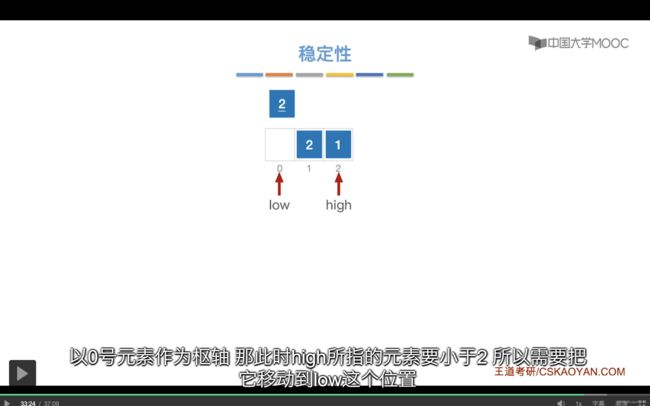

可以看到这个算法是不稳定的。
快速排序的算法一定要完完整整写出来代码!
一次划分指的是对一个子表调用一次Patition函数得到的最终的low值(即枢纽放置的位置)
一次划分只能确定一个值
一趟排序是指的是某一层的QuickSort函数调用;它可以确定多个元素的最终位置。