高阶数据结构图上篇

图的基本概念

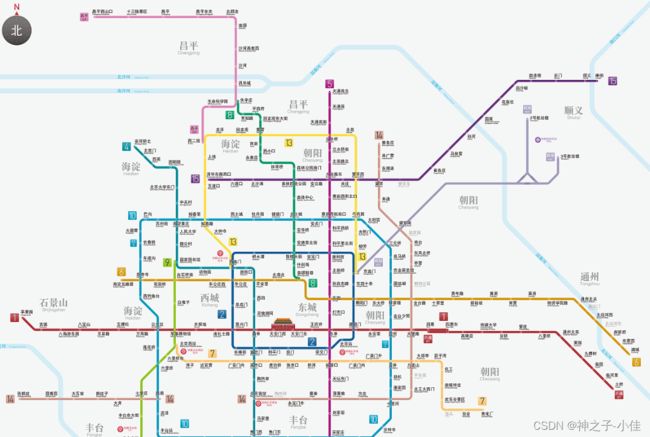
图是由顶点集合及顶点间的关系组成的一种数据结构：G=(V,E),G表示个图，V是图G中顶点的集合，E是图G中边的集合。就好比我们每天生活中乘坐的地铁，各个轨道相连接组成的地铁路线图就是一个抽象的图！

图和树的区别是什么？

1.树是一种特殊的图，图不一定是树
2.树关注的是节点中存的值，图关注的是顶点及边的权值
3.树可以是空树，但图不可以是空图，至少有一个顶点

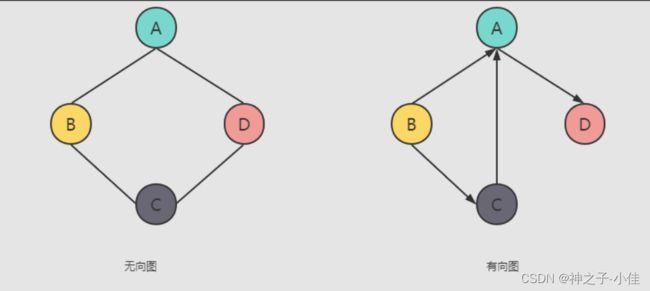
无向图和有向图的概念：

在图中，若用箭头标明了边是有方向性的，则称这样的图为有向图，否则称为无向图。

权值

权值就是定义的路径上面的值,它的英文是weight，所以有的书上也叫权重。可以这样理解为节点间的距离,通常指字符对应的二进制编码出现的概率。边的权值就是边的权重，其意义表示链接两个结点的边的大小或者长度等。这里我们有红色数字1-8表示权值。

邻接矩阵是什么？

邻接矩阵是表示顶点之间相邻关系的矩阵，设G=(V,E)是一个图，这个图G表示V和E集合，其中，V是顶点，E是边。因此，用一个一维数组存放图中所有顶点数据；用一个二维数组存放顶点间关系（边或弧）的数据，这个二维数组称为邻接矩阵。邻接矩阵又分为有向图邻接矩阵和无向图邻接矩阵。

如图所示，顶点0和顶点1之间有边关联，那么矩阵中的元素A[0][1]与A[1][0]的值就是1；顶点A和顶点C之间没有边关联，那么矩阵中的元素A[0][2]与A[2][0]的值就是0。像这样表达图中顶点关联关系的矩阵，就叫做邻接矩阵。需要注意的是，矩阵从左上到右下的一条对角线，对角线上面的元素都是0，这样很容易想明白：任何一个顶点与它自身是没有连接的。同时，无向图对应的矩阵是一个对称矩阵，A和B有关联，那么B和A也必定有关联，因此A[0][1]和A[1][0]的值一定相等。

邻接矩阵的特点

1.邻接矩阵存储方式非常适合稠密图
2.领接矩阵O(1)判断另个顶点的链接关系
3.相对而言不适合查一个顶点连接所有边

有向图和无向图的邻接矩阵有什么区别？

一、对称区别：
1、无向图的邻接矩阵是对称的。
2、有向图的邻接矩阵不一定对称。

二、元素区别：
1、对于无向图，顶点V1的度是邻接矩阵中第i行（或第i列）的非零元素的个数。
2、对于有向图，顶点V1的度是邻接矩阵中第i行和第i列的非零元素的个数之和。

邻接表是什么？

使用数组表示顶点的集合，使用链表表示边的关系，比如我们可以使用vector保存所有的顶点，使用链表保存与每个顶点连通的顶点。

邻接表的特点

1.适合存储稀疏图
2.适合查找一个顶点链接出去的边
3.不适合确顶两个顶点是否相连及权值

代码实现

#pragma once
#include
#include
//weight
namespace matrix
{
	//false表示无向图,true表示有向图
	//MAX_W是非类型的模板参数
	template<class V, class W, W MAX_W = INT_MAX, bool Direction = false>
	class Graph
	{
	public:
		Graph()
		{}
		//手动添加边
		Graph(const V* a, size_t n)
		{
			//如果 n 比当前 vector 容器的容量小，则该方法什么也不会做；反之如果 n 比当前 vector 容器的容量大，则 vector 容器就会扩容。
			_vertexs.reserve(n);
			for (size_t i = 0; i < n; ++i)
			{
				_vertexs.push_back(a[i]);//存顶点
				_indexMap[a[i]] = i;//顶点找下标
			}
			_matrix.resize(n);

			for (size_t i = 0; i < _matrix.size(); ++i)
			{
				_matrix[i].resize(n, MAX_W);
			}
		}
		size_t GetVerIndex(const V& v)//顶点的下标
		{
			auto it = _indexMap.find(v);
			if (it != _indexMap.end())
			{
				return it->second;
			}
			else
			{
				throw invalid_argument("顶点不存在");

				return -1;
			}
		}

		void AddEdge(const V& src, const V& dst, const W& w)
		{
			size_t srci = GetVerIndex(src);
			size_t dsti = GetVerIndex(dst);

			_matrix[srci][dsti] = w;
			//false表示无向图
			if (Direction == false)
			{
				_matrix[dsti][srci] = w;//w表示这个权值
			}
		}

		void Print()
		{
			for (size_t i = 0; i < _vertexs.size(); ++i)
			{
				cout << "[" << i << "]" << "->" << _vertexs[i] << endl;
			}
			cout << endl;

			//矩阵
			//打印横下标
			cout << "  ";
			for (size_t i = 0; i <_vertexs.size(); ++i)
			{
				cout << i <<" ";
			}
			cout << endl;

			for (size_t i = 0; i < _matrix.size(); ++i)
			{
				cout << i << " ";//竖下标
				for (size_t j = 0; j < _matrix.size(); ++j)
				{
					//cout << _matrix[i][j] << " ";
					if (_matrix[i][j] == MAX_W)
					{
						cout << "* ";
					}
					else
					{
						cout << _matrix[i][j] << " ";

					}
				}
				cout << endl;
			}
			cout << endl;

		}


	private:
		vector<V> _vertexs;//顶点集合
		map<V, int> _indexMap;//顶点映射下标关系
		vector<vector<W>> _matrix;//邻接矩阵
	};

		void TestGraph1()
		{
			Graph<char, int, INT_MAX, true> g("0123", 4);
			g.AddEdge('0', '1', 1);
			g.AddEdge('0', '3', 4);
			g.AddEdge('1', '3', 2);
			g.AddEdge('1', '2', 9);
			g.AddEdge('2', '3', 8);
			g.AddEdge('2', '1', 5);
			g.AddEdge('2', '0', 3);
			g.AddEdge('3', '2', 6);
			g.Print();

		}
}

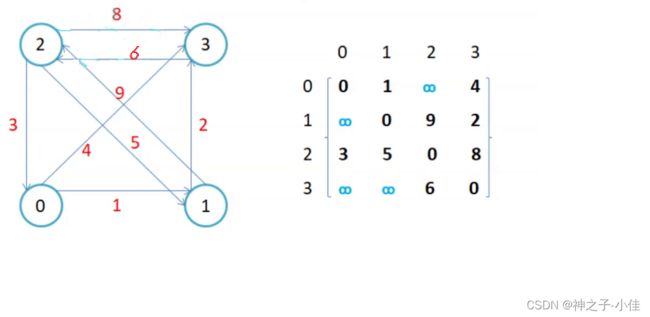
图中这样打印可下标可以清楚的看到顶点0和3是相连的，它们的权值是4,顶点1和3是相连的，它们的权值是2，顶点0和1相连它们的权值是1等。

总结

邻接矩阵和领接表其实属于相辅相成的，各有优缺点的互补结构。