数值分析——Hermite插值
埃尔米特(Hermite)插值
为什么需要Hermite插值
在部分插值应用中,不仅要求数据点函数值相等,还要求若干阶导数相同,满足函数值和若干导数值都相等的插值法成为Hermite插值。课件里只考虑了一阶导数相等情况。
从差商看牛顿插值与泰勒插值与Hermite插值
回忆一下差商定义: f [ x 0 , x 1 ] = f ( x 1 ) − f ( x 0 ) x 1 − x 0 f[x_0,x_1]=\dfrac{f(x_1)-f(x_0)}{x_1-x_0} f[x0,x1]=x1−x0f(x1)−f(x0)
如果一阶重节点差商定义为: f [ x 0 , x 0 ] = lim x 1 → x 0 f ( x 1 ) − f ( x 0 ) x 1 − x 0 = f ′ ( x 0 ) f[x_0,x_0]=\lim\limits_{x_1\to x_0}\dfrac{f(x_1)-f(x_0)}{x_1-x_0}=f'(x_0) f[x0,x0]=x1→x0limx1−x0f(x1)−f(x0)=f′(x0)
可以找到规律, n n n阶重节点差商则为: f [ x 0 , x 0 , . . . , x 0 ] = f ( n ) ( x 0 ) n ! f[x_0,x_0,...,x_0]=\dfrac{f^{(n)}(x_0)}{n!} f[x0,x0,...,x0]=n!f(n)(x0)
此时,如果对 n + 1 n+1 n+1个 x 0 x_0 x0进行牛顿插值,可得到函数 f ( x 0 ) f(x_0) f(x0)在 x 0 x_0 x0点的泰勒展开。也叫泰勒插值,实际上这也可以被视为一个点的 n n n次Hermite插值。
三点三次Hermite插值
三点三次Hermite插值是对三个数据点 x 0 , x 1 , x 2 x_0,x_1,x_2 x0,x1,x2进行插值(注意,这里数据点数是固定的),不仅要求插值函数与函数值相等,还要求 p ′ ( x 1 ) = f ′ ( x 1 ) p'(x_1)=f'(x_1) p′(x1)=f′(x1)。
**如何进行三点三次Hermite插值?**根据三点三次Hermite插值的条件与牛顿插值相比,仅仅多出一个条件 p ′ ( x 1 ) = f ′ ( x 1 ) p'(x_1)=f'(x_1) p′(x1)=f′(x1)。因此,我们只需要增加一个由这个导数相等的方程确定的参量就可以满足条件。首先,因为牛顿插值已经做到三点的函数值相等,因此在这三点处增加的这一项一定是0。因此可以设出增加的这一项是: α ( x − x 0 ) ( x − x 1 ) ( x − x 2 ) \alpha(x-x_0)(x-x_1)(x-x_2) α(x−x0)(x−x1)(x−x2)。
因此三点三次Hermite插值多项式为 p ( x ) = f ( x 0 ) + f [ x 0 , x 1 ] ( x − x 0 ) + f [ x 0 , x 1 , x 2 ] ( x − x 0 ) ( x − x 1 ) + α ( x − x 0 ) ( x − x 1 ) ( x − x 2 ) p(x)=f(x_0)+f[x_0,x_1](x-x_0)+f[x_0,x_1,x_2](x-x_0)(x-x_1)+\alpha(x-x_0)(x-x_1)(x-x_2) p(x)=f(x0)+f[x0,x1](x−x0)+f[x0,x1,x2](x−x0)(x−x1)+α(x−x0)(x−x1)(x−x2)
只需要用方程: p ′ ( x 1 ) = f ′ ( x 1 ) p'(x_1)=f'(x_1) p′(x1)=f′(x1)确定参量 α \alpha α就可以得到最终的插值函数。
带入很容易求得: α = f ′ ( x 1 ) − f [ x 0 , x 1 ] − f [ x 0 , x 1 , x 2 ] ( x 1 − x 0 ) ( x 1 − x 0 ) ( x 1 − x 2 ) \alpha=\dfrac{f'(x_1)-f[x_0,x_1]-f[x_0,x_1,x_2](x_1-x_0)}{(x_1-x_0)(x_1-x_2)} α=(x1−x0)(x1−x2)f′(x1)−f[x0,x1]−f[x0,x1,x2](x1−x0)
为什么三点三次插值和牛顿插值明显不一样
同是多项式插值,之前证明过多项式插值的唯一性,但为什么三点三次Hermite插值和牛顿插值并不同,这和我们之前证明过的多项式插值唯一性矛盾吗?
实际上,之前证明的多项式插值唯一性是对 n + 1 n+1 n+1个数据点,插值多项式最高阶为 n n n,三点三次插值有三个数据点,插值多项式最高阶也是3,并不是之前证明的那类插值,所以不同。
三点三次Hermite插值的代码示例
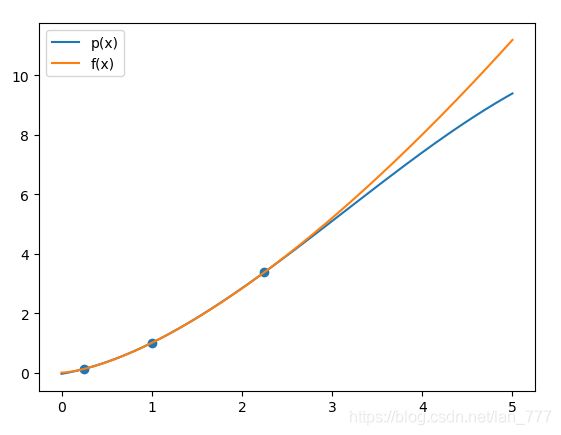
函数 f ( x ) = x 3 2 f(x)=x^{\frac{3}{2}} f(x)=x23,插值点 x 0 = 1 4 x_0=\frac{1}{4} x0=41, x 1 = 1 x_1=1 x1=1, x 2 = 9 4 x_2=\frac{9}{4} x2=49, f ′ ( 1 ) = 3 2 f'(1)=\frac{3}{2} f′(1)=23
import numpy as np
import matplotlib.pyplot as plt
# 函数f(x)=x^(3/2)
# 取三点:x0=1/4 x1=1 x2=9/4 f'(1)=3/2
xdata = np.array([1/4, 1, 9/4])
ydata = xdata**(3/2)
# 导数
df_x1 = 3/2
f_x0 = ydata[0]
first_diff = np.diff(ydata)/np.diff(xdata)
f_x0_x1 = first_diff[0]
print(np.diff(first_diff))
second_diff = np.diff(first_diff)/(xdata[-1]-xdata[0])
print(np.diff(first_diff))
print(np.diff(xdata[-2:]))
f_x0_x1_x2 = second_diff[0]
a = (df_x1-f_x0_x1-f_x0_x1_x2*np.diff(xdata)[0])/(-np.diff(xdata)[0] * np.diff(xdata)[1])
factor = np.array([f_x0, f_x0_x1, f_x0_x1_x2, a])
print(factor)
# 计算第k阶基函数
# 计算插值函数
def px(factor, x, xdata, ydata):
w = np.zeros((len(x), len(factor)))
wk = np.ones(len(x))
for i in range(len(factor)):
w[:,i] = wk
if i < len(factor)-1:
wk = wk*(x-xdata[i])
return w@factor
plot_x = np.linspace(0, 5, 400)
plot_y = px(factor, plot_x, xdata, ydata)
p1, = plt.plot(plot_x, plot_y)
p2, = plt.plot(plot_x, plot_x**(3/2))
p3 = plt.scatter(xdata, ydata)
plt.legend([p1, p2], ["p(x)", "f(x)"])
plt.show()
两点三次Hermite插值
两点三次Hermite插值是对两个数据点 x 0 , x 1 x_0, x_1 x0,x1进行插值,要求这两个点的插值函数值与原函数值相等且一阶导数相等。
这里是两个点的插值问题,插值条件可以写为: p ( x i ) = f ( x i ) = y i , p ′ ( x i ) = f ′ ( x i ) = m i , i = 0 , 1 p(x_i)=f(x_i)=y_i, p'(x_i)=f'(x_i)=m_i, i=0,1 p(xi)=f(xi)=yi,p′(xi)=f′(xi)=mi,i=0,1。
这里不能用三点三次插值的思想,因为如果用类似思路,这里有四个方程,需要确定两个待定系数。我们如果同样用牛顿插值多加两项待定系数乘 ( x − x 0 ) ( x − x 1 ) (x-x_0)(x-x_1) (x−x0)(x−x1),那这两个待定系数合并成一个了,所以构造不出。
构造的思路还是通过这四个方程来,我们首先意识到,这个插值多项式仍然是四项系数乘以基函数的累加。如果我们认为,四个系数就是 [ y 0 , y 1 , m 0 , m 1 ] [y_0, y_1,m_0,m_1] [y0,y1,m0,m1],那基函数应当满足什么条件?
现在设四项基函数为 a 0 ( x ) , a 1 ( x ) , b 0 ( x ) , b 1 ( x ) a_0(x),a_1(x),b_0(x),b_1(x) a0(x),a1(x),b0(x),b1(x),那么,根据方程必然有:
a 0 ( x 0 ) = 1 , a 1 ( x 0 ) = 0 , b 0 ( x 0 ) = 0 , b 1 ( x 0 ) = 0 a_0(x_0) = 1,a_1(x_0)=0,b_0(x_0)=0,b_1(x_0)=0 a0(x0)=1,a1(x0)=0,b0(x0)=0,b1(x0)=0
a 0 ( x 1 ) = 0 , a 1 ( x 1 ) = 1 , b 0 ( x 1 ) = 0 , b 1 ( x 1 ) = 0 a_0(x_1) = 0,a_1(x_1)=1,b_0(x_1)=0,b_1(x_1)=0 a0(x1)=0,a1(x1)=1,b0(x1)=0,b1(x1)=0
a 0 ′ ( x 0 ) = 0 , a 1 ′ ( x 0 ) = 0 , b 0 ′ ( x 0 ) = 1 , b 1 ′ ( x 0 ) = 0 a_0'(x_0) = 0,a_1'(x_0)=0,b_0'(x_0)=1,b_1'(x_0)=0 a0′(x0)=0,a1′(x0)=0,b0′(x0)=1,b1′(x0)=0
a 0 ′ ( x 1 ) = 0 , a 1 ′ ( x 1 ) = 0 , b 0 ′ ( x 1 ) = 0 , b 1 ′ ( x 1 ) = 1 a_0'(x_1) = 0,a_1'(x_1)=0,b_0'(x_1)=0,b_1'(x_1)=1 a0′(x1)=0,a1′(x1)=0,b0′(x1)=0,b1′(x1)=1
现在考虑 a 0 ( x ) a_0(x) a0(x)具体形式,因为 a 0 ( x 0 ) = 1 , a 0 ( x 1 ) = 0 a_0(x_0)=1,a_0(x_1)=0 a0(x0)=1,a0(x1)=0,可推断出 a 0 ( x ) a_0(x) a0(x)必然含有一项 x − x 1 x 0 − x 1 \dfrac{x-x_1}{x_0-x_1} x0−x1x−x1。
应当意识到,最终的插值多项式应该是个三次多项式, a 0 ( x ) a_0(x) a0(x)最高次项必然是 3 3 3。所以可以设 a 0 ( x ) a_0(x) a0(x)为 ( a x + b ) ( c x + d ) ( x − x 1 x 0 − x 1 ) (ax+b)(cx+d)(\dfrac{x-x_1}{x_0-x_1}) (ax+b)(cx+d)(x0−x1x−x1)或 ( a x + b ) ( x − x 1 x 0 − x 1 ) 2 (ax+b){(\dfrac{x-x_1}{x_0-x_1})}^2 (ax+b)(x0−x1x−x1)2,显然后者容易计算,先看看后者能不能解出满足要求的函数。
用Mathematica计算得: { a → − 2 x 0 − x 1 , b → − x 1 − 3 x 0 x 0 − x 1 } \left\{a\to -\dfrac{2}{{x_0}-{x_1}},b\to -\dfrac{{x_1}-3 {x_0}}{{x_0}-{x_1}}\right\} {a→−x0−x12,b→−x0−x1x1−3x0}
其他同理可以求得:
a 0 ( x ) = ( 1 + 2 x − x 0 x 1 − x 0 ) ( x − x 1 x 0 − x 1 ) 2 a_0(x)=(1+2\dfrac{x-x_0}{x_1-x_0}){(\dfrac{x-x_1}{x_0-x_1})}^2 a0(x)=(1+2x1−x0x−x0)(x0−x1x−x1)2
a 1 ( x ) = ( 1 + 2 x − x 1 x 0 − x 1 ) ( x − x 0 x 1 − x 0 ) 2 a_1(x)=(1+2\dfrac{x-x_1}{x_0-x_1}){(\dfrac{x-x_0}{x_1-x_0})}^2 a1(x)=(1+2x0−x1x−x1)(x1−x0x−x0)2
b 0 ( x ) = ( x − x 0 ) ( x − x 1 x 0 − x 1 ) 2 b_0(x)=(x-x_0){(\dfrac{x-x_1}{x_0-x_1})}^2 b0(x)=(x−x0)(x0−x1x−x1)2
b 1 ( x ) = ( x − x 1 ) ( x − x 0 x 1 − x 0 ) 2 b_1(x)=(x-x_1){(\dfrac{x-x_0}{x_1-x_0})}^2 b1(x)=(x−x1)(x1−x0x−x0)2
插值多项式为: H 3 ( x ) = y 0 a 0 ( x ) + y 1 a 1 ( x ) + m 0 b 0 ( x ) + m 1 b 1 ( x ) H_3(x)=y_0a_0(x)+y_1a_1(x)+m_0b_0(x)+m_1b_1(x) H3(x)=y0a0(x)+y1a1(x)+m0b0(x)+m1b1(x)
两点三次Hermite插值代码示例
import numpy as np
import matplotlib.pyplot as plt
# 函数f(x)=x^(3/2)
# 取两点:x0=1/4 x1=1
x0 = 1/4
x1 = 1
y0 = x0**(3/2)
y1 = x1**(3/2)
m0 = 3/2*x0**(1/2)
m1 = 3/2*x1**(1/2)
xdata = [x0, x1]
def px(factor, plot_x, xdata):
a0 = (1+2*(plot_x-xdata[0])/(xdata[1]-xdata[0]))*((plot_x-xdata[1])/(xdata[0]-xdata[1]))**2
a1 = (1+2*(plot_x-xdata[1])/(xdata[0]-xdata[1]))*((plot_x-xdata[0])/(xdata[1]-xdata[0]))**2
b0 = (plot_x-xdata[0])*((plot_x-xdata[1])/(xdata[0]-xdata[1]))**2
b1 = (plot_x - xdata[1])*((plot_x - xdata[0]) / (xdata[1] - xdata[0])) ** 2
return factor[0]*a0+factor[1]*a1+factor[2]*b0+factor[3]*b1
plot_x = np.linspace(0, 5, 400)
plot_y = px([y0,y1,m0,m1], plot_x, xdata)
p1, = plt.plot(plot_x, plot_y)
p2, = plt.plot(plot_x, plot_x**(3/2))
p3 = plt.scatter(xdata, [y0, y1])
plt.legend([p1, p2], ["p(x)", "f(x)"])
plt.show()