多元高斯分布/高斯过程全解析

大纲

• 公式推导
• 参数估计
• 高斯分布运算
• 高斯分布性质
• 高斯过程（Gaussian process）
• 高斯混合模型

概念区分

• 边缘分布(marginal distribution)和联合分布
• 概率密度函数和概率分布函数

1. 多元高斯分布公式推导

首先我们知道一元高斯分布是：$N(x|u,{\sigma }^2)=\frac{1}{\sqrt{2\pi {\sigma }^2}}exp[-\frac{1}{2{\sigma }^2}(x-u{)}^2]$, 拓展到高维时：
$$N(\overline{x}|\overline{u},\Sigma )=\frac{1}{(2\pi {)}^{D/2}}\frac{1}{|\Sigma {|}^{1/2}}exp[-\frac{1}{2}(\overline{x}-\overline{u}{)}^T{\Sigma }^{-1}(\overline{x}-\overline{u})]$$其中，$\overline{x}$ 表示维度为 D 的向量，$\overline{u}$ 则是这些向量的平均值，$\Sigma$ 表示所有向量 $\overline{x}$ 的协方差矩阵。

现在进行推导。为了简单起见，假设所有变量都是相互独立的，即对于概率分布函数 $f(x_0,x_1,\dots ,x_n)=f(x_0)f(x_1)...f(x_n)$ 成立。

假设有很多变量 $\overline{x}=\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]$，它们的均值为 $\overline{u}=\left[\begin{array}{c}{u}_1\\ u_2\end{array}\right]$，方差为 $\overline{\sigma }=\left[\begin{array}{c}{\sigma }_1\\ {\sigma }_2\end{array}\right]$。

由于 $x_1$，$x_2$ 是相互独立的，所以，$\overline{x}$ 的高斯分布函数可以表示为：
$$\begin{array}{rl}f(\overline{x})& =f(x_1,x_2)\\ & =f(x_1)f(x_2)\\ & =\frac{1}{\sqrt{2\pi {\sigma }_1^2}}exp(-\frac{1}{2}(\frac{x_1-u_1}{{\sigma }_1}{)}^2)\times \frac{1}{\sqrt{2\pi {\sigma }_2^2}}exp(-\frac{1}{2}(\frac{x_2-u_2}{{\sigma }_2}{)}^2)\\ & =\frac{1}{(2\pi {)}^{2/2}({\sigma }_1^2{\sigma }_2^2{)}^{1/2}}exp(-\frac{1}{2}[(\frac{x_1-u_1}{{\sigma }_1}{)}^2+(\frac{x_2-u_2}{{\sigma }_2}{)}^2])\end{array}$$接下来，为了推出文章开篇的高维公式，我们要想办法得到协方差矩阵 $\Sigma$。
对于二维的向量 $\overline{x}$ 而言，其协方差矩阵为：
$$\begin{array}{rlr}\Sigma & =& \left[\begin{array}{cc}{\sigma }_{11}& {\sigma }_{12}\\ {\sigma }_{12}& {\sigma }_{22}\end{array}\right]\\ & =& \left[\begin{array}{cc}{\sigma }_1^2& {\sigma }_{12}\\ {\sigma }_{21}& {\sigma }_2^2\end{array}\right]\end{array}$$

协方差（Covariance）在概率论和统计学中用于衡量两个变量的总体误差。而方差是协方差的一种特殊情况，即当两个变量是相同的情况。简单来讲，协方差就是衡量两个变量相关性的变量。当协方差为正时，两个变量呈正相关关系（同增同减）；当协方差为负时，两个变量呈负相关关系（一增一减）。 而协方差矩阵，只是将所有变量的协方差关系用矩阵的形式表现出来而已。通过矩阵这一工具，可以更方便地进行数学运算。协方差公式为：
$$Cov(X,Y)=E(X,Y)-E(X)E(Y)=\frac{{\sum }_{i=1}^n(x_i-\overline{x})(y_i-\overline{y})}{n-1}$$ 这里的 $X$，$Y$表示两个变量空间。用机器学习的话讲，就是样本有 $x$ 和 $y$ 两种特征，而 $X$ 就是包含所有样本的 $x$ 特征的集合，$Y$就是包含所有样本的 $y$ 特征的集合。$\overline{x}$ 和 $\overline{y}$ 是 $X$，$Y$ 两个特征空间的平均值。
那么假如 $Z$ 是包含$X$和$Y$的矩阵，那么计算协方差矩阵时，$$Cov(Z)=\mathrm{E}\left[(X-\mathrm{E}[X])(Y-\mathrm{E}[Y]{)}^{\top }\right]=\left[\begin{array}{cc}Cov(X,X)& Cov(X,Y)\\ Cov(Y,X)& Cov(Y,Y)\end{array}\right]$$
这样矩阵中之中每个元素 ${\Sigma }_{ij}=\frac{(样本矩阵第i列-第i列均值{)}^T(样本矩阵第j列-第j列均值)}{样本数-1}$
当$X$, $Y$两个变量独立时，$Cov(X,Y)$为0：
$$\begin{array}{rl}E(XY)& =\sum _x\sum _{y}x\times y\times p(x,y)\\ & =\sum _x\sum _{y}x\times y\times p_x(x)\times p_y(y)\\ & =\sum _{x}x\times p_x(x)\sum _{y}y\times p_y(y)\\ & =E(X)E(Y)\end{array}$$

由于 $x_1$，$x_2$ 是相互独立的，所以 ${\sigma }_{12}={\sigma }_{21}=0$。这样，$\Sigma$ 退化成 $\left[\begin{array}{cc}{\sigma }_1^2& 0\\ 0& {\sigma }_2^2\end{array}\right]$。
则 $\Sigma$ 的行列式 $|\Sigma |={\sigma }_1^2{\sigma }_2^2$，代入公式 (4) 就可以得到：
$$f(\overline{x})=\frac{1}{(2\pi {)}^{2/2}|\Sigma {|}^{1/2}}exp(-\frac{1}{2}[(\frac{x_1-u_1}{{\sigma }_1}{)}^2+(\frac{x_2-u_2}{{\sigma }_2}{)}^2])$$
这样一来，我们已经推出了公式的左半部分，下面，开始处理右面的 exp 函数。
原始的高维高斯函数的 exp 函数为：$exp[-\frac{1}{2}(\overline{x}-\overline{u}{)}^T{\Sigma }^{-1}(\overline{x}-\overline{u})]$，根据前面算出来的 $\Sigma$，我们可以求出它的逆：${\Sigma }^{-1}=\frac{1}{{\sigma }_1^2{\sigma }_2^2}\left[\begin{array}{cc}{\sigma }_2^2& 0\\ 0& {\sigma }_1^2\end{array}\right]$。
接下来根据这个二维的例子，将原始的 exp() 展开：
$$\begin{array}{rl}exp[-\frac{1}{2}(\overline{x}-\overline{u}{)}^T{\Sigma }^{-1}(\overline{x}-\overline{u})]& =exp[-\frac{1}{2}\left[\begin{array}{c}{x}_1-u_1{x}_2-u_2\end{array}\right]\frac{1}{{\sigma }_1^2{\sigma }_2^2}\left[\begin{array}{cc}{\sigma }_2^2& 0\\ 0& {\sigma }_1^2\end{array}\right]\left[\begin{array}{c}{x}_1-u_1\\ x_2-u_2\end{array}\right]]\\ & =exp[-\frac{1}{2}\left[\begin{array}{c}{x}_1-u_1{x}_2-u_2\end{array}\right]\frac{1}{{\sigma }_1^2{\sigma }_2^2}\left[\begin{array}{c}{\sigma }_2^2(x_1-u_1)\\ {\sigma }_1^2(x_2-u_2)\end{array}\right]]\\ & =exp[-\frac{1}{2{\sigma }_1^2{\sigma }_2^2}[{\sigma }_2^2(x_1-u_1{)}^2+{\sigma }_1^2(x_2-u_2{)}^2]]\\ & =exp[-\frac{1}{2}[\frac{(x_1-u_1{)}^2}{{\sigma }_1^2}+\frac{(x_2-u_2{)}^2}{{\sigma }_2^2}]]\end{array}$$
展开到最后，发现推出了原公式。说明原公式 $N(\overline{x}|\overline{u},\Sigma )=\frac{1}{(2\pi {)}^{D/2}}\frac{1}{|\Sigma {|}^{1/2}}exp[-\frac{1}{2}(\overline{x}-\overline{u}{)}^T{\Sigma }^{-1}(\overline{x}-\overline{u})]$是成立的。

---

2. 参数估计

如果给定了很多数据点，并且知道它们服从某个高斯分布，我们要求高斯分布的参数（$\mu$ 和 $\Sigma$），估计模型参数的方法有很多，最常用的就是极大似然估计（MLE）。对于一维的高斯模型假如有m个数据点，则似然函数:
$$f(x_1,x_2,\dots ,x_m)=\prod _{i=1}^m\frac{1}{\sqrt{2\pi }\sigma }exp(-\frac{(x_i-\tilde{\mu }{)}^2}{2{\sigma }^2})$$取对数后求导，令导数为 0 得到似然方程。$$\frac{\partial \ln f}{\partial \overline{\mu }}=\frac{1}{{\sigma }^2}\sum _{i=1}^m(x_i-\tilde{\mu })=0$$$$\frac{\partial \ln f}{\partial \sigma }=-\frac{m}{\sigma }+\frac{1}{{\sigma }^3}\sum _{i=1}^m(x_i-\tilde{\mu })=0$$得到 $\tilde{\mu }=\frac{1}{m}{\sum }_{i=1}^m{x}_i$，$\sigma =\sqrt{\frac{1}{m}{\sum }_{i=1}^m(x_i-\tilde{\mu }{)}^2}$

多维高斯分布时，假如有m个p维向量 $x$，参数估计为：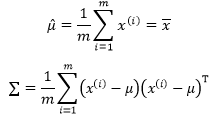
在计算样本协方差矩阵时，我们要使用无偏估计，即将分母由 $m$ 改为 $(m-1)$。[^1]

---

3. 高斯分布运算

3.1 一元高斯分布相乘

假设$p(x_1)=\mathcal{N}(x|{\mu }_1,{\sigma }_1),p(x_2)=\mathcal{N}(x|{\mu }_2,{\sigma }_2)$均是关于变量
$x$的分布，得两个高斯分布相乘仍为缩放的高斯分布：
$$\begin{array}{rl}p(x_1)p(x_2)& =e^{-\frac{1}{2{\sigma }_1^2}(x-{\mu }_1{)}^2}{e}^{-\frac{1}{2{\sigma }_2^2}(x-{\mu }_2{)}^2}\\ & =e^{-\frac{1}{2}\frac{（{\sigma }_1^2+{\sigma }_2^2）x^2-2({\mu }_1{\sigma }_2^2+{\mu }_2{\sigma }_1^2)x+\text{constant}}{{\sigma }_1^2{\sigma }_2^2}}\end{array}$$则高斯分布的参数: $$\begin{array}{rl}\mu & =\frac{{\mu }_1{\sigma }_2^2+{\mu }_2{\sigma }_1^2}{{\sigma }_1^2+{\sigma }_2^2},\sigma =\sqrt{\frac{{\sigma }_1^2{\sigma }_2^2}{{\sigma }_1^2+{\sigma }_2^2}}\end{array}$$上式可写为如下形式，从而推广至$n$个一维高斯分布相乘：$$\begin{array}{rl}\mu & =(\frac{{\mu }_1}{{\sigma }_1^2}+\frac{{\mu }_2}{{\sigma }_2^2}){\sigma }^2,\frac{1}{{\sigma }^2}=\frac{1}{{\sigma }_1^2}+\frac{1}{{\sigma }_2^2}\end{array}$$
新函数等价于正态分布 $N(\mu ,{\sigma }^2)$ 的概率密度函数乘以缩放因子 $A$ 。其中，缩放因子$A=\frac{e^{-\frac{{\left({\mu }_1-{\mu }_2\right)}^2}{2({\sigma }_1^2+{\sigma }_2^2)}}}{\sqrt{2\pi \left({\sigma }_1^2+{\sigma }_2^2\right)}}$

3.2 多元高斯分布相乘

$$\begin{array}{rl}\mathbf{\mu }& =\Sigma \left({\Sigma }_1^{-1}{\mathbf{\mu }}_1+{\Sigma }_2^{-1}{\mathbf{\mu }}_2\right)\\ \mathbf{\Sigma }& ={\left({\mathbf{\Sigma }}_1^{-1}+{\mathbf{\Sigma }}_2^{-1}\right)}^{-1}\end{array}$$

3.3 高斯分布相加

两个高斯分布函数直接相加，很明显不是一个高斯函数。如果两个满足高斯分布的随机变量相加，那么他们的和还是一个高斯分布。具体的，如果 $X\sim N({\mu }_X,{\sigma }_X^2)$, $Y\sim N({\mu }_Y,{\sigma }_Y^2)$，$Z=X+Y$ 那么 $$Z\sim N({\mu }_X+{\mu }_Y,{\sigma }_X^2+{\sigma }_Y^2)$$

需要用到卷积运算：$(f\ast g)(n)={\int }_{-\infty }^{\infty }f(\tau )g(n-\tau )d\tau$

$$\begin{array}{rl}{F}_Z(z)& =P(Z\le z)=P(X+Y\le z)\\ & ={\iint }_{x+y\le z}f(x,y)dxdy\\ & ={\int }_{-\infty }^{\infty }dx{\int }_{-\infty }^{z-x}f(x,y)dy\\ & \stackrel{\text{令u=y+x}}{=}{\int }_{-\infty }^{\infty }dx{\int }_{-\infty }^{z}f(x,u-x)du\\ & ={\int }_{-\infty }^{z}du{\int }_{-\infty }^{\infty }f(x,u-x)dx\end{array}$$ 所以，Z的概率密度函数为：
$$f_Z(z)={\int }_{-\infty }^{\infty }f(x,z-x)dx$$当$X，Y$为独立随机变量时，$Z$的概率密度为$f_Z(z)={\int }_{-\infty }^{\infty }{f}_Y(z-x)f_X(x)dx$

法二：使用特征函数证明
高斯分布的特征函数为：$$\phi (t)=\exp \left(it\mu -\frac{{\sigma }^2{t}^2}{2}\right)$$所以，
$$\begin{array}{rl}{\phi }_{X+Y}(t)=E\left(e^{it(X+Y)}\right)={\phi }_X(t){\phi }_Y(t)& =\exp \left(it{\mu }_X-\frac{{\sigma }_X^2{t}^2}{2}\right)\exp \left(it{\mu }_Y-\frac{{\sigma }_Y^2{t}^2}{2}\right)\\ & =\exp \left(it({\mu }_X+{\mu }_Y)-\frac{({\sigma }_X^2+{\sigma }_Y^2)t^2}{2}\right).\end{array}$$

3.4 高斯线性模型

$$\begin{array}{r}p(x)=\mathcal{N}({\mu }_0,{\mathbf{\Sigma }}_0)\\ p(y|x)=\mathcal{N}(Ax+b,{\Sigma }_y)\end{array}$$

---

4. 高斯分布性质

多元正态分布有4种等价的定义。

定义1–由标准正态随机向量线性组合得到

设 $U={\left(U_1,U_2,\cdots ,U_q\right)}^{\prime }$ 为随机向量， $U_1,\cdots ,U_q$ 独立服从标准正态。设 $\mu$ 为 $p$ 维常数向量， $A$ 为 $p\times q$ 维常数矩阵，则称 $X=AU+\mu$ 的分布为 $p$ 元正态分布，或称 $X$ 为 $p$ 维正态随机向量，记作 $X\sim N_p\left(\mu ,A{A}^{\prime }\right)$

性质1–特征函数

在概率论中，任何随机变量的特征函数（ch.f）完全定义了它的概率分布。在实直线上，它由以下公式给出，其中X是任何具有该分布的随机变量： ${\phi }_X(t)=E[e^{itX}]$
$$\begin{array}{rl}{\phi }_X(t)& =E[e^{itX}]\\ & \stackrel{\text{泰勒展开}}{=}E(1+\frac{itX}{1}-\frac{t^2{X}^2}{2!}+\cdots +\frac{(it{)}^n{X}^n}{n!})\\ & =E(1)+E(\frac{itX}{1})-E(\frac{t^2{X}^2}{2!})+\cdots +E(\frac{(it{)}^n{X}^n}{n!})\\ & =1+\frac{it\stackrel{\text{一阶矩}}{E[X]}}{1}-\frac{t^2\stackrel{\text{二阶矩}}{E[X^2]}}{2!}+\cdots +\frac{(it{)}^n\stackrel{\text{n阶矩}}{E[X^n]}}{n!})\end{array}$$

$k$阶原点矩: $E[X^k]或A_k=\frac{1}{n}{\sum }_{i=1}^n{X}_i^k,k=1,2,\cdots$
$k$阶中心矩: $E[(X-E(X){)}^k]或A_k=\frac{1}{n}{\sum }_{i=1}^n(X_i-\bar{X}{)}^k,k=2,3,\cdots$

可见特征函数包含了分布函数的所有矩（moment），也就是包含了分布函数的所有特征。
所以，特征函数其实是随机变量 $X$ 的分布的另外一种描述方式。
假设某连续随机变量 $X$的概率密度函数为 $f(x)$，那么可知：$E(X)={\int }_{-\infty }^{+\infty }xf(x)dx$，特征函数为:
$$\begin{array}{r}{\phi }_X(t)=E[e^{itX}]={\int }_{-\infty }^{+\infty }{e}^{itx}f(x)dx\end{array}$$ 特征函数把分布函数换到另外一个坐标系，也可以获得一些计算的好处：

• 假如我们不知道分布函数，但是通过实验算出了期望、方差、偏度、峰度等，那么可以用特征函数去代替分布函数
• 两个分布函数的卷积 $f\ast g$ 通过特征函数更换坐标系后，可以变为更容易计算的乘法：$\phi (f\ast g)=\phi (f)\phi (g)$
• 通过对 $t$ 求导，可以简单求出各阶矩：${\phi }_X^{(k)}(0)=i^{k}E[X^k]$

由定义1得到的随机向量 $X$ 的特征函数为
$${\Phi }_X(t)=\exp \left[i{t}^{\prime }\mu -\frac{1}{2}{t}^{\prime }A{A}^{\prime }t\right]$$其中 $t={\left(t_1,\cdots ,t_p\right)}^{\prime }\in {\mathbb{R}}^p$
证明：首先考虑一维标准正态分布的特征函数为 ${\Phi }_{U_i}\left(t_i\right)=\exp \left[-\frac{1}{2}{t}_i^2\right]$
根据独立性有
$${\Phi }_U(t)=\exp \left[-\frac{1}{2}\sum _{i=1}^q{t}_i^2\right]=\exp \left[-\frac{1}{2}{t}^{\prime }t\right]$$进而根据 X 的定义得到
$$\begin{array}{rl}{\Phi }_X(t)& =E[\exp \left\{i{t}^{\prime }X\right\}]=E[\exp \left\{i{t}^{\prime }(AU+\mu )\right\}]\\ & =E[\exp \left\{i{t}^{\prime }\mu \right\}]E[\exp \left\{i{t}^{\prime }AU\right\}]=E[\exp \left\{i{t}^{\prime }\mu \right\}]E[\exp \left\{i{\left(A^{\prime }t\right)}^{\prime }U\right\}]\end{array}$$其中 $E[\exp \left\{i{\left(A^{\prime }t\right)}^{\prime }U\right\}]$ 即 ${\Phi }_U(A^{\prime }t)$ ，代入即得结论.

定义2–由特征函数定义

如果随机向量 X 的特征函数具有如下形式 ${\Phi }_X(t)=\exp \left[i{t}^{\prime }\mu -\frac{1}{2}{t}^{\prime }\Sigma t\right]$, 则称 $X$ 服从 $p$ 维正态分布，记作 $X\sim N_p(\mu ,\Sigma )$

性质2–正态随机向量任意线性变换仍服从正态分布

设 $X\sim N_p(\mu ,\Sigma )$，令 $Z=BX+d$ ，则 $Z\sim N_s\left(B\mu +d,B\Sigma B^{\prime }\right)$ ，其中 $B$ 为 $s\times q$ 维矩阵，$d$ 为 $s$ 维向量.

推论–子向量的均值与协方差：

设 $X=\left[\begin{array}{c}{X}^{(1)}\\ X^{(2)}\end{array}\right]\begin{array}{c}r\\ p-r\end{array}\sim N_p(\mu ,\Sigma )$ ，将 $\mu$, $\Sigma$ 分为
$$\mu =\left[\begin{array}{c}{\mu }^{(1)}\\ {\mu }^{(2)}\end{array}\right]\begin{array}{c}r\\ p-r\end{array},\Sigma =\left[\begin{array}{cc}{\Sigma }_{11}& {\Sigma }_{12}\\ {\Sigma }_{21}& {\Sigma }_{22}\end{array}\right]\begin{array}{c}r\\ p-r\end{array}$$ 则有 $X^{(1)}\sim N_r\left({\mu }^{(1)},{\Sigma }_{11}\right),X^{(2)}\sim N_{p-r}\left({\mu }^{(2)},{\Sigma }_{22}\right)$
注意： ${\Sigma }_{12}\ne {\Sigma }_{21}$ ，两者互为转置

性质3–多元正态 $\iff$ 任意线性组合为一元正态

设 $X={\left(X_1,X_2,\cdots ,X_p\right)}^{\prime }$ 为 $p$ 维随机向量，则 $X$ 服从 $p$ 元正态分布等价于对任意 $p$ 维实向量， $\xi =a^{\prime }X$ 是一维正态随机变量.
证明：
当 X 为 p 元正态分布，由性质2知 $\xi$ 为一维正态随机变量。
反之，如果对任意 $a$ 有$\xi =a^{\prime }X$ 为一维正态随机变量，则 $\xi$ 各阶矩存在，进而 $X$ 的均值和协方差存在，分别设为 $\mu ,\Sigma$ ，则
$$\xi =a^{\prime }X\sim N\left(a^{\prime }\mu ,a^{\prime }\Sigma a\right)$$ 进而考察 X 的特征函数得到
$${\Phi }_X(a)=\exp \left[i{a}^{\prime }X\right]=\exp [i\xi ]={\Phi }_{\xi }(1)=\exp \left[\mathrm{i}{a}^{\prime }\mu -\frac{1}{2}{a}^{\prime }\Sigma a\right]$$ 刚好等于多元正态的特征函数，由特征函数与分布的一一对应得到结论.

定义3–任意线性组合为正态

如果 $p$ 维随机向量 $X$ 的任意线性组合均服从一元正态分布，则称 $X$ 为 $p$ 维正态随机向量.

性质4–联合密度函数

如果 $X\sim N_p(\mu ,\Sigma )$ 且 $\Sigma >0$ ，则 $X$ 的联合密度函数为
$$f(x)=\frac{1}{(2\pi {)}^{p/2}|\Sigma {|}^{1/2}}\exp \left[-\frac{1}{2}(x-\mu {)}^{\prime }{\Sigma }^{-1}(x-\mu )\right]$$

定义4–密度函数

如果 $p$ 维随机向量 $X$ 的联合密度函数为
$$f(x)=\frac{1}{(2\pi {)}^{p/2}|\Sigma {|}^{1/2}}\exp \left[-\frac{1}{2}(x-\mu {)}^{\prime }{\Sigma }^{-1}(x-\mu )\right]$$ 则称 $X$ 为 $p$ 维正态随机向量.
注意：定义4要求 $\Sigma >0$ ，其他三个只要求 $\Sigma \ge 0$ ，一般也不考虑 $X$ 为退化随机向量的情况.

5. 高斯条件分布和独立性

仅讨论 $\Sigma \ge 0$ (即半正定) 的情形

定理1–正态随机向量的独立性等价于协方差为0矩阵

定理2–条件分布

设 $X=\left[\begin{array}{c}{X}^{(1)}\\ X^{(2)}\end{array}\right]\begin{array}{c}r\\ p-r\end{array}\sim N_p(\mu ,\Sigma )(\Sigma >0)$ ，则当 $X^{(2)}=x^{(2)}$ 给定时， $X^{(1)}$ 的条件分布为
$$\left(X^{(1)}\mid X^{(2)}=x^{(2)}\right)\sim N_r\left({\mu }_{1\cdot 2},{\Sigma }_{11\cdot 2}\right)$$其中
$$\begin{array}{rl}{\mu }_{1\cdot 2}& ={\mu }^{(1)}+{\Sigma }_{12}{\Sigma }_{22}^{-1}\left(x^{(2)}-{\mu }^{(2)}\right)\\ {\Sigma }_{1\cdot 2}& ={\Sigma }_{11}-{\Sigma }_{12}{\Sigma }_{22}^{-1}{\Sigma }_{21}\end{array}$$
证明：从回归的角度会比较容易理解，理论依据是，在均方意义下，线性回归的结果就是条件期望。将 X 中心化后做回归
$$X^{(1)}-{\mu }^{(1)}={\beta }^{\prime }\left(X^{(2)}-{\mu }^{(2)}\right)+\epsilon$$

那么 ${\beta }^{\prime }\left(x^{(2)}-{\mu }^{(2)}\right)$ 就是 $X^{(1)}-{\mu }^{(1)}$ 的条件期望。现在假设对于每个变量，都有 $n$ 个观测数据，并将回归形式改写为 $Z_t={\beta }^{\prime }{R}_t+\epsilon$ ，那么利用最小二乘估计可以得到参数的估计量为 $\beta ={\left(R^{\prime }R\right)}^{-1}{R}^{\prime }Z$ 。考虑当 $n$ 充分大的情况下， ${\left(R^{\prime }R\right)}^{-1}$ 对应了 ${\Sigma }_{22}^{-1}，R^{\prime }Z$ 对应了 ${\Sigma }_{21}$ 进而对 $\beta$ 求转置后得到
$$X^{(1)}={\mu }^{(1)}+{\Sigma }_{12}{\Sigma }_{22}^{-1}\left(X^{(2)}-{\mu }^{(2)}\right)+\epsilon$$

因此条件期望就是$${\mu }_{1\cdot 2}={\mu }^{(1)}+{\Sigma }_{12}{\Sigma }_{22}^{-1}\left(x^{(2)}-{\mu }^{(2)}\right)$$

下面考虑条件方差的计算。做回归后得到的误差项 $\epsilon$ 是从 $X^{(1)}$ 中剔除了 $X^{(2)}$ 对其的影响，那么条件方差就应该等于误差项的方差，即
$$\begin{array}{rl}{\Sigma }_{1\cdot 2}& =\mathrm{Var}\epsilon =\mathrm{Var}\left(X^{(1)}-{\mu }^{(1)}\right)-\mathrm{Var}\left[{\Sigma }_{12}{\Sigma }_{22}^{-1}\left(X^{(2)}-{\mu }^{(2)}\right)\right]\\ & ={\Sigma }_{11}-{\Sigma }_{12}{\Sigma }_{22}^{-1}{\Sigma }_{22}{\left({\Sigma }_{12}{\Sigma }_{22}^{-1}\right)}^{\prime }={\Sigma }_{11}-{\Sigma }_{12}{\Sigma }_{22}^{-1}{\Sigma }_{21}\end{array}$$

由此可以自然地得到下面的推论：

$X^{(2)}与X^{(1)}-{\Sigma }_{12}{\Sigma }_{22}^{-1}{X}^{(2)}$ 相互独立
$X^{(1)}与X^{(2)}-{\Sigma }_{21}{\Sigma }_{11}^{-1}{X}^{(1)}$ 相互独立
$X^{(2)}\mid X^{(1)}\sim N_{p-r}\left({\mu }_{2\cdot 1},{\Sigma }_{2\cdot 1}\right)$, 其中
$$\begin{array}{c}{\mu }_{2\cdot 1}={\mu }^{(2)}+{\Sigma }_{21}{\Sigma }_{11}^{-1}\left(x^{(1)}-{\mu }^{(1)}\right)\\ {\Sigma }_{2\cdot 1}={\Sigma }_{22}-{\Sigma }_{21}{\Sigma }_{11}^{-1}{\Sigma }_{12}\end{array}$$

问：如果是三个子向量，给定其中两个，求另一个的条件分布呢？
答：把给定的两个看做一个子向量就可以。

条件数字特征

就是刚刚推导的东西的定义

（1）条件期望(Conditional Expectation)，回归系数(regression coefficient)，偏相关系数(Partial correlation coefficient)
设$$X=\left[\begin{array}{c}{X}^{(1)}\\ X^{(2)}\end{array}\right]\sim N_p\left(\left[\begin{array}{c}{\mu }^{(1)}\\ {\mu }^{(2)}\end{array}\right],\left[\begin{array}{cc}{\Sigma }_{11}& {\Sigma }_{12}\\ {\Sigma }_{21}& {\Sigma }_{22}\end{array}\right]\right)$$

根据定理2有 $\left(X^{(1)}\mid X^{(2)}=x^{(2)}\right)\sim N_r\left({\mu }_{1\cdot 2},{\Sigma }_{1\cdot 2}\right)$，我们把
$${\mu }_{1\cdot 2}={\mu }^{(1)}+{\Sigma }_{12}{\Sigma }_{22}^{-1}\left(x^{(2)}-{\mu }^{(2)}\right)$$

称为条件期望(Conditional Expectation)，记作 $\mathrm{E}\left(X^{(1)}\mid X^{(2)}=x^{(2)}\right)$ ；把 ${\Sigma }_{12}{\Sigma }_{22}^{-1}\stackrel{\text{def}}{=}B$ 称为回归系数.

为了定义偏回归系数，将条件方差矩阵的元素具体表示为
$${\Sigma }_{1\cdot 2}={\left({\sigma }_{ij}\right)}_{r\times r}(i,j=1,\cdots ,r)$$

称$${\rho }_{ij\cdot r+1,\cdots ,p}=\frac{{\sigma }_{ij}}{\sqrt{{\sigma }_{ii}}\sqrt{{\sigma }_{jj}}}$$ 为偏相关系数，即为 $X^{(2)}={\left(X_{r+1},\cdots ,X_p\right)}^{\prime }$ 给定的条件下， $X_i,X_j$ 的相关系数.

（2）全相关系数（了解）
设 $Z=\left[\begin{array}{l}X\\ Y\end{array}\right]\begin{array}{l}p\\ 1\end{array}\sim N_{p+1}\left(\left[\begin{array}{c}{\mu }_X\\ {\mu }_y\end{array}\right],\left[\begin{array}{cc}{\Sigma }_{XX}& {\Sigma }_{Xy}\\ {\Sigma }_{yX}& {\sigma }_{yy}\end{array}\right]\right)$，则称
$$R={\left(\frac{{\sum }_{yX}{\Sigma }_{XX}^{-1}{\Sigma }_{Xy}}{{\sigma }_{yy}}\right)}^{1/2}$$

为 $Y$ 与 $X={\left(X_1,\cdots ,X_p\right)}^{\prime }$ 的全相关系数.

（3）最佳预测
记 $X^{(1)}=Y,g\left(x^{(2)}\right)=E\left(Y\mid X^{(2)}=x^{(2)}\right)$ ，则对任意函数 $\varphi (\cdot )$ ，可以证明
$$E\left[{\left(Y-g\left(x^{(2)}\right)\right)}^2\right]\le E\left[{\left(Y-\varphi \left(x^{(2)}\right)\right)}^2\right]$$

也就是在均方准则下，条件期望是最优预测，证明方法就是加一项减一项，往证交叉项为0.

6. 高斯过程

6.1 简介

高斯过程(Gaussian process, GP) 是一个概率统计学上的概念，更确切的说应该是随机过程(Stochastic process)中一个特殊例子。
在高斯过程中，连续输入空间中每个点都是与一个正态分布的随机变量相关联。此外，这些随机变量的每个有限集合都有一个多元正态分布。高斯过程的分布是所有那些（无限多个）随机变量的联合分布，正因如此，它是连续域（例如时间或空间）的分布。

【定义】 对于一个连续域 $T$ （假设他是一个时间轴），如果我们在连续域上任选 $n$ 个时刻： $t_1,t_2,t_3,...,t_n\in T$ ，使得获得的一个 $n$ 维向量 $\{{\xi }_1,{\xi }_2,{\xi }_3,...,{\xi }_n\}$ 都满足其是一个 $n$ 维高斯分布，那么这个 $\{{\xi }_t\}$ 就是一个高斯过程。

GP可以被mean和covariance function共同唯一决定其表达式，具体的，${\xi }_t\sim GP(m(t),k(t,s))$。因为我们知道一个高斯分布可以被mean和variance共同唯一决定，一个多元高斯分布可以对mean vector和covariance matrix共同唯一决定。mean需要描述每一个时间点 t 上的均值，但是这个时候就不能用向量了，因为是在连续域上的，维数是无限的，因此就应该定义成一个关于时刻 t 的函数： m(t) 。covariance function被称为核函数kernel，原因就是它捕捉了不同输入点之间的关系，并且反映在了之后样本的位置上。这样的话，就可以做到，利用点与点之间关系，以从输入的训练数据预测未知点的值。比如径向基函数 RBF：
$$k(s,t)={\sigma }^{2}exp(-\frac{||s-t|{|}^2}{2l^2})$$

这里 $\sigma$ 和 $l$ 是径向基函数的超参数。$s$ 和 $t$ 表示高斯过程连续域上的两个不同的时间点， $||s-t|{|}^2$ 是一个二范式，简单点说就是 $s$ 和 $t$ 之间的距离，径向基函数输出的是一个标量，他代表的就是 $s$ 和 $t$ 两个时间点各自所代表的高斯分布之间的协方差值，很明显径向基函数是一个关于 $s$，$t$ 距离负相关的函数，两个点距离越大，两个分布之间的协方差值越小，即相关性越小，反之越靠近的两个时间点对应的分布其协方差值就越大。

import numpy as np
def gaussian_kernel(x1, x2, l=1.0, sigma_f=1.0):
    m, n = x1.shape[0], x2.shape[0]
    dist_matrix = np.zeros((m, n), dtype=float)
    for i in range(m):
        for j in range(n):
            dist_matrix[i][j] = np.sum((x1[i] - x2[j]) ** 2)
    return sigma_f ** 2 * np.exp(- 0.5 / l ** 2 * dist_matrix)

train_X = np.array([1, 3, 7, 9]).reshape(-1, 1)#转换为4*1矩阵形式
print(gaussian_kernel(train_X, train_X)) #4*4矩阵，当 i=j 时，就是自身的方差

6.2 高斯过程回归

我们知道，高斯分布有一个很好的特性，那就是高斯分布的联合概率、边缘概率、条件概率仍然是满足高斯分布的，假设：
$n$ 维的随机变量满足高斯分布： $x\sim N(\mu ,{\Sigma }_{n\times n})$
那么如果我们把这个 $n$维的随机变量分成两部分： $p$ 维的 $x_a$ 和 $q$ 维的 $x_b$ ，满足 $n=q+p$ ，那么按照均值向量 $\mu$ 和协方差矩阵 $\Sigma$ 的分块规则，就可以写成：
$$x={\left[\begin{array}{c}{x}_a\\ x_b\end{array}\right]}_{p+q}\mu ={\left[\begin{array}{c}{\mu }_a\\ {\mu }_b\end{array}\right]}_{p+q}\Sigma =\left[\begin{array}{cc}{\Sigma }_{aa}& {\Sigma }_{ab}\\ {\Sigma }_{ba}& {\Sigma }_{bb}\end{array}\right]$$

那么依据高斯分布的性质，我们知道下列条件分布依然是一个高维的高斯分布：
$$\begin{gathered} x_b|x_a\sim N({\mu }_{b|a},{\Sigma }_{b|a}) \\ {\mu }_{b|a}={\Sigma }_{ba}{\Sigma }_{aa}^{-1}(x_a-{\mu }_a)+{\mu }_b \\ {\Sigma }_{b|a}={\Sigma }_{bb}-{\Sigma }_{ba}{\Sigma }_{aa}^{-1}{\Sigma }_{ab} \end{gathered}$$

也就是说，设置了高斯过程的先验参数，一旦我们拿到一些观测值，那么就可以对高斯过程的均值函数和核函数进行修正，得到一个修正后的后验高斯过程，而更新后验参数的信息就来自于观测值。

将高斯过程对比高维高斯分布，我们把均值向量替换成均值函数，把协方差矩阵替换成核函数，就能够得到高斯过程基于观测值的后验过程的参数表达式：
我们的一组观测值，他们的时刻对应一个向量 $X$ ，那么对应的值时另一个同纬度的向量的 $Y$ ，假设有4组观测值，那就是 { ( X [ 1 ] , Y [ 1 ] ) , ( ( X [ 2 ]