Inverse Depth Parametrization
Inverse Depth Parametrization
-
- 1.论文
- 2.逆深度参数化
- 3.测量模型
1.论文
. 特征深度估计中,像太阳和云一样的特征和其他非常远的东西将具有inf的距离估计。这可能会导致很多问题,为了解决它,估计距离的倒数,所有inf都变为零,这往往会导致更少的问题。
论文1:Unified Inverse Depth Parametrization for Monocular SLAM.(Robotics: Science and Systems 2006;Philadelphia, PA, USA, August 16-19, 2006); 论文2:SLAM_ Inverse Depth Parametrization for Monocular SALM.(IEEE TRANSACTIONS ON ROBOTICS, VOL. 24, NO. 5, OCTOBER 2008).
论文2对远点采用一种逆深度参数化的方式,并且得到经验性数据,一般不超过基线距40倍的深度可以被有效参数化,并用来计算相机旋转,位移和尺度;超过40倍baseline的为远点,可以提供旋转信息,但是位移和尺度信息比较弱,其需要在多个视图的支持下进行三角化。
2.逆深度参数化
We show that once the depth estimate of a feature is sufficiently accurate, its representation can safely be converted to the Euclidean XYZ form, and propose a linearity index that allows automatic detection and conversion to maintain maximum efficiency—only low parallax features need be maintained in inverse depth form for long periods.
当特征的深度估计足够准确,其表示可以转换为欧几里德XYZ形式。
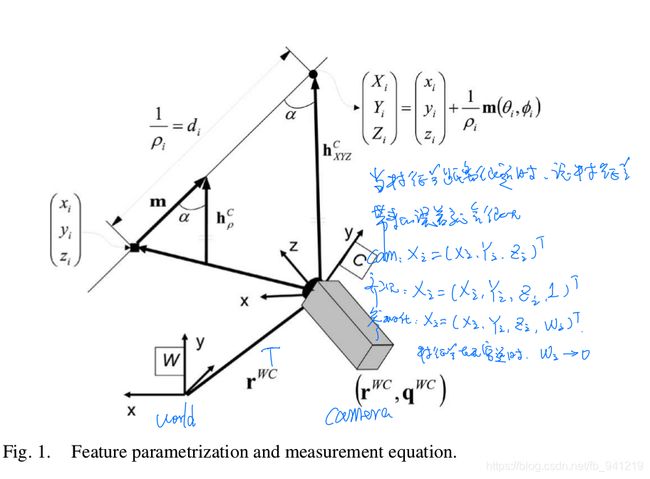

详细推导没看,见论文。 有两个疑问:
1.普通的单目相机或RGB-D相机如何求取 θ i \theta _i θi与 ϕ i \phi _i ϕi?
2.只是将 ρ i { \rho }_{ i } ρi 进行优化后,如何结合优化后的 ρ i { \rho }_{ i } ρi 与未优化的 x i = ( X i , Y i , Z i ) T x_i=(X_i,Y_i,Z_i)^T xi=(Xi,Yi,Zi)T 恢复得到优化后的 x i = ( X i , Y i , Z i ) T x_i=(X_i,Y_i,Z_i)^T xi=(Xi,Yi,Zi)T ?
更.
坐标系回顾

. 逆深度参数是一个六维变量,假设目标上第i个特征点的逆深度参数表示为: y i w = ( x i , y i , z i , θ i , ϕ i , ρ i ) T {y_i}^w=(x_i, y_i, z_i,\theta _i,\phi _i,{ \rho }_{ i })^T yiw=(xi,yi,zi,θi,ϕi,ρi)T ( x i , y i , z i ) T (x_i, y_i, z_i)^T (xi,yi,zi)T表示视觉相机在世界坐标系下的位置, θ i \theta _i θi与 ϕ i \phi _i ϕi分别表示目标特征 P i P_i Pi在世界坐标下,视觉相机光心与特征点连线相对于光轴方向的方位角和高低角。该点在欧氏空间中的表示向量为: x i w = ( X i , Y i , Z i ) T {x_i}^w=(X_i, Y_i, Z_i)^T xiw=(Xi,Yi,Zi)T

. 在第一次检测到新特征时,视觉相机在世界坐标系下的坐标为 ( x i , y i , z i ) T (x_i, y_i, z_i)^T (xi,yi,zi)T,目标点 P i P_i Pi在图像坐标系下的坐标为 ( u , v , 1 ) T (u,v, 1)^T (u,v,1)T,由小孔成像模型得,其在世界坐标系下的表达式为: p w = ( p x w , p y w , p z w ) T = R W C K ( u , v , 1 ) T p^w=({p_x}^w,{p_y}^w,{p_z}^w)^T=R^{WC} K(u, v, 1)^T pw=(pxw,pyw,pzw)T=RWCK(u,v,1)T 其中, R W C R^{WC} RWC表示从视觉相机坐标系到世界坐标系的旋转矩阵,K表示相机内参。所以,目标点 P i P_i Pi在世界坐标系下的方位角和高低角分别为:
θ i = a r c t a n ( p x w / p z w ) \theta _i=arctan({ { p_{ x } }^{ w } }/{ { p_{ z } }^{ w } }) θi=arctan(pxw/pzw) ϕ i = a r c t a n ( − p y w / ( p x w ) 2 + ( p z w ) 2 ) \phi _{ i }=arctan(-{ { p_{ y } }^{ w } }/{ \sqrt { { { (p_{ x } }^{ w })^{ 2 } }+{ (p_{ z } }^{ w })^{ 2 } } }) ϕi=arctan(−pyw/(pxw)2+(pzw)2) 目标点 P i P_i Pi的深度为 d = 1 / ρ d=1/ρ d=1/ρ,则该点在世界坐标系下的欧氏坐标为(m为以 θ i θ_i θi和 ϕ i \phi_i ϕi表示的单位方向向量):

3.测量模型
