C++作业:向量类和矩阵类的操作符重载
文章目录
- 向量类和矩阵类的操作符重载
-
- 题目要求
- 思考过程
- 代码
- 结果展示
- 总结
向量类和矩阵类的操作符重载
题目要求
题目描述
实现一个向量类,一个矩阵类。在这两个类中,分别重载 “+, -, *(数乘,矩阵乘) ” 基本运算以及 “==,!=,-(负号), =(赋值)" 操作符,以实现向量、矩阵的基本运算。
要求:
- 除了重载相应的操作符,也需要实现一个类的一些基本的方法(接口),比如构造、析构、拷贝构造等。
- 可以使用C++标准模板库(STL)里面的vector类,也可以使用你前一次作业实现的动态数组作为你这次所要实现的向量类的基础。
提示:
- 此次会提供一份测试代码(非线上测试代码)
- 该测试用例中涉及的Vecto自行设计,逐渐熟悉并掌握类接口设计能力
- 建议可以先注释掉全部或大部分测试代码,从而以免在一开始因代码仅完成很少部分,产生太多编译错误
- 仅通过测试代码分析类的职责,开发完成后,放开测试代码
- 测试不通过,再考虑职责分析是否有误解
- 建议思考的方式为“我应该为Vector提供什么接口,这些接口应当完成什么功能以满足他们的职责”为出发点,实现后通过测试用例验证
- 而非“我应该为Vector提供什么接口,以能通过测试代码”为出发点,通不过一句,改一个函数,通过一句,就转移到下一个函数的方式
- 前者以对象为中心,考虑职责,在思考过程和实现过程中,类独立设计并实现,最终通过交互完成功能,类设计和实现的过程和测试代码的顺序无关,
- 仅与自身从测试代码中分析并融合出的职责需求有关
- 后者以过程为中心,考虑功能,思考过程和实现的过程中,类在不断的“测试过程”中运行,以测试代码运行的顺序增加功能
输入
注:由于这次作业不需要提交main()函数,因此输入部分不需要过多关注
第一行n为整数,表示操作的个数
第二行的是对数组进行相应操作的代码(整数编码)序列,以空格分隔。
第三行是m 个数据(m操作序列所需的操作数决定)。
注:由于这次作业不需要提交main()函数,因此输入部分不需要过多关注

思考过程
- 向量类使用了
vector容器 - 矩阵类使用线性的内存,顺序存放
assert()的调用使得调试更加方便
代码
/*向量类和矩阵类的重载运算
* by——keli
*2020.12.12
*/
#include Data;
static Vector INVALID_VECTOR;
public:
//无参数构造函数
Vector();
//长度和一个数组为参数的构造函数
Vector(int length, const double data[]);
//参数为长度和一个double数的构造函数
Vector(int length, const double data);
//析构函数
~Vector();
public:
//返回向量元素个数
int size() const;
//重载[]
double operator[](int index) const;
//重载+
Vector operator+(const Vector& temp) const;
//重载-
Vector operator-(const Vector& temp) const;
//重载*
Vector operator*(const double a) const;
//重载==
bool operator==(const Vector& temp) const;
//重载!=
bool operator!=(const Vector& temp) const;
//重载负号
Vector operator-() const;
//重载=double
Vector operator=(const double element);
//重载+double,每个元素都加一个数
Vector operator+(const double element)const;
//重载-double,每个元素都减一个数
Vector operator-(const double element);
private:
//重载<<
friend std::ostream& operator<<(std::ostream& os, const Vector& vector);
private:
//数据,向量p
vector<double>p;
};
Vector::Vector()
{
p.clear();
}
Vector::Vector(int length, const double data[])
{
//这里的初始化和容器插入不同,必须先把容器归零
p.clear();
for (int i = 0; i < length; i++)
{//把data[]的数据放入vector
p.push_back(data[i]);
}
}
Vector::Vector(int length, const double data)
{
p.clear();
for (int i = 0; i < length; i++)
{
p.push_back(data);
}//length个数据初始为data
}
Vector::~Vector()
{
p.clear();//清理内存
}
int Vector::size()const
{
//vector内置函数size,返回容器元素个数
return p.size();
}
double Vector::operator[](int index)const
{
//随机访问容器元素
return p.at(index);
}
Vector Vector::operator+(const Vector& temp)const
{
if (p.size() != temp.p.size())//容量不相等时
{
return Vector::INVALID_VECTOR;//返回非法向量
}
Vector sum;//和向量
for (int i = 0; i < p.size(); i++)
{
sum.p.push_back(p.at(i) + temp.p.at(i));
}
return sum;
}
Vector Vector::operator-(const Vector& temp)const
{
if (p.size() != temp.p.size())//容量不相等时
{
return Vector::INVALID_VECTOR;//返回非法向量
}
Vector difference;//差向量
for (int i = 0; i < p.size(); i++)
{
difference.p.push_back(p.at(i) - temp.p.at(i));
}
return difference;
}
Vector Vector::operator*(const double a)const
{
Vector product;//积向量
for (int i = 0; i < p.size(); i++)
{
product.p.push_back(p.at(i)*a);
}
return product;
}
bool Vector::operator==(const Vector& temp)const
{
return (this->p == temp.p);
}
bool Vector::operator!=(const Vector& temp)const
{
return (!(this->p == temp.p));
}
Vector Vector::operator-()const
{
Vector opposite;
for (int i = 0; i < p.size(); i++)
{
opposite.p.push_back(p.at(i)*(-1.0));
}
return opposite;
}
Vector Vector::operator=(const double element)
{//把值改为3,长度不变
int _len = p.size();
p.clear();//容器重置
p.resize(_len, element);
return *this;
}
Vector Vector::operator+(const double element)const
{
Vector dst;
for (int i = 0; i < p.size(); i++)
{
dst.p.push_back(p[i] + element);
}
return dst;
}
Vector Vector::operator-(const double element)
{
Vector dst;
for (vector<double>::iterator it = p.begin(); it < p.end(); ++it)
{
dst.p.push_back(*it - element);
}
return dst;
}
std::ostream& operator<<(std::ostream& os, const Vector& vector)
{
for (int i = 0; i < vector.p.size(); i++)
os << vector.p.at(i) << " ";
os << std::endl;
return os;
}
//把无效向量设置为0向量
Vector Vector::INVALID_VECTOR(0, 1.0);
/****************下面是矩阵类******************************************/
class Matrix
{
public:
/// 定义类型便于其他代码使用
// typedef std::vector Data;
/// 定义非法矩阵,这里用0 * 0矩阵表示,也可在Matrix中添加一个特殊标志位
static Matrix INVALID_MATRIX;
public:
// Matrix类构造函数.
/// 默认构造函数要加,否则vector无法resize
Matrix();
//用向量初始化矩阵的构造函数
Matrix(const Vector& rsh);
//初始化行、列的构造函数
Matrix(int row, int col);
//行列向量,三参数构造函数
Matrix(int row, int col, const double data[]);
//行列和一个双精度数的构造函数
Matrix(int row, int col, const double data);
//拷贝构造函数
Matrix(const Matrix& rsh);
// Matrix类析构函数
~Matrix()
{
delete[] p;
row = 0;
column = 0;
}
//返回行数
int rows()const;
//返回列数
int cols()const;
//矩阵转置
Matrix trans()const;
public:
//重载矩阵的数乘
Matrix operator*(const double element)const;
//重载[],返回值是指针,本质上为了实现matrix[][]的访问
double* operator[](const int row)const;
//重载==
bool operator==(const Matrix& rsh)const;
//重载!=
bool operator!=(const Matrix& rsh)const;
//重载+
Matrix operator+(const Matrix& rsh)const;
//重载-
Matrix operator-(const Matrix& rsh)const;
//重载相反数运算
Matrix operator-(void)const;
//重载矩阵乘法
Matrix operator*(const Matrix& rsh)const;
private:
// Matrix类私有实现方法
int row; // 行
int column;//列
//访问时p[i+j*column]就相当于二维数组里的p[i][j]
double * p;//一维向量来存储矩阵
private:
/// 所有成员变量应设为私有
/// operator<<需加友元声明,否则无法打印
friend std::ostream& operator<<(std::ostream& out, const Matrix& rsh);
}; // class Matrix类定义结束.
Matrix::Matrix()
{
p = NULL;
row = 0;
column = 0;
}
Matrix::Matrix(const Vector& rsh)
{//向量相当于行数为1的矩阵
row = 1;
column = rsh.size();
p = new double[row*column];
for (int j = 0; j < row * column; j++)
{
p[j] = rsh[j];
}
}
Matrix::Matrix(int row, int col)
{
this->row = row;
this->column = col;
p=new double[row * column];
}
Matrix::Matrix(int row, int col, const double data[])
{
this->row = row;
this->column = col;
p = new double[row * column];
for (int i = 0; i < row*column; i++)
{
p[i] = data[i];
}
}
Matrix::Matrix(int row, int col, const double data)
{
this->row = row;
this->column = col;
p = new double[row * column];
for (int i = 0; i < row * column; i++)
{
p[i] = data;
}
}
Matrix::Matrix(const Matrix& rsh)
{
row = rsh.row;
column = rsh.column;
p = new double[row * column];
for (int i = 0; i < row * column; i++)
{
p[i] = rsh.p[i];
}
}
int Matrix::rows()const
{
return row;
}
int Matrix::cols()const
{
return column;
}
Matrix Matrix::operator*(const double element) const
{
Matrix dst(*this);
for (int i = 0; i < row * column; i++)
dst.p[i] = p[i] * element;
return dst;
}
double* Matrix::operator[](const int row)const
{
return p + row * this->column;
}
bool Matrix::operator==(const Matrix& rsh) const
{
if (row != rsh.row || column != rsh.column)
return false;
for (int i = 0; i < row * column; i++)
{
if (rsh.p[i] != p[i])
return false;
}
return true;
}
bool Matrix::operator!=(const Matrix& rsh) const
{
return !(*this == rsh);
}
Matrix Matrix::operator+(const Matrix& rsh) const
{
//矩阵行数列数不一样时返回非法矩阵
if (row != rsh.rows() || column != rsh.cols())
return INVALID_MATRIX;
Matrix dst(*this);
for (int i = 0; i < dst.cols() * dst.rows(); i++)
{
dst.p[i] = p[i] + rsh.p[i];
}
return dst;
}
Matrix Matrix::operator-(const Matrix& rsh) const
{
//矩阵行数列数不一样时返回非法矩阵
if (row != rsh.rows() || column != rsh.cols())
return INVALID_MATRIX;
Matrix dst(*this);
for (int i = 0; i < dst.cols() * dst.rows(); i++)
{
dst.p[i] = p[i] - rsh.p[i];
}
return dst;
}
Matrix Matrix::operator-(void)const
{
Matrix dst(*this);
for (int i = 0; i < dst.cols() * dst.rows(); i++)
{
dst.p[i] = -p[i];
}
return dst;
}
Matrix Matrix::operator*(const Matrix& rsh)const
{
if (this->cols() != rsh.rows())//第一个矩阵的列数与第二个矩阵的行数不相等
{//返回非法矩阵
return Matrix::INVALID_MATRIX;
}
Matrix dst(this->rows(), rsh.cols());
for (int i = 0; i < row; i++)
{
for (int j = 0; j < dst.column; j++)
{
double temp = 0;
for (int k = 0; k <column; k++)
{
temp += (*this)[i][k] * rsh[k][j];
}
dst[i][j]= temp;
}
}
return dst;
}
Matrix Matrix::trans()const
{
Matrix dst(this->cols(), this->rows());
for (int i = 0; i <rows(); i++)
{
for (int j = 0; j <cols(); j++)
{
dst[j][i] = (*this)[i][j];
}
}
return dst;
}
//非法矩阵设置为0
Matrix Matrix::INVALID_MATRIX(0, 0);
// 定义Matrix流输出操作
std::ostream& operator<<(std::ostream& out, const Matrix& rsh)
{
out << "输出矩阵" << endl;
for (int i = 0; i < rsh.row; i++)
{
for (int j = 0; j < rsh.column; j++)
{
out << rsh.p[j + i * rsh.column] << " ";
}
out << endl;
}
return out;
}
// 提供的测试代码
// 该测试用例中涉及的Vector及Matrix自行设计,逐渐熟悉并掌握类接口设计能力
// 建议可以先注释掉全部或大部分测试代码,从而以免在一开始因代码仅完成很少部分,产生太多编译错误
// 仅通过测试代码分析类的职责,开发完成后,放开测试代码
// 测试不通过,在考虑职责分析是否有误解
// 建议思考的方式为“我应该为Vector和Matrix提供什么接口,这些接口应当完成什么功能以满足他们的职责”为出发点,实现后通过测试用例验证
// 而非“我应该为Vector和Matrix提供什么接口,以能通过测试代码”为出发点,通不过一句,改一个函数,通过一句,就转移到下一个函数的方式
// 前者以对象为中心,考虑职责,在思考过程和实现过程中,类独立设计并实现,最终通过交互完成功能,类设计和实现的过程和测试代码的顺序无关,
// 仅与自身从测试代码中分析并融合出的职责需求有关
// 后者以过程为中心,考虑功能,思考过程和实现的过程中,类在不断的“测试过程”中运行,以测试代码运行的顺序增加功能
int main(int argc, char *argv[])
{
// 通过传递元素素组初始化向量,最终将得到3个元素
double data1[] = {3.4, 4.4, 6.0};
Vector v(sizeof(data1) / sizeof(double), data1);
// 确保完备的初始化向量
assert(v.size() == sizeof(data1) / sizeof(double));
for (int idx = 0; idx < sizeof(data1) / sizeof(double); ++idx)
{
assert(v[idx] == data1[idx]);
}
// v的值应等于自身,且不会不等于自身
assert(v == v);
assert(!(v != v));
// v + v按元素分别求和的结果,相当于每个元素直接与2相乘
assert(v + v == v * 2);
// v - v按元素分别求和的结果,相当于v加上v的相反数
assert(v - v == v + (-v));
// v = 3的结果使向量的每个元素都变为3,因此等于直接初始化一个只有三个元素,且初始值为3的向量
assert((v = 3) == Vector(sizeof(data1) / sizeof(double), 3));
// v + 3的结果使向量的每个元素都加上3,因此等于直接初始化一个只有三个元素,且初始值为6的向量
// 而 v - 3则直接初始化一个只有三个元素,且初始值为0的向量
assert(v + 3 == Vector(sizeof(data1) / sizeof(double), 6));
assert(v - 3 == Vector(sizeof(data1) / sizeof(double), 0.0));
// 另行定义一个有十个元素,且每个元素值为5的向量
Vector v2(10, 5);
// 确保其正确初始化
assert(v2.size() == 10);
for (int idx = 0; idx < v2.size(); ++idx)
{
assert(v2[idx] == 5);
}
// 两个元素个数不相等的向量相加,其结果为【无效向量】
assert(v + v2 == Vector::INVALID_VECTOR);
//
// 通过传递元素素组初始化矩阵,3( 行) X 2(列) 矩阵为:
// 1 1
// 1 1
// 1 1
double data2[] = {1, 1, 1, 1, 1, 1};
Matrix m1(3, 2, data2);
// m4等于m1乘以标量2,因此按元素分别求乘积,得到3( 行) X 2(列) 矩阵,为:
// 2 2
// 2 2
// 2 2
Matrix m4 = m1 * 2;
// 确保m1初始化正确,且与标量乘积正确
assert(m4.rows() == 3);
assert(m4.cols() == 2);
for (int r = 0; r < 2; ++r)
{
for (int c = 0; c < 2; ++c)
{
assert(m4[r][c] == 2);
}
}
// 以同样的数组初始化矩阵,但如果行数、列数不同,获得的矩阵也不同
Matrix m2(6, 1, data2);
Matrix m3(3, 2, data2);
// 因此m1与m2同样有6个1,但行列不同,因此不相等
assert(m1 != m2);
// 只有m3这样的行列相同,元素相同,才应相等
assert(m1 == m3);
// 同样的结果可以通过直接初始化每个元素为一个相同的数值得到
assert(m1 == Matrix(3, 2, 1));
// m1相加之后,应得到一个3行2列,元素全为2的矩阵
assert(m1 + m1 == Matrix(3, 2, 2));
// 但如果矩阵行列不同,无法直接相加,只能得到非法矩阵
assert(m1 + m2 == Matrix::INVALID_MATRIX);
// 同样,减法按元素相减,相当于加上相反数
assert(m1 - m1 == m1 + (-m1));
// 相反数的结果应正确
assert(-m1 == Matrix(3, 2, -1));
// 在乘法中,如果矩阵行列不满足条件,只能得到非法矩阵
assert(m1 * m1 == Matrix::INVALID_MATRIX);
// 满足乘法条件,m1与其转置矩阵的乘积((3 X 2) X (2 X 3))为3行3列元素为2矩阵
assert(m1 * m1.trans() == Matrix(3, 3, 2));
// 满足乘法条件,m1转置矩阵与m1的乘积((2 X 3) X (3 X 2))为2行2列元素为3矩阵
assert(m1.trans() * m1 == Matrix(2, 2, 3));
//cout << v;
cout << m1;
cout << Matrix(v);
cout << (Matrix(v) * m1);
//向量可转化为矩阵与矩阵相乘,同样要满足矩阵乘法条件,由于v相当于1X3矩阵,元素为3,因此结果为1X2矩阵,元素为9
assert(Matrix(v) * m1 == Matrix(1, 2, 9));
// 改变顺序后也可通过转置获得另一个乘积,因此结果为2X1矩阵,元素为9,即相当于上面一个结果的转置
assert(m1.trans() * Matrix(v).trans() == Matrix(2, 1, 9));
return 0;
}
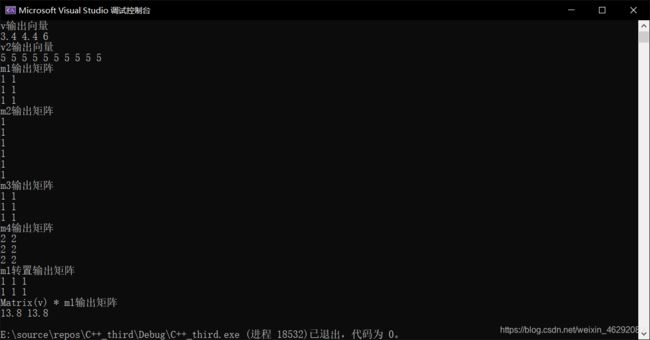
结果展示
- 本次实验实际上没有输入和输出
- 为了展示结果,写了一个
show()函数,再最后进行调用
void show()
{
// 通过传递元素素组初始化向量,最终将得到3个元素
double data1[] = { 3.4, 4.4, 6.0 };
Vector v(sizeof(data1) / sizeof(double), data1);
cout << "v";
cout << v;
// 另行定义一个有十个元素,且每个元素值为5的向量
Vector v2(10, 5);
cout << "v2";
cout << v2;
double data2[] = { 1, 1, 1, 1, 1, 1 };
Matrix m1(3, 2, data2);
Matrix m4 = m1 * 2;
Matrix m2(6, 1, data2);
Matrix m3(3, 2, data2);
cout << "m1" << m1;
cout << "m2" << m2;
cout << "m3" << m3;
cout << "m4" << m4;
cout << "m1转置" << m1.trans();
cout << "Matrix(v) * m1" << Matrix(v) * m1;
}
总结
- 再次复习了
vector容器的基本用法 - 复习了C++内存的申请和使用
- 进一步掌握了程序调试方法,
assert()函数的使用