状态压缩与位运算入门

引子

某类问题包含很多的信息，每一个信息都需要一个数组来存储。
例如：有一道题是关于n扇门的状态的问题，有5个门，1代表开，0代表关。那么用数组描述a[1]—a[5]：分别为0 1 1 0 1 就代表 关 开 开 关 开，如果n是一个很大的数10^8，数组往往开的太大了！
所以呢，为了避免空间开太大，也为了方便程序描述状态，可以把这个状态压缩成一个十进制的数字13来代替，
因为（13）=01101

for (int i=0;i<2^5;i++)  {
	...;
}
//一个循环穷举了00000-11111五扇门的所有状态。

既有利于信息和状态的描述，程序编写，也有利于节约空间。
状态压缩：将n个数的状态压成一个二进制数，把一个状态压缩成数字里的一位，要处理题意里的状态之间的相互关系，必须使用位运算。
附录

• C++运算符的优先级

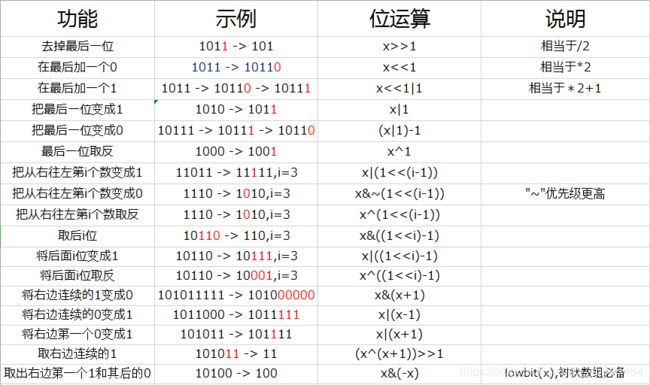
位运算

位运算运算符

右边对齐，左边不足补0，按位运算

1、 & (与) ：

a & b 只有 a b 都等于 1 ，a & b == 1

Example： 10101 & 01001 = 00001

特征：

• 任意一位&1 为原数

2、| (或)：

a | b 只要 a 与 b 有一个是1 ，a | b == 1

E： 10101 | 1001 = 11101

特征

• 任意一位 | 1 为1
• 任意一位 | 0 为原数

3、^ (异或):

a ^ b 只要 a b 不相同 ，a ^ b == 1

E：10101 ^ 1001 = 11100

特征

• 任意一位 ^ 1 取反
• 任意一位 ^ 0 为原数

状压DP（位运算）的常用操作

（图片原创）

状压经典例题

一类问题

ybt 1593：牧场的安排
农夫约翰的土地由M*N个小方格组成，现在他要在土地里种植玉米。非常遗憾，部分土地是不育的，无法种植。
而且，相邻的土地不能同时种植玉米，也就是说种植玉米的所有方格之间都不会有公共边缘。
现在给定土地的大小，请你求出共有多少种种植方法。
土地上什么都不种也算一种方法。数据范围 （1≤M,N≤12）
输入格式
第1行包含两个整数M和N。
第2…M+1行：每行包含N个整数0或1，用来描述整个土地的状况，1表示该块土地肥沃，0表示该块土地不育。
输出格式
输出总种植方案。
输入样例：

2 3
1 1 1
0 1 0

输出样例：

9

思路
状态描述
每一行的种植情况（状态）可以描述成一个二进制的数 j：10010101 （0<=j<=2ⁿ-1）
共有m行
定义状态：$f[i][j]$表示在第i行状态是j的方案数
初始边界条件：
第一行所有可行状态j：$f[1][j]=1$;
不可行方案：$f[1][j]=0$;
目标状态：
最后一行m行所有可行方案的和$f[m][j]$
状态转移
f[i][j]表示在第i行状态是j的方案数
以行作为阶段： i从1到m，从上往下一行一行遍历, 上一行i-1有一个合法状态k（ $f[i-1][k]$ ）如果和 j 没有冲突：
$f[i][j]+=f[i-1][k]$

预处理是很重要的技巧
Code:

#include
#include
#define LL long long
using namespace std;
//有些土地相当的贫瘠，不能用来放牧。
//没有哪两块草地有公共边。
//1≤N,M≤12。
const LL MOD=1e8;
const int N=12+3;
const int S=(1<<N)+5;
//1 表示这块土地足够肥沃，0 则表示这块地上不适合种草。
int n,m;
int mp[N];
int a[N][S]; //第N行上的预处理方案 
LL f[N][S];
void Init() //输入和预处理 
{
	int i,j,k;
	int x,y,z;
	cin>>n>>m;
	for(i=1;i<=n;i++) {
		for(j=1;j<=m;j++) {
			cin>>x;
			x=!x;
			mp[i]=(mp[i]<<1)|x;
		}
		for(k=0;k<=(1<<m)-1;k++) {
			if(k&mp[i]||(k<<1)&k||(k>>1)&k) 
				continue;
			a[i][++a[i][0]]=k;
		}
	}
	for(i=1;i<=a[1][0];i++) 
		f[1][i]=1;
	return;
}
int main()
{
//	freopen("1.in","r",stdin);
	Init();
	int i,j,k,u,v;
	int x,y,z;
	for(i=2;i<=n;i++) {
		for(j=1;j<=a[i][0];j++) {
			u=a[i][j];
			for(k=1;k<=a[i-1][0];k++) {
				v=a[i-1][k];
				if(u&v) continue;
				f[i][j]=(f[i][j]+f[i-1][k])%MOD;
			}
		}
	}
	LL ans=0;
	for(i=1;i<=a[n][0];i++) 
		ans=(ans+f[n][i])%MOD;
	cout<<ans%MOD<<endl;
	return 0;
}

ybt 1592 国王
[题目描述]
在 n×n 国际象棋的棋盘上放 k 个国王，国王可攻击相邻的 8 个格子，求使它们无法互相攻击的方案总数。
【输入】
只有一行，包含两个整数 n 和 k。
【输出】
每组数据一行为方案总数，若不能够放置则输出 。
【输入样例】

3 2

【输出样例】

16

思路
与牧场类似，我们按行放国王，本行放置国王的方案可以从子问题（上一行放置国王的状态）得出。

Code

#include
#include
#define LL long long
using namespace std;
const int N=10+2;
const int M=N*N;
const int S=(1<<N)+1;
const int Max_cnt=144+256+256;
LL a[Max_cnt];
LL p[Max_cnt];
LL f[N][M][Max_cnt];
int n,m;
int cnt;
#define lowbit(x) (x&(-x))
LL count(int x)
{
	LL res=0;
	for(;x>0;x-=lowbit(x)) 	
		res++;
	return res;
}
void deal_first()
{
	int i,j;
	cnt=0;
	for(i=0;i<=(1<<n)-1;i++) {
		if((i<<1)&i||(i>>1)&i) 
			continue;
		a[++cnt]=i;
		p[cnt]=count(i);
	}
	for(i=1;i<=cnt;i++) 
		f[1][p[i]][i]++;
	return;
}
LL ans=0;
int main()
{
	
	scanf("%d%d",&n,&m);
	deal_first();
	int i,j,k,u,v,e,o;
	for(i=2;i<=n;i++) { //枚举行 
		for(k=1;k<=cnt;k++) { //现在这一层方案 
			for(j=p[k];j<=m;j++) { //枚举国王数量 
				for(v=1;v<=cnt;v++) { //上一层方案 
					if((a[k]&a[v])||((a[k]<<1)&a[v])||((a[k]>>1)&a[v])) 
						continue;
					f[i][j][k]=f[i][j][k]+f[i-1][j-p[k]][v];
				}
			} 
		}
	}
	ans=0;
	for(i=1;i<=cnt;i++) 
		ans=ans+f[n][m][i];
	printf("%lld",ans);
	return 0;
}

洛谷P2704 炮兵阵地
描述
司令部的将军们打算在NM的网格地图上部署他们的炮兵部队。
一个NM的地图由N行M列组成，地图的每一格可能是山地（用”H” 表示），也可能是平原（用”P”表示），如下图。在每一格平原地形上最多可以布置一支炮兵部队（山地上不能够部署炮兵部队）；
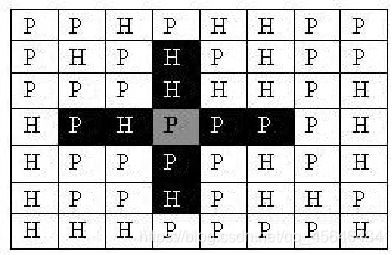
一支炮兵部队在地图上的攻击范围如图中黑色区域所示：
如果在地图中的灰色所标识的平原上部署一支炮兵部队，则图中的黑色的网格表示它能够攻击到的区域：沿横向左右各两格，沿纵向上下各两格。图上其它白色网格均攻击不到。
从图上可见炮兵的攻击范围不受地形的影响。 现在，将军们规划如何部署炮兵部队，在防止误伤的前提下（保证任何两支炮兵部队之间不能互相攻击，即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内），在整个地图区域内最多能够摆放多少我军的炮兵部队。

输入
第一行包含两个由空格分割开的正整数，分别表示N和M；
接下来的N行，每一行含有连续的M个字符(‘P’或者’H’)，中间没有空格。按顺序表示地图中每一行的数据。
输出
输出仅一行，包含一个整数K，表示最多能摆放的炮兵部队的数量。
样例输入

5 4
PHPP
PPHH
PPPP
PHPP
PHHP

样例输出

6

数据范围

0<=N <= 100；0<=M <= 10。

一行的状态由前两行得出，所以$f$数组除了要开行的一维外，还要再开两维，分别存储这一行的摆法和上一行的摆法。
同样要使用预处理。（预处理可以筛掉大量的无用状态）；
Code：

#include
#include
#define LL long long
using namespace std;
const int N=100+5;
const int M=10+1;
const int S=(1<<M)+5;
int n,m;
int f[N][S][S];
int p[N];
int a[S];
struct state
{
	int st[100];
	int c[100];
	int num;
};
state s[N];
#define lowbit(x) ((x)&(-(x)))
int count(int x)
{
	int res=0;
	while(x) {
		x-=lowbit(x);
		res++;
	}
	return res;
}
void Init(int h)
{
	s[h].num=0;
	for(int i=0;i<=(1<<m)-1;i++) {
		if((i&p[h])||((i>>1)&i)||((i<<1)&i)||((i>>2)&i)||((i<<2)&i))
			continue;
		s[h].st[++s[h].num]=i;
		s[h].c[s[h].num]=count(i);
	}
	return;
}
int main()
{
	//freopen("1.in","r",stdin);
	scanf("%d%d",&n,&m);
	int i,j,k,e,u,v;
	int x,y,z;
	char c;
	for(i=1;i<=n;i++) {
		for(j=1;j<=m;j++) {
			cin>>c;
			if(c=='P') p[i]=(p[i]<<1);
			else p[i]=(p[i]<<1)|1;
		}
		Init(i);
	}
	for(i=1;i<=s[1].num;i++) {
		f[1][i][1]=s[1].c[i];
	}
	s[0].num=1;
	s[0].st[1]=0;
	int ans=-1;
	for(i=2;i<=n;i++) {
		for(j=1;j<=s[i].num;j++) {
			u=s[i].st[j];
			for(k=1;k<=s[i-1].num;k++) {
				v=s[i-1].st[k];
				if(u&v) continue;
				for(e=1;e<=s[i-2].num;e++) {
					z=s[i-2].st[e];
					if(u&z||v&z) continue;
					f[i][j][k]=max(f[i][j][k],f[i-1][k][e]+s[i].c[j]);
				}
				ans=max(ans,f[i][j][k]);
			}
		}	
	}
	for(i=1;i<=s[n].num;i++) 
		for(j=1;j<=s[i-1].num;j++)
			ans=max(ans,f[n][i][j]);
	cout<<ans;
	return 0;
}

-------------------我是分割线------------------------------------------------------3.11
划重点*
棋盘
题目描述
求N行M列的图形分割成12的图形，有几种种方案。
例如23图形，共有3种方案。

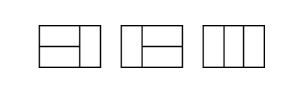
2*4图形，共有5种方案。如下图：

数据范围
1≤N,M≤11

输入格式
包含两个整数N和M。
输出格式
输出一个结果，表示方案数。

输入样例1：

2 4

输出样例2：

5

输入样例2：

4 11

输出样例2：

51205

思路
对于一个格子，在处理过程中可能有三种状态
所以，三进制状压？？
完全不用
因为最后格子是全部放满的，所以用1表示竖的格子的上面一位

先放满竖的格子，再放横的格子时有且只有一种方案；（那么我们用二进制就可以枚举出所有方案）
比如这种方案

二进制表示为

0011
0000

显然竖的格子要保证是合法的；
那怎么保证竖的格子是合法的呢？
可以这样考虑
任意相邻的两行01串结合只有4种情况，即：

1 0 1 0
0 1 1 0

第一种和第二种情况 肯定可以
第三种情况不行（格子重复了）
(U&V)!=1
第四种情况两行都没填竖的格子
所以要考虑放横的格子是否合法

显然只有连续的0为偶数个时才合法
Code：

#include
#include
#define LL long long
using namespace std;
const int N=11+1;
const int S=(1<<N)+5;
unsigned long long f[N][S];
bool law[S];
int n,m;
void Init() //预处理出所有0为偶数的状态，判断u|v即可
{
	int i,j,k,u;
	int cnt;
	const int s=(1<<m)-1;
	for(i=0;i<=s;i++) {
		cnt=0;  //计数器
		u=i;
		for(j=1;j<=m;j++) {
			if(u&1) {
				if(cnt&1) {
					law[i]=true; //fault 
					break;
				}
				cnt=0;
			} 
			else cnt++;
			u>>=1;
		}
		if(cnt&1) law[i]=true;
	}
	return;
}
void dp()
{
	int i,j,k;
	const int s=(1<<m)-1;
	f[0][0]=1;
	for(i=1;i<=n;i++) {
		for(j=0;j<=s;j++) {
			for(k=0;k<=s;k++) {
				if(j&k||law[j|k]) continue;
				f[i][j]+=f[i-1][k];
			}
		}
	}
}
int main()
{
	freopen("chess.in","r",stdin);
	freopen("chess.out","w",stdout);
	scanf("%d%d",&n,&m);
	Init();
	dp();
	cout<<f[n][0];
	return 0;
}

Code（2）：
更全面的预处理
先预处理出所有两两相邻合法的状态，再进行DP

#include
#include
#include
#include
#define LL long long
using namespace std;
const int N=11+1;
const int S=(1<<N)+5;
unsigned LL f[N][S];
int n,m;
vector<int> v[S]; //用vector存可相邻的状态，类似邻接表
bool law[S];
void Init()
{
	int i,j,u;
	int cnt;
	const int s=(1<<m)-1;
	for(i=0;i<=s;i++) {
		cnt=0;
		u=i;
		for(j=1;j<=m;j++) {
			if(u&1) {
				if(cnt&1) {
					law[i]=true; //fault 
					break;
				}
				cnt=0;
			} 
			else cnt++;
			u>>=1;
		}
		if(cnt&1) law[i]=true;
	}
	for(i=0;i<=s;i++) {
		for(j=0;j<=s;j++) {
			if(i&j||law[i|j]) 
				continue;
			v[i].push_back(j);
		}
	}
	return;
}
void dp()
{
	int i,j,k;
	f[0][0]=1;
	const int s=(1<<m)-1;
	for(i=1;i<=n;i++) {
		for(j=0;j<=s;j++) {
			for(k=0;k<v[j].size();k++) {
				f[i][j]+=f[i-1][v[j][k]];
			}
		}
	}
}
int main()
{
	freopen("chess.in","r",stdin);
	freopen("chess.out","w",stdout);
	scanf("%d%d",&n,&m);
	Init();
	dp();
	printf("%llu",f[n][0]);
	return 0;
}

然而提交时只需要一张表 w(ﾟДﾟ)w

#include
#include
#include
#define LL long long
using namespace std;
const int N=11+25;
int n,m;
unsigned long long f[N][N]=
{
{0,},
{0,0,1,0,1,0,1,0,1,0,1,0,},
{0,1,2,3,5,8,13,21,34,55,89,144,},
{0,0,3,0,11,0,41,0,153,0,571,0,},
{0,1,5,11,36,95,281,781,2245,6336,18061,51205,},
{0,0,8,0,95,0,1183,0,14824,0,185921,0,},
{0,1,13,41,281,1183,6728,31529,167089,817991,4213133,21001799,},
{0,0,21,0,781,0,31529,0,1292697,0,53175517,0,},
{0,1,34,153,2245,14824,167089,1292697,12988816,108435745,1031151241,8940739824,},
{0,0,55,0,6336,0,817991,0,108435745,0,14479521761,0,},
{0,1,89,571,18061,185921,4213133,53175517,1031151241,14479521761,258584046368,3852472573499,},
{0,0,144,0,51205,0,21001799,0,8940739824,0,3852472573499,0,},
};
int main()
{
	freopen("chess.in","r",stdin);
	freopen("chess.out","w",stdout);
	cin>>n>>m;
	cout<<f[n][m];
	return 0;
}

φ(≧ω≦)♪

小结：可以看出这一类问题都是先预处理出每一行的状态 再自上而下，逐层求解；

另一类问题

类似于哈密顿回路的问题
Hamilton路径
给定一张 n 个点的带权无向图，点从 0~n-1 标号，求起点 0 到终点 n-1 的最短Hamilton路径。 Hamilton路径的定义是从 0 到 n-1 不重不漏地经过每个点恰好一次。
输入格式
第一行输入整数n。接下来n行每行n个整数，其中第i行第j个整数表示点i到j的距离（记为a[i,j]）。
对于任意的x,y,z，数据保证 a[x,x]=0，a[x,y]=a[y,x] 并且 a[x,y]+a[y,z]>=a[x,z]。
输出格式
输出一个整数，表示最短Hamilton路径的长度。
数据范围1≤n≤20 , 0≤a[i,j]≤10^7
输入样例：

5
0 2 4 5 1
2 0 6 5 3
4 6 0 8 3
5 5 8 0 5
1 3 3 5 0

输出样例：

18

如何描述状态？
dp[i][j]表示当前已经走过点的集合为i，移动到j。
已经走过点的集合i，如何描述？
状压：
假如走过0,1,4这三个点，我们用二进制10011就可以表示，2,3没走过所以是0
那么走过点的集合i中去除掉点j也很容易表示i - (1 << j)，比方说i是{0,1,4}，j是1，那么i = 10011，(1 << j) = 000010，i - (1 << j) = 10001
状态转移方程如何设置？
就是找一个中间点k，将已经走过点的集合i中去除掉j（表示j不在经过的点的集合中），然后再加上从k到j的权值
dp代码

for (int i = 0; i < (1 << n); i++) // i代表走过的点的集合
   for(int j = 0; j < n; j++)//枚举当前到了哪一个点
     if ((i >> j & 1) == 1) //如果i集合中第j位是1，也就是到达过j这点
       for (int k = 0; k < n; k++) //枚举k，通过k中转到j
         if ((i-(1<< j)>>k&1)==1)//i中去除掉点j后包含k点
            dp[i][j] = min(f[i][j],f[i^(1<<j)][k]+map[k][j]);

   f[1][0]=0;
   //第一个点是不需要任何费用的

 cout<<f[(1<<n)-1][n-1];//输出最后的最优值

时间复杂度： n为20的时候，外层循环(1<<20)，内层循环20，所以整体时间复杂度O(2020220)，这比O(n!)快多了

洛谷 P1433 吃奶酪
题目描述
房间里放着 n 块奶酪。一只小老鼠要把它们都吃掉，问至少要跑多少距离？老鼠一开始在 (0,0) 点处。
输入格式
第一行一个正整数 n。
接下来每行 2 个实数，表示第i块奶酪的坐标。
两点之间的距离公式为 $\sqrt{(x1-x2{)}^2+(y1-y2{)}^2}$
输出格式
一个数，表示要跑的最少距离，保留 22 位小数。
输入输出样例
输入 #1

4
1 1
1 -1
-1 1
-1 -1

输出 #1

7.41

说明/提示
$1\le n\le 15$
Code：

#include
#include
#include
#include
#define LL long long
using namespace std;
const int N=15+2;
const int S=(1<<N)+5;
const double INF=100000000.00;
int n;
struct node
{
	double x,y;
}a[N];
double w[N][N];
double dis(int x,int y)
{
	return sqrt((a[x].x-a[y].x)*(a[x].x-a[y].x)+(a[x].y-a[y].y)*(a[x].y-a[y].y));
}
double f[N][S]; //now -> N ; have S down
int main()
{
	scanf("%d",&n);
	int i,j,k,e,u,v,r;
	for(i=1;i<=n;i++) 
		scanf("%lf%lf",&a[i].x,&a[i].y);
	for(i=1;i<=n;i++) {
		w[i][i]=0.0;
		for(j=i+1;j<=n;j++) {
			w[j][i]=w[i][j]=dis(i,j);
		}
	}
	memset(f,127,sizeof f);
	for(i=1;i<=(1<<n)-1;i++) { // all S
		for(j=1;j<=n;j++) {
			if(!(i>>(j-1)&1)) continue;
			v=i^(1<<(j-1));
			for(k=1;k<=n;k++) {
				if(!(v>>(k-1)&1)) continue;
				f[j][i]=min(f[j][i],f[k][v]+w[k][j]);
			}
			if(v==0) 
				f[j][i]=min(f[j][i],dis(j,16));
		}
	}
	const int s=(1<<n)-1;
	double ans=f[0][0]+1.1;
	for(i=1;i<=n;i++) {
		ans=min(ans,f[i][s]);
	}
	printf("%.2f\n",ans);
	return 0;
}