LeetCode|动态规划|1035. 不相交的线 、53. 最大子数组和
目录
一、1035. 不相交的线
1.题目描述
2.解题思路
3.代码实现
二、53. 最大子数组和
1.题目描述
2.解题思路
3.代码实现(动态规划解法)
一、1035. 不相交的线
1.题目描述
在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。
现在,可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线,这些直线需要同时满足满足:
-
nums1[i] == nums2[j] - 且绘制的直线不与任何其他连线(非水平线)相交。
请注意,连线即使在端点也不能相交:每个数字只能属于一条连线。
以这种方法绘制线条,并返回可以绘制的最大连线数。
示例 1:
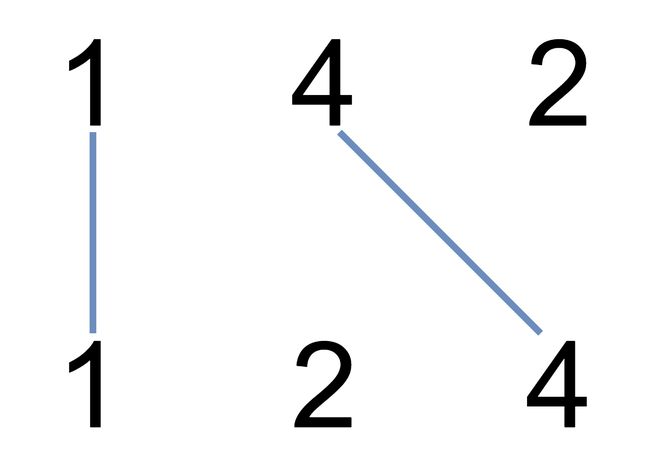
输入:nums1 = [1,4,2], nums2 = [1,2,4] 输出:2 解释:可以画出两条不交叉的线,如上图所示。 但无法画出第三条不相交的直线,因为从 nums1[1]=4 到 nums2[2]=4 的直线将与从 nums1[2]=2 到 nums2[1]=2 的直线相交。
示例 2:
输入:nums1 = [2,5,1,2,5], nums2 = [10,5,2,1,5,2] 输出:3
示例 3:
输入:nums1 = [1,3,7,1,7,5], nums2 = [1,9,2,5,1] 输出:2
2.解题思路
- 发现这道题目的本质就不难:两两相等能连线,并且线不能相交。其实就是求最长公共子序列
3.代码实现
class Solution {
public:
int maxUncrossedLines(vector& nums1, vector& nums2) {
//这道题的本质就是求最长公共子序列---这里的子序列是不改变数组中的原来相对顺序,并不一定要连续的
vector> dp(nums1.size()+1,vector(nums2.size()+1,0));
for(int i = 1;i <= nums1.size();i++){
for(int j = 1; j <= nums2.size();j++){
if(nums1[i-1]== nums2[j-1]){
dp[i][j] = dp[i-1][j-1] + 1;
}
else{
dp[i][j] = max(dp[i-1][j],dp[i][j-1]);
}
}
}
return dp[nums1.size()][nums2.size()];
}
}; 二、53. 最大子数组和
1.题目描述
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组 是数组中的一个连续部分。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4] 输出:6 解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
示例 2:
输入:nums = [1] 输出:1
示例 3:
输入:nums = [5,4,-1,7,8] 输出:23
2.解题思路
- 本题前面发过贪心的解法,现在用动态规划解题
- 详情看代码注释
3.代码实现(动态规划解法)
class Solution {
public:
int maxSubArray(vector& nums) {
//明确dp数组含义:下标到i为止的,最大和为dp[i]
vector dp(nums.size(),0);
if(nums.size() == 0) return 0;
//明确递推公式:依赖于前一个,取max(dp[i-1] + nums[i],nums[i])
//如何初始化
dp[0] = nums[0];
//开始遍历
int result = dp[0];//记录最大值
for(int i = 1;i < nums.size();i++){
dp[i] = max(dp[i-1]+ nums[i],nums[i]);
result = max(result,dp[i]);
}
return result;
}
};