Leetcode#53 Maximum Subarray

原题地址

 

方法I：动态规划

另sum[i]表示从i开始的最大子串和，则有递推公式：sum[i] = max{A[i], A[i] + sum[i+1]}

因为递推式只用到了后一项，所以在编码实现的时候可以进行状态压缩，用一个变量即可

代码：

 1 int maxSubArray(int A[], int n) {
 2   int sum = A[n - 1];
 3   int maxSum = sum;
 4 
 5   for (int i = n - 2; i >= 0; i--) {
 6     sum = max(A[i], sum + A[i]);
 7     maxSum = max(maxSum, sum);
 8   }
 9 
10   return maxSum;
11 }

时间复杂度O(n)，空间复杂度O(1)

 

方法II：扫描法（姑且这么称呼吧）

这是网上比较流行的一种做法，本质上还是动态规划+状态压缩。参考这篇博文

代码：

 1 int maxSubArray(int A[], int n) {
 2   if (n == 0)
 3     return 0;
 4 
 5   int max_ending_here = A[0];
 6   int max_so_far = A[0];
 7   for(int i = 1; i < n; ++i)
 8     {
 9       if (max_ending_here < 0)
10         // So far we get negative values, this part has to be dropped
11         max_ending_here = A[i];
12       else
13         // we can accept it, it could grow later
14         max_ending_here += A[i];
15 
16       max_so_far = max(max_so_far, max_ending_here);
17     }
18   return max_so_far;
19 }

时间复杂度O(n)，空间复杂度O(1)

 

方法III：分治法

假设求A[l..r]的最大子串和

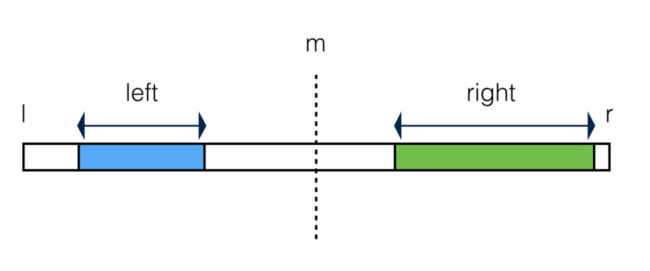
首先将其分成两半A[l..m]和A[m+1..r]，其中m=(l+r)/2，并分别求递归求出这两半的最大子串和，不妨称为left，right。如下图所示：

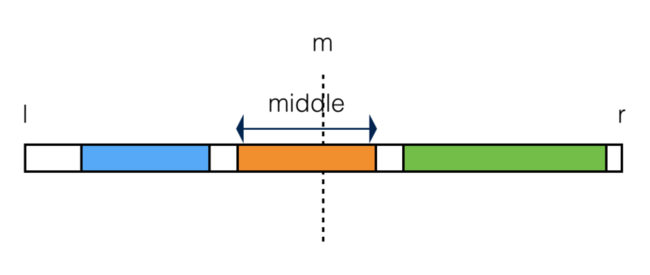
A[l..r]的连续子串和可能出现在左半边（即left），或者可能出现在右半边（即right），还可能出现在横跨左右两半的地方（即middle），如下图橙色部分所示：

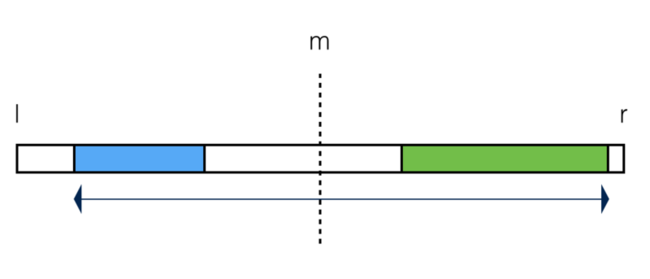
当然，middle完全有可能覆盖left或right，它可能的范围入下图所示：

那么，如何求middle？貌似没有什么简单的方法，只能从中间向两遍扫，也就是把上图种的范围扫一遍。具体怎么扫呢？见方法I和方法II

是不是突然觉得很坑爹？既然知道最后求middle要扫一遍，还不如一开始就从l到r扫一遍求max得了，还费什么劲儿求left和right呢？求left和right的作用仅限于缩小扫描的范围。

代码：

 1 int diveNConquer(int A[], int l, int r) {
 2   if (l == r)
 3     return A[l];
 4 
 5   int m = (l + r) / 2;
 6   int left = diveNConquer(A, l, m);
 7   int right = diveNConquer(A, m + 1, r);
 8   int middle = A[m];
 9   for (int i = m - 1, tmp = middle; i >= l; i--) {
10     tmp += A[i];
11     middle = max(middle, tmp);
12   }
13   for (int i = m + 1, tmp = middle; i <= r; i++) {
14     tmp += A[i];
15     middle = max(middle, tmp);
16   }
17 
18   return max(middle, max(left, right));
19 }
20 
21 int maxSubArray(int A[], int n) {
22   return diveNConquer(A, 0, n - 1);
23 }

分析一下时间复杂度，设问题的工作量是T(n)，则有T(n) = 2T(n/2) + O(n)，解得T(n) = O(nlogn)。看看，效率反而低了不少。