算法面试与实战-02排序算法- 时间复杂度为O(nlogn)的排序算法（快速排序）

hi~各位新年已过，中间苗某小小的休息了一下，其实在家好无聊，不想动~但是学习还是不能断，武汉加油，中国加油。

好了我们继续学习排序算法。

上期我们说了时间复杂度为O(n2)的排序算法-以冒泡排序为例。

本期我们学习时间复杂度为O(nlogn)的排序算法：

• 快速排序
• 归并排序
• 堆排序

本篇介绍快速排序的原理。

1、概念

为啥快速排序比冒泡排序快呢，因为快速排序用了分治法的思想。同冒泡排序一样，快速排序也属于交换排序，通过元素之间的比较和交换位置来达到排序的目的。

不同的是，冒泡排序在每一轮只把一个元素冒泡到数列的一端，而快速排序在每一轮挑选一个基准元素，并让其他比它大的元素移动到数列一边，比它小的元素移动到数列的另一边，从而把数列拆解成了两个部分。如下图：

其实就是以某一个元素为界，对于左边的任意元素都小于右边任一元素。而这种思想就叫做分治法，分而治之。每次把数列分成两部分，究竟有什么好处呢？我们举例说明：

假如给定8个元素的数列，一般情况下冒泡排序需要比较8轮，每轮把一个元素移动到数列一端，时间复杂度是O（n^2）。但是如果使用分治法的话就是这样。

如图所示，在分治法的思想下，原数列在每一轮都被拆分成两部分，每一部分在下一轮又分别被拆分成两部分，直到不可再分为止。每一轮的比较和交换，需要把数组全部元素都遍历一遍，时间复杂度是O(n)。这样的遍历一共需要多少轮呢？假如元素个数是n，那么平均情况下需要logn轮，因此快速排序算法总体的平均时间复杂度是O(nlogn)。

基准元素的选择， 以及元素的交换， 都是快速排序的核心问题。 让我们先来看看如何选择基准元素。

2、基准元素的选择

基准元素，英文是pivot，在分治过程中，以基准元素为中心，把其他元素移动到它的左右两边。那么如何获取这个基准元素的呢？最简单的方式是选择数列的第1个元素。

这种选择在绝大多数情况下是没有问题的。 但是，假如有一个原本逆序的数列，期望排序成顺序数列，那么会出现什么情况呢？
 

发现数列并没有分成两半，每一次轮询只是确定基准元素的位置。在这种情况下， 数列的第1个元素要么是最小值，要么是最大值， 根本无法发挥分治法的优势。在这种极端情况下， 快速排序需要进行n轮， 时间复杂度退化成了O(n^2)。那么，该怎么避免这种情况发生呢？我们可以随机选择一个元素作为基准元素，并且让基准元素和数列首元素交换位置。

这样一来，即使在数列完全逆序的情况下，也可以有效地将数列分成两部分。当然，即使是随机选择基准元素，也会有极小的几率选到数列的最大值或最小值，同样会影响分治的效果。所以，虽然快速排序的平均时间复杂度是O(nlogn)，但最坏情况下的时间复杂度是O(n^2)。

在后文中，为了简化步骤，省去了随机选择基准元素的过程，直接把首元素作为基准元素。

3、元素的交换

选定了基准元素以后，我们要做的就是把其他元素中小于基准元素的都交换到基准元素一边，大于基准元素的都交换到基准元素另一边。

具体如何实现呢？有两种方法。

1. 挖坑法
2. 单边循环法

何谓挖坑法？我们来看一看详细过程。给定原始数列如下，要求从小到大排序：

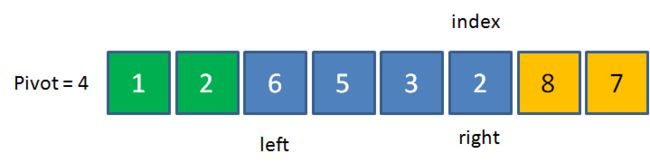
首先，我们选定基准元素Pivot，并记住这个位置index，这个位置相当于一个“坑”。并且设置两个指针left和right，指向数列的最左和最右两个元素：

接下来，从right指针开始，把指针所指向的元素和基准元素做比较。如果比pivot大，则right指针向左移动；如果比pivot小，则把right所指向的元素填入坑中。在当前数列中，1<4，所以把1填入基准元素所在位置，也就是坑的位置。这时候，元素1本来所在的位置成为了新的坑。同时，left向右移动一位。

此时，left左边绿色的区域代表着小于基准元素的区域。

接下来，我们切换到left指针进行比较。如果left指向的元素小于pivot，则left指针向右移动；如果元素大于pivot，则把left指向的元素填入坑中。在当前数列中，7>4，所以把7填入index的位置。这时候元素7本来的位置成为了新的坑。同时，right向左移动一位。

此时，right右边橙色的区域代表着大于基准元素的区域。

下面按照刚才的思路继续排序：8>4，元素位置不变，right左移

2<4，用2来填坑，left右移，切换到left。

6>4，用6来填坑，right左移，切换到right。

3<4，用3来填坑，left右移，切换到left。

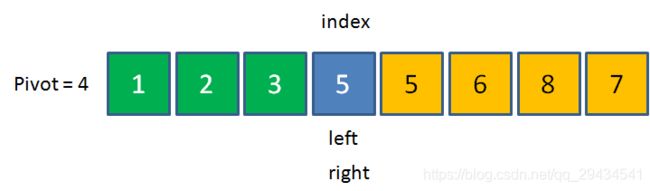
5>4，用5来填坑，right右移。这时候left和right重合在了同一位置。

这时候，把之前的pivot元素，也就是4放到index的位置。此时数列左边的元素都小于4，数列右边的元素都大于4，这一轮交换终告结束。

填坑法大致思想就是这样，那么他的代码是如何实现呢？如下：

public class QuickSort {
    public static void quickSort(int[] arr,int startIndex,int endIndex){
        //递归结束条件：startIndex大于等于endIndex的时候
        if (startIndex>=endIndex){
            return;
        }
        //得到基准元素位置
        int prvoIndex =partition(arr,startIndex,endIndex);
        //用分治法递归数列的两部分
        quickSort(arr,startIndex,prvoIndex-1);
        quickSort(arr,prvoIndex+1,endIndex);
    }
    private static int partition(int[] arr,int startIndex,int endIndex){
        //取第一个位置的元素作为基准元素
        int pivot=arr[startIndex];
        int left=startIndex;
        int right=endIndex;
        //坑的位置，初始等于pivot的位置
        int index=startIndex;
        //大循环在左右指针重合或者交错时结束
        while (right>=left){
            //right指针从左向右进行比较
            while (right>=left){
                if (arr[right]=left){
                if (arr[left]>pivot){
                    arr[right]=arr[left];
                    index=left;
                    right--;
                    break;
                }
                left++;
            }
        }
        arr[index]=pivot;
        return index;
    }

    public static void main(String[] args) {
        int[] arr = {4, 7, 6, 3, 2, 8, 1};
        quickSort(arr,0,arr.length-1);
        for (int a:arr) {
            System.out.print(a+" ");
        }
    }
}

代码中，quickSort方法通过递归的方式，实现了分而治之的思想。partition方法则实现元素的移动，让数列中的元素依据自身大小，分别移动到基准元素的左右两边。在这里，我们使用移动方式是挖坑法。此外还有实现元素的交换可以使用指针交换的方法。

指针交换法：

何谓指针交换法？我们来看一看详细过程。

给定原始数列如下，要求从小到大排序：

 

开局和挖坑法相似，我们首先选定基准元素Pivot，并且设置两个指针left和right，指向数列的最左和最右两个元素：

接下来是第一次循环，从right指针开始，把指针所指向的元素和基准元素做比较。如果大于等于pivot，则指针向左移动；如果小于pivot，则right指针停止移动，切换到left指针。

在当前数列中，1<4，所以right直接停止移动，换到left指针，进行下一步行动。轮到left指针行动，把指针所指向的元素和基准元素做比较。如果小于等于pivot，则指针向右移动；如果大于pivot，则left指针停止移动。由于left一开始指向的是基准元素，判断肯定相等，所以left右移一位。

由于7 > 4，left指针在元素7的位置停下。这时候，我们让left和right指向的元素进行交换。

 

接下来，我们进入第二次循环，重新切换到right向左移动。right先移动到8，8>4，继续左移。由于2<4，停止在2的位置。

切换到left，6>4，停止在6的位置。

元素6和2交换。

进入第三次循环，right移动到元素3停止，left移动到元素5停止。

元素5和3交换。

进入第四次循环，right移动到元素3停止，这时候请注意，left和right指针已经重合在了一起。

当left和right指针重合之时，我们让pivot元素和left与right重合点的元素进行交换。此时数列左边的元素都小于4，数列右边的元素都大于4，这一轮交换终告结束。

下面我们来看看代码是如何实现的？

public class QuickSort {
    public static void quickSort(int[] arr,int startIndex,int endIndex){
        //递归结束天界：startIndex大等于endIndex的时候
        if (startIndex>=endIndex){
            return;
        }
        //得到基准元素位置
        int pivoIndex=partition(arr,startIndex,endIndex);
        quickSort(arr,startIndex,pivoIndex-1);
        quickSort(arr,pivoIndex+1,endIndex);
    }
    private static int partition(int[] arr,int startIndex,int endIndex){
        //取第一个位置的元素作为基准元素
        int pviot=arr[startIndex];
        int left=startIndex;
        int right=endIndex;
        while (left!=right){
            //控制right指针比较并左移
            while (leftpviot){
                right--;
            }
            //控制right指针比较并右移
            while (left

快速排序的就介绍到这里啦，下期我们继续~