机器学习之PyTorch和Scikit-Learn第3章 使用Scikit-Learn的机器学习分类器之旅Part 1

其它章节内容请见机器学习之PyTorch和Scikit-Learn

本章中，我们会学习一些学术界和工业界常用的知名强大机器学习算法。在学习各种用于分类的监督学习算法的不同时，我们还会欣赏到它们各自的优势和劣势。另外，我们会开始使用scikit-learn库，它为高效、有生产力地使用这些算法提供了用户友好且一致的接口。

本章讲解的主要内容有：

• 介绍用于分类的健壮知名算法，如逻辑回归、支持向量机、决策树和K-近邻算法
• 使用scikit-learn机器学习库的示例和讲解，它通过用户友好的Python API提供了大量的机器学习算法
• 讨论线性和非线性决策边界分类器的优势和不足

选择分类算法

为具体的问题任务选择合适的分类算法需要实践和经验加持，每种算法都有自己的局限，是基于一些假设前提的。套用David H. Wolpert所提的没有免费午餐定理，没有哪个分类器对所有场景都表现最佳（《学习算法间缺少先验差别》，D.H. Wolpert, 1996: 1341-1390）。在实践中，推荐至少对比一部分线性算法的表现来选择具体问题的最佳模型，可能随特征或样本的不同、数据集中噪声的数量以及类是否线性可分割而不同。

最终分类器的表现-计算性能以及预测能力-极度依赖于底层供学习的数据。我们训练机器学习算法可概括为如下5个步骤：

1. 选择特征及收集打标签的训练样本
2. 选择性能指标
3. 选择学习算法及训练模型
4. 评估模型的表现
5. 修改算法的配置并对模型调优

因本书采取逐步构建机器学习知识库的方式，我们会在本章集中讲解不同算法的核心概念，后续再详细讨论特征选取和预处理、性能指标及超参数调优。

学习scikit-learn的第一步-训练感知机

在第2章 为分类训练简单机器学习算法中，我们学习了用于分类的两种相关联算法，感知机学习规则和自适应线性神经网络，也通过Python和NumPy进行了实现。下面我们要学习scikit-learn API，它将用户友好度与一致性接口和调度优化的多种分类算法实现相结合。scikit-learn库不止提供了大量的学习算法，还有很多的方便的函数进行数据预处理、调优及评估模型。我们会在第4章 构建优秀训练数据集 - 数据预处理和第5章 通过降维压缩数据 中详细讨论其底层概念。

开启对scikit-learn库的学习，我们会先训练一个类似第2章 为分类训练简单机器学习算法中的感知机模型，在以下各小节中使用到的是已经很熟悉的鸢尾花数据集。为使用方便，scikit-learn中已经内置了鸢尾花数据集，因为它是测试和试验算法时常用的简单、知名数据集。和上一章一样，为方便可视化我们只使用鸢尾花数据集中的两个特征。

我们将150个花样本的花萼长度和花瓣长度赋值给特征矩阵X，花品种的类标签则赋值给向量数组y：

>>> from sklearn import datasets
>>> import numpy as np
>>> iris = datasets.load_iris()
>>> X = iris.data[:, [2, 3]]
>>> y = iris.target
>>> print('Class labels:', np.unique(y))
Class labels: [0 1 2]

np.unique(y)函数返回iris.target中存储的三个唯一类标签，可以看到鸢尾花的类名Iris-setosa、Iris-versicolor和Iris-virginica，已经存储为了整数（此外为: 0, 1, 2）。虽然很多scikit-learn函数和类方法也能处理字符串格式的类标签，但更推荐使用整型标签，这样可以避免技术问题并因占用内存较小而提升计算性能，此外，将类标签编码为整型是机器学习库中常见的一种约定。

为评估训练对未知数据的表现如何，我们会进一步将数据集分为训练数据集和测试数据集。在第6章 学习模型评估和超参数调优的最佳实践中，我们会详细讨论模型评估相关的最佳实践。使用scikit-learn中model_selection模块的train_test_split函数，我们随机地将数组X和y分割成30%的测试数据（45个样本）和70%的训练数据（105个样本）：

>>> from sklearn.model_selection import train_test_split
>>> X_train, X_test, y_train, y_test = train_test_split(
...     X, y, test_size=0.3, random_state=1, stratify=y
... )

注意train_test_split函数已经在分割前对训练数据集进行了内部打散，否则，训练集中的所有样本都是类0和类1，而测试集会包含45个来自类2的样本。通过random_state参数，我们为用于在分割前打散数据集的伪随机数生成器提供了固定的随机种子(random_state=1) 。使用固定的random_state可保证我们的结果可重现。

最后，我们通过stratify=y使用了对分层的内置支持。在这里，分层表示train_test_split方法返回具有相同比例的类标签训练集和测试集作为输入数据集。我们可以使用NumPy中用于统计数组中各个值出现次数的bincoun函数，来难是否真的如此：

>>> print('Labels counts in y:', np.bincount(y))
Labels counts in y: [50 50 50]
>>> print('Labels counts in y_train:', np.bincount(y_train))
Labels counts in y_train: [35 35 35]
>>> print('Labels counts in y_test:', np.bincount(y_test))
Labels counts in y_test: [15 15 15]

很多机器学习和优化算法还要求使用特征缩放来优化性能，我们在第2章中提到梯度下降就出现过。这里我们会使用scikit-learn中preprocessing模块的StandardScaler类来标准化特征：

>>> from sklearn.preprocessing import StandardScaler
>>> sc = StandardScaler()
>>> sc.fit(X_train)
>>> X_train_std = sc.transform(X_train)
>>> X_test_std = sc.transform(X_test)

使用上述的代码，我们从preprocessing模块加载了StandardScaler类并初始化了一个新的StandardScaler对象，赋值给sc变量。使用fit方法，StandardScaler为训练数据中的每个特征维度评估了参数（样本均值）和（标准差）。然后通过调用transform方法，我们使用这些评估出的参数和标准化了训练数据。注意我们使用了同样的缩放参数来标准化测试数据集，这样训练集和测试集中的值可进行比较。

标准化好了训练数据后，现在可以训练感知模型了。scikit-learn中的大部分算法默认已通过一对剩余(OvR)方法支持多类别分类，这一方法允许我们同时喂入三种花的类别。代码如下：

>>> from sklearn.linear_model import Perceptron
>>> ppn = Perceptron(eta0=0.1, random_state=1)
>>> ppn.fit(X_train_std, y_train)

scikit-learn中接口提醒着我们第2章中的感知机实现。在从linear_model模块加载了Perceptron类后，我们初始化了新的Perceptron对象并通过fit方法进行了训练。这里的模型参数eta0等价于我们自己实现感知机时使用的学习率eta。

读者一定还记得在第2章中，寻找合适的学习率需要进行一些试验。如果学习率过大，算法会超出全局损失最小值。如果学习率过小，算法会需要更多次的迭代才能收敛，这会让学习变慢，尤其是对于大数据集。我们同样使用了random_state参数来保证每次迭代后训练集的初始打散可重现。

在scikit-learn中训练好模型后，我们可以使用predict方法来完成预测，这与第2章中我们实现的感知机相似。代码如下：

>>> y_pred = ppn.predict(X_test_std)
>>> print('Misclassified examples: %d' % (y_test != y_pred).sum())
Misclassified examples: 1

执行以上代码，我们会看到感知机对45个花样本的分类中有一个错误。因为，对测试集的分类误差率大约为0.022，或2.2%()。

分类误差与准确度

很多机器学习从业者不报告分类误差，而是报告模型的准确度，计算方法如下：

1–error = 0.978, 或97.8%

使用分类误差还是准确度取决于个人偏好。

scikit-learn模块还在metrics模块中实现了大量的性能指标。例如，我们可以这样计算感知机对测试集的分类准确度：

>>> from sklearn.metrics import accuracy_score
>>> print('Accuracy: %.3f' % accuracy_score(y_test, y_pred))
Accuracy: 0.978

这里，y_test是真实类标签，而y_pred是我们此前所预测的类标签。相对应的，scikit-learn中的每个分类器都有一个score方法，通过组合的predict调用和accuracy_score来计算预测准确度，如下所示：

>>> print('Accuracy: %.3f' % ppn.score(X_test_std, y_test))
Accuracy: 0.978

过拟合

注意我们是根据本章中的测试数据集来计算模型的表现。在第6章中，我们会学习到一些有用的技术，包括图形分析，比如学习曲线来检测和防止过拟合。本章稍后还会提到过拟合，它的意思是模型对训练数据所提取的模式很好，但对未知数据的表现不好。

最后，我们可以使用第2章中的plot_decision_regions函数来绘制新训练的感知机模型的决策区域，通过可视化的方式来看对花样本的分类表现如何。但我们来做一些小修改来通过小圆圈高亮显示测试集中的数据实例：

from matplotlib.colors import ListedColormap
import matplotlib.pyplot as plt
def plot_decision_regions(X, y, classifier, test_idx=None,
                          resolution=0.02):
    # setup marker generator and color map
    markers = ('o', 's', '^', 'v', '<')
    colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
    cmap = ListedColormap(colors[:len(np.unique(y))])
    # plot the decision surface
    x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),
                           np.arange(x2_min, x2_max, resolution))
    lab = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
    lab = lab.reshape(xx1.shape)
    plt.contourf(xx1, xx2, lab, alpha=0.3, cmap=cmap)
    plt.xlim(xx1.min(), xx1.max())
    plt.ylim(xx2.min(), xx2.max())
    # plot class examples
    for idx, cl in enumerate(np.unique(y)):
        plt.scatter(x=X[y == cl, 0],
                    y=X[y == cl, 1],
                    alpha=0.8,
                    c=colors[idx],
                    marker=markers[idx],
                    label=f'Class {cl}',
                    edgecolor='black')
    # highlight test examples
    if test_idx:
        # plot all examples
        X_test, y_test = X[test_idx, :], y[test_idx]
        
        plt.scatter(X_test[:, 0], X_test[:, 1],
                    c='none', edgecolor='black', alpha=1.0,
                    linewidth=1, marker='o',
                    s=100, label='Test set')

通过对plot_decision_regions函数所做的一点修改，我们指定了希望在结果图中标记的样本索引。代码如下：

>>> X_combined_std = np.vstack((X_train_std, X_test_std))
>>> y_combined = np.hstack((y_train, y_test))
>>> plot_decision_regions(X=X_combined_std,
...                       y=y_combined,
...                       classifier=ppn,
...                       test_idx=range(105, 150))
>>> plt.xlabel('Petal length [standardized]')
>>> plt.ylabel('Petal width [standardized]')
>>> plt.legend(loc='upper left')
>>> plt.tight_layout()
>>> plt.show()

在结果图中可以看出，线性决策边界并不能很好分出三种花：

图3.1 多类别感知机拟合鸢尾花数据集后的决策边界

但还记得在第2章中我们讨论过对无法完整线性分割的数据集感知机永远无法收敛，这也是为什么在实际应用中通常不推荐感知机算法。在下面的小节中，我们会学到更多强大的线性分类器，即使类无法完美地线性分割，也能收敛出损失最小值。

其它感知机配置

Perceptron，以及scikit-learn中的其它函数和类，通常一些为保持清晰而省略的参数。可以使用Python中的help函数来阅读更多这样的参数，也可以阅读scikit-learn优秀的在线文档http://scikit-learn.org/stable/。

通过逻辑回归建模分类概率

虽然感知机规则对机器学习分类算法是一个很好、很轻松的入门，但它有一个最大的缺陷是对非线性完美分割的类永远不会收敛。前一小节的分类任务就是这种场景的例子。这是由于每次迭代训练样本中都至少有一个分类错误导致权重一直在更新。当然我们可以修改学习率并增加迭代次数，但注意这一数据集的感知机永远不会收敛。

为节省我们的时间，接下来学习另一个简单但更强大的解决线性二元分类问题的算法：逻辑回归（logistic regression）。注意虽然名字里带回归，但这是一个分类模型，而不是回归模型。

逻辑回归和条件概率

逻辑回归是一个易于实现且对线性可分割模型类性能很好的分类模型。它是业界最常使用的分类算法之一。类似于感知机和自适应线性神经网络，本章中的逻辑回归模型也是一个用于二元分类的线性模型。

用于多类别的逻辑回归

线性逻辑回归可用于归纳多类场景，称为多类逻辑回归（multinomial logistic regression） ，或softmax回归。有关多类逻辑回归的详细讲解不在本书的范畴内，感兴趣的读者可以在作者的授课笔记中找到更多信息： https://sebastianraschka.com/pdf/lecture-notes/stat453ss21/L08_logistic__slides.pdf或https://www.youtube.com/watch?v=L0FU8NFpx4E。

另一种将逻辑回归用于多类场景的方式是通过OvR技术，这在前面已经讨论过。

为讲解逻辑回归作为二元分类概率模型背后的主要机制，我们先介绍几率（odds）：几率是指具体事件发生的比率。几率可写作$\frac{p}{(1-p)}$，其中p表示正事件（positive event）的概率。“正事件”不一定是好的，它指的是希望预测的事件，例如，有某种症状的病人患某一疾病的概念；可以把正事件想成是类标签y = 1，而症状是特征x。因此为保持简洁，可以将概率p定义为p := p(y = 1|x)，给定特征x时某一样本属于类1的条件概念。

然后我们可以进一步定义logit函数，它是对数发生比（log-odds）：

$$logit(p)=\log \frac{p}{(1-p)}$$

注意log指的是自然对数，这是计算机科学中常见的约定。logit函数接收0到1范围内的输入值，将它们转换为整个实数范围内的值。

在逻辑回归模型中，我们假设在加权输入（参见第2章中的净输入）和对数发生比之间存在线性关性：

$$logit(p)=w_1{x}_1+\cdots +w_m{x}_m+b=\sum _{x=j}{w}_j{x}_j+b=w^{T}x+b$$

虽然前面描述了对数发生比和净输入线性关联的假设，但我们实际感兴趣的是概率p，给定特性时样本的类成员概念。logit函数将概率与实际数字范围之间进行了映射，可以认为函数反过来就是实际数字范围对概率p的[0, 1]范围的映射。

这种logit的反向通常称为逻辑sigmoid函数，有时也因其典型的S形状简称为sigmoid函数：

$$\sigma (z)=\frac{1}{1+e^{-z}}$$

这里的z是净输入，权重和输入的线性组合（也即与训练样本相关联的特征）：

z = wTx + b

下面我们来简单绘制-7到7之间一些值的sigmoid函数来看下效果：

>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> def sigmoid(z):
...     return 1.0 / (1.0 + np.exp(-z))
>>> z = np.arange(-7, 7, 0.1)
>>> sigma_z = sigmoid(z)
>>> plt.plot(z, sigma_z)
>>> plt.axvline(0.0, color='k')
>>> plt.ylim(-0.1, 1.1)
>>> plt.xlabel('z')
>>> plt.ylabel('$\sigma (z)$')
>>> # y axis ticks and gridline
>>> plt.yticks([0.0, 0.5, 1.0])
>>> ax = plt.gca()
>>> ax.yaxis.grid(True)
>>> plt.tight_layout()
>>> plt.show()

执行以上示例代码后，我们会看到S形状的（sigmoidal）曲线：

图3.2：逻辑sigmoid函数的图形

可以看到在z趋向无穷大(z→∞) 时$\sigma (z)$趋向于1，因为在z很大时e–z会变得非常小。类似地，z→–∞导致分母变大使用$\sigma (z)$接近于0。因此，可以总结为sigmoid函数接收实际数值作为输入，将它们转换为[0, 1]之间的值，偏置为$\sigma (0)=0.5$。

为理解逻辑回归模型，我们可以类比第2章。在Adaline中，我们使用了恒等函数$\sigma (z)=z$作为激活函数。在逻辑回归中，这一激活函数变成了我们前面所定义的sigmoid函数。

自适应感知神经元与逻辑回归的不同参见下图，其中唯一的不同之处就是激活函数：

图3.3：逻辑回归与自适应感知神经元的对比

然后sigmoid函数的输出会翻译成具体样式属于类1的概率，$\sigma (z)=p(y=1|\mathbf{x};\mathbf{w},b)$，给定了特征x，并且通过权重w和偏置b进行参数化。例如，假如我们对具体样本花计算$\sigma (z)=0.8$，它表示样本是Iris-versicolor的概率是80%。因此，这朵花是Iris-setosa的概率可计算为$p(y=0|\mathbf{x};\mathbf{w},b)=1-p(y=1|\mathbf{x};\mathbf{w},b)=0.2$，或20%。

预测的概率可通过阈值函数转换为二元输出：

$$\{\begin{array}{ll}1& if\sigma (z)\ge 0.5\\ 0& otherwise\end{array}$$

上图中的sigmoid函数等价于：

$$\{\begin{array}{ll}1& ifz\ge 0.0\\ 0& otherwise\end{array}$$

事实上，很多应用不仅对所预测的类标签感兴趣，而且类标签概率的评估也极为有用（应阈值函数前的sigmoid函数输出）。比如逻辑回归用于天气预报，不仅预测某一天是否下雨，还报告下雨的可能性。类似地，逻辑回归可用于预测有特定症状的病人患某种疾病的概率，这也是为什么逻辑回归在医药行业有很高的知名度。

通过逻辑损失函数学习模型权重

我们已经学习到可以通过逻辑回归模型预测概率和类标签，下面来简单讨论下如何拟合模型的参数，比如权重w和偏置单元b。上一章中我们定义了一个如下的方差损失函数：

$$L(w,b|x)=\sum _i{\frac{1}{2}(\sigma (z^{(i)})-y^{(i)})}^2$$

我们对函数进行了最小化以学习Adaline分类标签的参数。为讲解如何通过逻辑回归获取损失函数，我先定义似然$\mathcal{L}$，假设数据集中的样本彼此并不关联，我们会希望构建一个逻辑回归模型使其最大化。公式如下：

$$\mathcal{L}(w,b|x)=p(y|x;w,b)=\prod _{i=1}^{n}p(y^{(i)}|x^{(i)};w,b)=\prod _{i=1}^n(\sigma (z^{(i)}){)}^{y^{(i)}}(1-\sigma (z^{(i)}){)}^{1-y^{(i)}}$$

在实操中，最大化该等式的（自然）对数会更容易，称之为对数似然方程：

$$l(w,b|x)=\log \mathcal{L}(w,b|x)=\sum _{i=1}[y^{(i)}\log (\sigma (z^{(i)}))+(1-y^{(i)})\log (1-\sigma (z^{(i)}))]$$
首先，应用对数函数会降低数据下溢的可能性，在似然较小时容易产生下溢。其次，我们可以将因子的乘积转换为因子的加和，如果读者还能记得微积分的知识的话，这样可通过加法技巧使用对该函数求导更容易。

推导似然函数

对给定数据$\mathcal{L}(w,b|x)$，我们可以像下面这样获取模型的似然表达式。假设有一个二分类问题，类标签为0和1，可以把标签1看成是伯努利变量-它接收两个值0和1，概率p为1：$Y\sim Bern(p)$。对于单个数据点，可以将概率写成$P(Y=1|X=x^{(i)})=\sigma (z^{(i)})$及$P(Y=0|X=x^{(i)})=1-\sigma (z^{(i)})$。

合并这两个表达式，并使用简写$P(Y=y^{(i)}|X=x^{(i)})=p(y^{(i)}|x^{(i)})$，我们得到了伯努利变量的概率质量函数：

$$p(y^{(i)}|x^{(i)})=(\sigma (z^{(i)}){)}^{y^{(i)}}(1-\sigma (z^{(i)}){)}^{1-y^{(i)}}$$

假如所有训练样本彼此独立我们可以写出训练标签的似然，使用乘法法则来计算所有事件发生的概率，如下：

$$\mathcal{L}(w,b|x)=\prod _{i=1}^{n}p(y^{(i)}|x^{(i)};w,b)$$

这时，替换伯努利变量的概率质量函数，我们就得到了似然表达式，尝试最大化模型参数的变化：

$$\mathcal{L}(w,b|x)=\prod _{i=1}^n(\sigma (z^{(i)}){)}^{y^{(i)}}(1-\sigma (z^{(i)}){)}^{1-y^{(i)}}$$

现在，我们可以使用梯度提升（gradient ascent）等优化算法来最大化该对数似然函数。（梯度提升与第2章中的梯度下降完全一样，只是梯度提升是将最小化替换为最大化函数。）我们这里将对数似然重写为损失函数，L，可使用第2章中的梯度下降实现最小化：

$$L(w,b)=\sum _{i=1}^n[-y^{(i)}\log (\sigma (z^{(i)}))-(1-y^{(i)})\log (1-\sigma (z^{(i)}))]$$

为更好的掌握损失函数，我们来看我们为单训练样本所计算的损失：

$$L(\sigma (z),y;w,b)=-y\log (\sigma (z))-(1-y)\log (1-\sigma (z))$$

从等式可以看出在如果y = 0则第一项为零，y = 1时第二项为零：

$$L(\sigma (z),y;w,b)=\{\begin{array}{ll}-\log (\sigma (z))& \text{if y = 1}\\ -\log (1-\sigma (z))& \text{if y = 0}\end{array}$$

我们来写一个简短的代码脚本创建一张描绘分类针对$\sigma (z)$不同值的分类单训练样本损失的图：

>>> def loss_1(z):
...     return - np.log(sigmoid(z))
>>> def loss_0(z):
...     return - np.log(1 - sigmoid(z))
>>> z = np.arange(-10, 10, 0.1)
>>> sigma_z = sigmoid(z)
>>> c1 = [loss_1(x) for x in z]
>>> plt.plot(sigma_z, c1, label='L(w, b) if y=1')
>>> c0 = [loss_0(x) for x in z]
>>> plt.plot(sigma_z, c0, linestyle='--', label='L(w, b) if y=0')
>>> plt.ylim(0.0, 5.1)
>>> plt.xlim([0, 1])
>>> plt.xlabel('$\sigma(z)$')
>>> plt.ylabel('L(w, b)')
>>> plt.legend(loc='best')
>>> plt.tight_layout()
>>> plt.show()

绘出的图为范围在0到1之间x轴上sigmoid激活（对sigmoid函数的输入为在范围在-10到10之间的z值）以及y轴上关联的逻辑损失：

图3.4：使用逻辑回归的损失函数图

可以看到如果我们正确预测样本属于类1时损失接近0（实线）。类似地，可以看到在正确预测y = 0时y轴的损失接近于0（虚线）。但如果预测错误，损失会趋向无穷大。我们惩罚错误预测的要点是增大损失。

将Adaline 实现转化为逻辑回归算法

如果我们自己实现逻辑回归，可以将第2章中自适应线性神经网络实现的损失函数L替换为新的损失函数：

$$L(w,b)=\frac{1}{n}\sum _{i=1}^n[-y^{(i)}\log (\sigma (z^{(i)}))-(1-y^{(i)})\log (1-\sigma (z^{(i)}))]$$

我们使用它计算每次迭代分类所有训练样本的损失。我们还需要将线性激活函数换成sigmoid。如对Adaline代码做出这些修改，就会得到一个可运行的逻辑回归实现。以下是对全批量梯度下降的实现（但注意也可对随机梯度下降版本做同样的修改）：

class LogisticRegressionGD:
    """Gradient descent-based logistic regression classifier.
    Parameters
    ------------
    eta : float
      Learning rate (between 0.0 and 1.0)
    n_iter : int
      Passes over the training dataset.
    random_state : int
      Random number generator seed for random weight
      initialization.
    Attributes
    -----------
    w_ : 1d-array
      Weights after training.
    b_ : Scalar
      Bias unit after fitting.
    losses_ : list
      Mean squared error loss function values in each epoch.
    """
    def __init__(self, eta=0.01, n_iter=50, random_state=1):
        self.eta = eta
        self.n_iter = n_iter
        self.random_state = random_state
    def fit(self, X, y):
        """ Fit training data.
        Parameters
        ----------
        X : {array-like}, shape = [n_examples, n_features]
          Training vectors, where n_examples is the 
          number of examples and n_features is the 
          number of features.
        y : array-like, shape = [n_examples]
          Target values.
        Returns
        -------
        self : Instance of LogisticRegressionGD
        """
        rgen = np.random.RandomState(self.random_state)
        self.w_ = rgen.normal(loc=0.0, scale=0.01, size=X.shape[1])
        self.b_ = np.float_(0.)
        self.losses_ = []
        for i in range(self.n_iter):
            net_input = self.net_input(X)
            output = self.activation(net_input)
            errors = (y - output)
            self.w_ += self.eta * 2.0 * X.T.dot(errors) / X.shape[0]
            self.b_ += self.eta * 2.0 * errors.mean()
            loss = (-y.dot(np.log(output))
                   - ((1 - y).dot(np.log(1 - output)))
                    / X.shape[0])
            self.losses_.append(loss)
        return self
    def net_input(self, X):
        """Calculate net input"""
        return np.dot(X, self.w_) + self.b_
    def activation(self, z):
        """Compute logistic sigmoid activation"""
        return 1. / (1. + np.exp(-np.clip(z, -250, 250)))
    def predict(self, X):
        """Return class label after unit step"""
        return np.where(self.activation(self.net_input(X)) >= 0.5, 1, 0)

在拟合逻辑回归模型时，我们让铭记它只对二元分类任务有效。

因此我们只考虑山鸢尾和变色鸢尾（类0和1）并检查我产的逻辑回归实现是否有效：

>>> X_train_01_subset = X_train_std[(y_train == 0) | (y_train == 1)]
>>> y_train_01_subset = y_train[(y_train == 0) | (y_train == 1)]
>>> lrgd = LogisticRegressionGD(eta=0.3,
...                             n_iter=1000,
...                             random_state=1)
>>> lrgd.fit(X_train_01_subset,
...          y_train_01_subset)
>>> plot_decision_regions(X=X_train_01_subset,
...                       y=y_train_01_subset,
...                       classifier=lrgd)
>>> plt.xlabel('Petal length [standardized]')
>>> plt.ylabel('Petal width [standardized]')
>>> plt.legend(loc='upper left')
>>> plt.tight_layout()
>>> plt.show()

得到的决策区域图如下：

图3.5：逻辑回归模型的决策区域图

针对逻辑回归的梯度下降学习算法

如果对比LogisticRegressionGD与此前第2章中AdalineGD的代码，可能会注意权重和偏置规则保持不变（除了对第2个因子的缩放）。使用微积分，可以展示通过梯度下降的参数更新与逻辑回归和Adaline确实很像。但请注意下面对梯度下降学习规则的推导是为那些对逻辑回归梯度下降学习规则背后的数学概念感兴趣的读者准备的。不了解不会影响本章后续的学习。

图3.6总结了如何计算对数似然函数对第j个参数的偏导数：

图3.6：计算对数似然函数的偏导数

这里为简洁起见省略了对训练样本求平均。

第2章中我们采取了相反方向的梯度。因此调换了$\frac{\partial L}{w_j}=-(y-a)x_j$并像下面这样更新了第 j个权重，包括学习率$\eta$:

$$w_j:=w_j+\eta (y-a)x_j$$

虽然没有显示出损失函数对偏置的偏导数，使用链式法则的偏置推导整体概念一致，产生了如下的更新规则：

$$b:=b+\eta (y-a)$$

权重及偏置单元的更新与第2章中的自适应线性神经网络一致。

使用scikit-learn训练逻辑回归模型

我们在前面的小节学习了一些有用的代码和数学练习，这有助于我们理解Adaline与逻辑回归概念上的不同。现在我们来学习使用scikit-learn对逻辑回归更优化的实现，它还内置支持多类别配置。请注意在scikit-learn的新版本中，用于多类别、多项因子或OvR的技术，是自动选择的。在下面的代码示例中，我们会使用sklearn.linear_model.LogisticRegressio类以及熟悉的fit方法训练标准化花训练样本中所有三个类别的模型。同时，我们为方便绘图设置了multi_class='ovr'。作为练习，读者可以使用multi_class='multinomial'来比较结果。multinomial配置现在是scikit-learn的LogisticRegression类的默认选择并且在实践中也是互斥类的推荐选项，鸢尾花数据集就属于这种情况。这里的“互斥”表示每个训练样本只能属于一个分类（在多标签分类中，训练样本可以是多个分类的成员）。

下面我们来看示例代码：

>>> from sklearn.linear_model import LogisticRegression
>>> lr = LogisticRegression(C=100.0, solver='lbfgs',
...                         multi_class='ovr')
>>> lr.fit(X_train_std, y_train)
>>> plot_decision_regions(X_combined_std,
...                       y_combined,
...                       classifier=lr,
...                       test_idx=range(105, 150))
>>> plt.xlabel('Petal length [standardized]')
>>> plt.ylabel('Petal width [standardized]')
>>> plt.legend(loc='upper left')
>>> plt.tight_layout()
>>> plt.show()

在对训练数据拟合模型后，我们绘制了决策区域、训练样本和测试样本，如图3.7所示：

图3.7：scikit-learn多类逻辑回归模型的决策区域

凸优化算法

现存有很多算法可解决优化问题。为最小化凸损失函数，比如逻辑回归损失，推荐使用比普通的随机梯度下降 (SGD)更高级的方法。事实上，scikit-learn实现了非常多的这类算法，可通过solver参指定，其中有'newton-cg'、'lbfgs'、'``liblinear'、'sag'和'saga'。

虽然逻辑回归损失是凸损失，但大部分算法应该都可以轻松对全局最小损失收敛。然后，使用其中一些算法相对另一些有某些优势。比如，在之前的版本中（如v 0.21），scikit-learn默认使用'liblinear'，它无法多项损失（multinomial loss），仅限于针对多类分类的OvR模式。但在scikit-learn v 0.22中将默认算法改为了'lbfgs'，表示内存限定Broyden–Fletcher–Goldfarb–Shanno (BFGS)算法(https://en.wikipedia.org/wiki/Limited-memory_BFGS) ，在这方面要更为灵活。

来看前面我们用于训练LogisticRegression模型代码，读者可能会想，“神秘的参数C是什么？”我们会在下一小节中讨论这一参数，其中会介绍过拟合与正则化的概念。但在进行这些讨论之前，先完成对类成员概率的讨论。

训练样本属于某一类的概率可使用predict_proba方法计算。例如，我们可以这样预测测试集前三个样本的概率：

>>> lr.predict_proba(X_test_std[:3, :])

这段代码返回如下数组：

array([[3.81527885e-09, 1.44792866e-01, 8.55207131e-01],
       [8.34020679e-01, 1.65979321e-01, 3.25737138e-13],
       [8.48831425e-01, 1.51168575e-01, 2.62277619e-14]])

第一行对应第一朵花的类成员概率，第二行对应第二朵花的类成员概率，以此类推。各行列的加和是1。（可以通过执行lr.predict_proba(X_test_std[:3, :]).sum(axis=1)来进行确认。）

第一行的最高值大约是0.85，表示对第一个样本属于类3(Iris-virginica) 预测的概率是85%。读者可能已经注意到，我们可以通过找到每行中的最大列来预测类标签，比如使用NumPy的argmax函数：

>>> lr.predict_proba(X_test_std[:3, :]).argmax(axis=1)

返回的类标签如下所示（分别对应Iris-virginica、Iris-setosa和Iris-setosa）：

array([2, 0, 0])

在上面的示例代码中，我们计算了条件概率并手动使用NumPy的argmax函数将它们转化为类标签。实操中，使用scikit-learn获取类标签更便捷的方式是直接调用predict方法：

>>> lr.predict(X_test_std[:3, :])
array([2, 0, 0])

最后，如果希望预测单个花样本的类标签需要注意：scikit-learn接收的数据输入是二维数组，因此，我们需要将单行切片先转化为这种格式。将单行输入转化为二维数组的一种方式是使用NumPy的reshape方法来添加一维，如下所示：

>>> lr.predict(X_test_std[0, :].reshape(1, -1))
array([2])

通过正则化处理过拟合

过拟合是机器学习中一种常见问题，这时模型对训练数据表现很好但对于未知数据（测试数据）的归纳不好。如果模型出现了过拟合，我们还会说模型的方差很高，这可是由参数过多产生的，导致模型对于给定的底层数据过于复杂。类似地，模型也可能会出现欠拟合（高偏差），这表示模型不够复杂未能很好地提取训练数据中的模式，因此对未知数据的表现不佳。

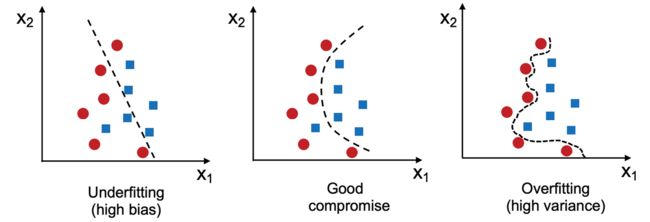
虽然我们还只遇到了线性分类模型，但过拟合和欠拟合的问题可通过比较线性决策边界与更复杂的非线性决策边界来更好的描绘，如图3.8所示：

图3.8：欠拟合、良好拟合和过拟合模型示例

偏差-方差均衡

通常研究人员使用“偏差”和“方差”或“偏差-方差均衡”来描述模型的性能，也就是说读者在演讲、书或文章中可能会碰到说模型是“高方差”或“高偏差”的。那这是什么意思呢？一般我们会说“高方差”与过拟合成正比，而“高偏差”与欠拟合成正比。

在机器学习模型的上下文中，方差度量如果多次重新训练模型时对某一样本分类的模型预测的一致性（或可变性），比如对训练集的不同子集进行训练。我们可以说模型对训练数据中随机性是敏感的。相反，偏差度量在对不同训练数据集多次重建模型时预测距正确值总体有多远，偏差是一种与随机性无关的系统误差的度量。

如果对“偏差”和“方差”的技术细节和推荐感兴趣的话，作者写过相关的授课笔记：https://sebastianraschka.com/pdf/lecture-notes/stat451fs20/08-model-eval-1-intro__notes.pdf。

一种发现好的偏差-方差均衡的方式是通过正则化调优模型的复杂度。正则对于处理共线性（特征高度关联）、过滤数据噪声及最终防止过拟合是一种非常有用的方法。

正则化背后的概念是引入了额外的信息来惩罚极端参数（权重）值。正则化最常见的形式称L2正则化（有时也称为L2收缩或权重衰减），可以写成下面这样：

$$\frac{\lambda }{2n}\Vert w{\Vert }^2=\frac{\lambda }{2n}\sum _{j=1}^m{w}_j^2$$

这里的$\lambda$称为正则化参数。分母里的2只是一个缩放因子，这样在计算损失梯度时约去。类似损失添加了样本大小 n来缩放正则项。

正则化和特征归一化

正则化是标准化这样的特征缩放很重要的另一个原因。为让正则化正常动作，我们需要保障所有的特征在可比较的量级上。

逻辑回归的损失函数可通过添加简单正则项来正则化，正则项会在模型训练时收缩权重：

$$L(w,b)=\frac{1}{n}\sum _{i=1}^n[-y^{(i)}\log (\sigma (z^{(i)}))-(1-y^{(i)})\log (1-\sigma (z^{(i)}))]+\frac{\lambda }{2n}\Vert w{\Vert }^2$$

未正则化的偏导数定义为：

$$\frac{\partial L(w,b)}{\partial w_j}=(\frac{1}{n}\sum _{i=1}^n(\sigma (w^T{x}^{(i)})-y^{(i)})x_j^{(i)})$$

对损失添加正则项会将这一偏导数变成如下的形式：

$$\frac{\partial L(w,b)}{\partial w_j}=(\frac{1}{n}\sum _{i=1}^n(\sigma (w^T{x}^{(i)})-y^{(i)})x_j^{(i)})+\frac{\lambda }{n}{w}_j$$

通过正则化参数，$\lambda$，我们可以控制拟合训练数据的紧密程度，同时也保持权重很小。通过增大$\lambda$的值，我们增加了正则化强度。请注意第2章中学习过的偏置单元，基本是截距项或负阈值，通常不做正则化。

scikit-learn中为LogisticRegression类实现的参数C，源自支持向量机的约定，这是下一节中的话题。C项与正则化参数$\lambda$成反比。因此，减少其值可会翻转正则化参数C，也即增加正则化的强度，可通过绘制有两个权重系数的L2正则化路径来进行可视化：

>>> weights, params = [], []
>>> for c in np.arange(-5, 5):
...     lr = LogisticRegression(C=10.**c,
...                             multi_class='ovr')
...     lr.fit(X_train_std, y_train)
...     weights.append(lr.coef_[1])
...     params.append(10.**c)
>>> weights = np.array(weights)
>>> plt.plot(params, weights[:, 0],
...          label='Petal length')
>>> plt.plot(params, weights[:, 1], linestyle='--',
...          label='Petal width')
>>> plt.ylabel('Weight coefficient')
>>> plt.xlabel('C')
>>> plt.legend(loc='upper left')
>>> plt.xscale('log')
>>> plt.show()

通过执行以上代码，我们使用用于翻转正则化参数C的不同值拟合了10个逻辑回归模型。为便于绘图，我们只收集了类1（这里是数据集中的第二个类：Iris-versicolor）对所有分类器的权重系数，还记得我们使用OvR技术来进行多类分类吧。

可以通过输出图看出，如果减小参数C也即增加正则化强度则权重系数收缩：

图3.9：翻转L2正则化模型结果上的正则化强度参数C的影响

增加正则化强度会减小过拟合，那么读者可能会问为什么不默认对所有模型进行强正则化呢？原因是在调整正则化强度时也格外小心。例如，如果正则化强度过高而权重系统接近于零，模型会因欠拟合而表现很差，参见图3.8。

有关逻辑回归的其它资源

因为对单独分类算法的深入讲解不在本书的范畴内，推荐希望更深入了解逻辑回归的读者阅读，逻辑回归:从入门到高级概念和应用，Dr. Scott Menard，塞奇出版公司，2009年。