C语言初阶——函数part2

目录

六.一个小补充

七.函数的嵌套

八.函数的链式访问

九.函数的声明和定义

1.理解声明和定义

2.声明定义的用法

（1）代码的分工

（2）代码的隐藏

 3.对比变量的声明和定义

十.函数的递归

1.递归的定义

2.最简单的递归 

 3.深度理解

（1）按照顺序打印一个整数的每一位

 （2）两个关键

（3）再举个例子

十一.函数的递归和迭代

1.递归和迭代的对比

2.解决方法

3.三个提示

 结束语

---

我们接着上节的来说

六.一个小补充

我们看一个函数里面，到底需要不需要return

我们在输入的时候，希望我们输入的几个数据，需要返回的时候，这个时候函数里需要来定义接收

当我们需要他返回的时候，我们加上return，然后主函数里也要接收返回的值

当我们不返回的时候，就加上void，当我们不要参数的时候，就加上void

返回什么类型的函数，我们就要定义函数是什么类型的

如果我们不加void，C语言中默认就是int 类型

int test(void)
{
	printf("hehe\n");
}

int main()
{
	int ret = test();
	printf("%d\n", ret);

	return 0;
}

七.函数的嵌套

#include 

void new_line()
{
	printf("hehe\n");
}
void three_line()
{
	int i = 0;
	for (i = 0; i < 3; i++)
	{
		new_line();
	}
}
int main()
{
	three_line();
	return 0;
}

特别注意的：函数可以嵌套调用，不可以嵌套定义

八.函数的链式访问

 把一个函数的返回值作为另一个函数的参数

#include 

int main()
{
	//int len = strlen("abcdef");
	printf("%d\n", strlen("abcdef"));//这地方把strlen("abcdef")这个函数的返回值当中printf的参数了

	return 0;
}

int main()
{
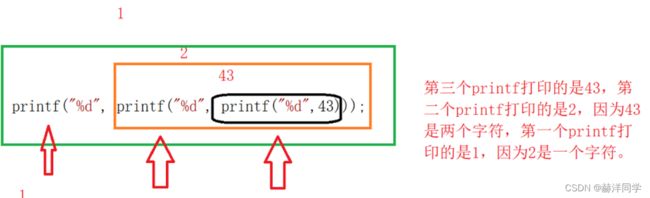
	printf("%d", printf("%d", printf("%d", 43)));

	return 0;
}

就是把strlen("abcdef")这个函数的返回值当中printf的参数了

我们再来看经典printf

#include 
int main()
{
	printf("%d", printf("%d", printf("%d", 43)));//从里往外看
	//第一个printf打印的是43，然后是两个字符，到第二个printf中，两个字符打印2，变成一个字符了，第三个printf打印1，结果4321.
	//结果是啥？
	//注：printf函数的返回值是打印在屏幕上字符的个数
	return 0;
}

注：printf函数的返回值是打印在屏幕上字符的个数

九.函数的声明和定义

1.理解声明和定义

1.声明：告诉编译器有一个函数叫什么，参数是什么，返回类型是什么。但是具体是不是存在，函数声明决定不了。

函数的声明一般出现在函数的使用之前。要满足先声明后使用。

函数的声明一般要放在头文件中的。

2.定义：函数的定义是指函数的具体实现，交待函数的功能实现。

int Add(int x, int y);

int main()
{
	int a = 0;
	int b = 0;
	scanf("%d %d", &a, &b);
	//求和
	int ret = Add(a, b);
	printf("%d\n", ret);

	return 0;
}

//函数的定义
//函数的定义也是一种特殊的声明
int Add(int x, int y)
{
	return x + y;
}

当我们没有第一行的声明的时候，就会报错，只有定义没有声明

所以我们把函数主体都放在main后的时候，就会报错，因为函数没有声明，所以必须在前面声明，在后面定义可以

我们平常写的时候，就直接把声明和定义都放在前面了

2.声明定义的用法

（1）代码的分工

我们写个计算器

加法——a代码

减法——b代码

乘法——c代码

除法——d代码

可以四个人来写，每个人写自己的模块，然后写个测试模块，合到一起就行

我们头文件add.c放

#pragma once
//后面会学上面这个

int Add(int x, int y);
//声明我放到头文件里面来

 源文件add.c放

#define _CRT_SECURE_NO_WARNINGS 1

int Add(int x, int y)
{
	return x + y;
}
//函数的定义放到源文件里面来

源文件test.c放 

//声明我放到头文件里面来
//函数的定义放到源文件里面来
//所以这里我们就这样调用就可以了
#include "add.h"

//add.h和add.c这俩是加法模块，前面放的函数的声明，后面放的是函数的实现
//test.c是测试模块，你想用的话，包含一下我的头文件#include "add.h"
//跟库函数差不多的意思，这里是我们自己写的，用双引号来引，库里面的用<>

int main()
{
	int a = 0;
	int b = 0;
	scanf("%d %d", &a, &b);
	int ret = Add(a, b);
	printf("%d\n", ret);

	return 0;
}

add.h和add.c这俩是加法模块，前面放的函数的声明，后面放的是函数的实现
test.c是测试模块，你想用的话，包含一下我的头文件#include "add.h"
跟库函数差不多的意思，这里是我们自己写的，用双引号来引，库里面的用<>

（2）代码的隐藏

当没有头文件的时候，我们两个源文件，用extern来声明就行extern int Add(int x, int y);

静态库，我们只简单了解一下

所以我们给我们创建的变成静态库

点属性点常规点配置类型，改成静态库，找到lib后缀的文件，就是我们的静态库

静态库我们看的时候打不开的，记事本打开也看不到

我们卖的时候，就把这个lib静态库，卖走，然后把头文件也卖了，只能看见函数的声明

我们使用的时候，需要导入静态库

#pragma comment(lib, "add.lib")

这样就能正常使用了，lib里面放的是函数的定义，别人看不见

 3.对比变量的声明和定义

也都是一样的道理

int g_val = 2022;

//变量的定义
int g_val = 2022;

//这个时候是定义，有定义的时候，前面出现的是声明，没有定义的时候，这个就是定义
int val;//这个就是定义
全局变量不初始化的时候，默认是0
int main()
{
	printf("%d\n", val);//所以我们就打印出来是0
	return 0;
}

十.函数的递归

1.递归的定义

程序调用自身的编程技巧称为递归（ recursion）。

递归做为一种算法在程序设计语言中广泛应用。 一个过程或函数在其定义或说明中有直接或间接调用自身的

一种方法，它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解，

递归策略

只需少量的程序就可描述出解题过程所需要的多次重复计算，大大地减少了程序的代码量。

递归的主要思考方式在于：把大事化小

只需少量的程序就可描述解题过程中所需要的多次重复计算，大大地减少了程序的代码量

2.最简单的递归 

函数内部自己调用自己，就叫递归，无限套娃，最后会自己崩掉，叫栈溢出

int main()
{
	printf("hehe\n");
	main();

	return 0;
}

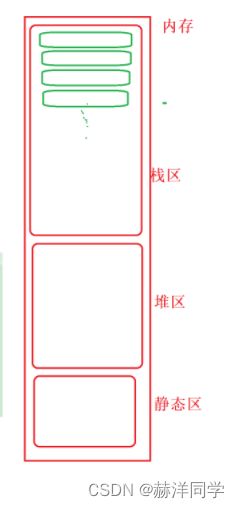
每一次调用函数都会为本次函数，在内存的栈区上开辟一块内存空间

越来越多，我们把栈区空间消耗完了，栈溢出

 3.深度理解

（1）按照顺序打印一个整数的每一位

例如：

输入：1234，输出 1 2 3 4.

我们先分析一下

1234 % 10 = 4 得到4

123 / 10 = 123 把4去掉

123 % 10 = 3 得到3

123 / 10 = 12 去掉3

12 % 10 = 2 得到2

12 / 10 = 1 去掉2

1 % 10 = 1 得到1

1 / 10 = 0 结束

但是这样是倒着打印的

我们代码实现

void Print(unsigned int n)
{
	while (n)//最后变成0就截止，当成出循环条件每次往里面传
	{
		printf("%d ", n % 10);
		n = n / 10;
	}
}
int main()
{
	unsigned int num = 0;//定义一个无符号的值
	scanf("%u", &num);
	//写一个函数打印num的每一位
	Print(num);
	return 0;
}

我们用递归来分析

刚才用print(1234)

我们用print(123) 然后打印4

还能分为print(12) 然后打印3 4

还能分为print(1) 然后打印2 3 4

就是

print(n)

print(n / 10)      printf("%d", n % 10);

代码实现

void Print(unsigned int n)
{
	if (n > 9)
	{
		Print(n/10);
	}
	printf("%d ", n % 10);
}

int main()
{
	unsigned int num = 0;
	scanf("%u", &num);
	//写一个函数打印num的每一位
	Print(num);
	return 0;
}

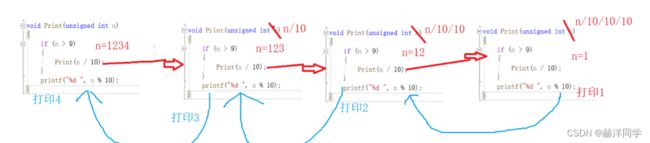
递归是递推和回归

我们输入1234

1234 > 9, 我们进入到了print这个函数里面，此时没有打印，

我们的n进入到第二个print函数中，n = 123了

123 > 9, 我们进入到了print这个函数里面，此时没有打印，

我们的n进入到第三个print函数中，n = 12了

12 > 9, 我们进入到了print这个函数里面，此时没有打印，

我们的n进入到第四个print函数中，n = 1了

1 > 9, 这个时候就不成立，不进入了，我们就开始打印了

直到我们不能在递归的时候，开始往回传值

我们上去的时候，是n % 10

最里一层 1 % 10 打印1

往外 12 % 10 打印2

再往外 123 % 10 打印3

最外一层 1234 % 4 打印4

打印1，回到上个print中来打印2，再回到上一个print打印3，再回到上一个print打印4

层层递进，然后回归值

 （2）两个关键

存在限制条件，当满足这个限制条件的时候，递归便不再继续。

每次递归调用之后越来越接近这个限制条件。

（3）再举个例子

 编写函数不允许创建临时变量，求字符串的长度。

先做个铺垫，求字符串长度

#include 

int main()
{
	char arr[] = "bit";
	int len = strlen(arr);
	printf("%d\n", len);

	return 0;
}

但是题目的要求，让我们自己写个函数来求，不能用库函数，我们先不用递归来写

int my_strlen(char* str)//参数怎么写字符指针，下面传来的是b的地址，数组首元素的地址
{
	int count = 0;
	while (*str != '\0')
	{
		count++;
		str++;//字符指针+1，向后跳1个字符
	}
	return count;
}
int main()
{
	char arr[] = "bit";
	//[b i t \0]
	//数组名其实是数组首元素的地址
	//我们传arr的时候，传的是b的地址，b是一个字符，所以我们上面接收要用字符指针
	int len = my_strlen(arr);
	printf("%d\n", len);

	return 0;
}

数字符串的时候，数到\0

b i t \0

str指向我的b

* str != '\0'//*str 就是我的字符，看他等于不等于\0，不等于的时候就是一个字符，就加一个

count++

str++ //然后要把指针往后走，判断下一个,所以需要一个循环

整型指针+1，往后跳一个整型

  我们用递归来写

思路

my_strlen("bit");

1 + my_strlen("it");

1 + my_strlen("t");

1 + my_strlen("");

最后这个就是\0,就不往下了

#include 
#include 

int my_strlen(char* str)
{
	if (*str != '\0')
		return 1 + my_strlen(str + 1);
	else
		return 0;
}

int main()
{
	char arr[] = "bit";
	int len = my_strlen(arr);
	printf("%d\n", len);

	return 0;
}

1 + my_strlen(str + 1);

str + 1就是往下一个字符的地址

我们来看bit

我们第一个进入的是b，b != \0, 我们进入到return 1 + my_strlen(str + 1);

此时没有返回，我们的str + 1，现在进入到第二个函数里

i != \0,我们进入到return 1 + my_strlen(str + 1);

此时没有返回，我们的str + 1，现在进入到第三个函数里

t != \0, 我们进入到return 1 + my_strlen(str + 1);

此时没有返回，我们的str + 1，现在进入到第四个函数里

\0 != \0, 不成立了，就开始返回了

返回到第三个里面my_strlen(str + 1)为0，第三个变为return 1;

返回到第二个里面my_strlen(str + 1)为1，第二个变为return 2;

返回到第一个里面my_strlen(str + 1)为2，第一个变为return 3;

我们输出结果为3

 

十一.函数的递归和迭代

1.递归和迭代的对比

我们用例子来看，求n的阶乘

思路：

n != n!*(n - 1)!
n! = 1   n<=1
n! = n!*(n - 1)    n>2

代码实现

int factorial(int n)
{
    if (n <= 1)
        return 1;
    else
        return n * factorial(n - 1);
}

上面使用递归写的，但是当数非常大的时候，会直接崩掉，但是我们用迭代来写，很大的时候，返回的结果虽然不对，但是不会崩掉，迭代大概就是循环的意思

我们用迭代来写

int factorial(int n)
{
    int result = 1;
    while (n > 1)
    {
        result *= n;
        n -= 1;
    }
    return result;
}

虽然计算很大的数的时候，程序给的结果可能不对，但是程序不会崩掉 

我们再来看个例子，我们再看求第n个斐波那契数

思路：

这个就是兔子数列
1 1 2 3  5 8 13 21 34 55 第三个数是前两个的和

代码实现

int fib(int n)
{
    if (n <= 2)
        return 1;
    else
        return fib(n - 1) + fib(n - 2);
}

 在使用 fib 这个函数的时候如果我们要计算第50个斐波那契数字的时候特别耗费时间

我们写个count来看一下第三个数被重复计算了多少次

int count = 0;//全局变量
int fib(int n)
{
    if (n == 3)
        count++;
    if (n <= 2)
        return 1;
    else
        return fib(n - 1) + fib(n - 2);
}

我们发现 fib 函数在调用的过程中很多计算其实在一直重复，最后我们输出看看count，是一个很大很大的值，太多的重复计算了，程序就会崩掉，我们用迭代来写就不会出现

栈溢出:

在调试 factorial 函数的时候，如果你的参数比较大，那就会报错： stack overflow（栈溢出）这样的信息。
系统分配给程序的栈空间是有限的，但是如果出现了死循环，或者（死递归），这样有可能导致一直开辟栈空间，最终产生栈空间耗尽的情况，这样的现象我们称为栈溢出。

我们用迭代来写

思路：

a    b     c       
1    1     2
1    2     3
2    3     5
    c = a + b;
        a = b;
        b = c;

int Fib(int n)
{
	int a = 1;
	int b = 1;
	int c = 1;
	while (n>2)
	{
		c = a + b;
		a = b;
		b = c;
		n--;
	}
	return c;
}

这样就会很快的计算完，也没有很多的重复计算

2.解决方法

1. 将递归改写成非递归。
2. 使用static对象替代 nonstatic 局部对象。在递归函数设计中，可以使用 static 对象替代
nonstatic 局部对象（即栈对象），这不仅可以减少每次递归调用和返回时产生和释放 nonstatic 对象的开销，而且 static 对象还可以保存递归调用的中间状态，并且可为各个调用层所访问。

大概解释一下第二条，把本来放在栈区里的局部变量，放在改为静态区里，这样一定程度上，来缓解内存的压力。

3.三个提示

1. 许多问题是以递归的形式进行解释的，这只是因为它比非递归的形式更为清晰。
2. 但是这些问题的迭代实现往往比递归实现效率更高，虽然代码的可读性稍微差些。
3. 当一个问题相当复杂，难以用迭代实现时，此时递归实现的简洁性便可以补偿它所带来的运行时开
销。

 结束语

这节课基本上把函数讲完了，我们下节课会仔细的讲栈帧，还有几个递归中很经典的问题，加油！