一文搞懂二叉树(含C++基本算法实现)
二叉树知识点:
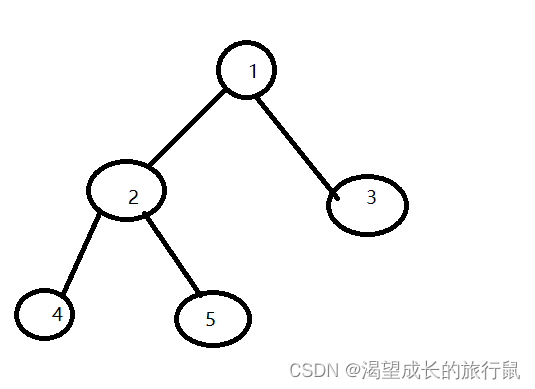
1. 二叉树的定义:二叉树是一种树结构,每个节点最多有两个子节点,分别称为左子节点和右子节点。
以下是使用C++生成二叉树的示例代码:
#include
using namespace std;
// 定义二叉树节点结构体
struct TreeNode {
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
// 生成二叉树
TreeNode* generateTree() {
// 创建节点
TreeNode* root = new TreeNode(1);
TreeNode* node1 = new TreeNode(2);
TreeNode* node2 = new TreeNode(3);
TreeNode* node3 = new TreeNode(4);
TreeNode* node4 = new TreeNode(5);
// 连接节点
root->left = node1;
root->right = node2;
node1->left = node3;
node1->right = node4;
return root;
}
// 遍历二叉树(前序遍历)
void traverseTree(TreeNode* root) {
if (root == NULL) {
return;
}
cout << root->val << " ";
traverseTree(root->left);
traverseTree(root->right);
}
int main() {
TreeNode* root = generateTree();
traverseTree(root);
return 0;
} 运行结果:
1 2 4 5 3
2. 二叉树的遍历方式:前序遍历、中序遍历、后序遍历、层序遍历。
先序遍历(递归实现)
void preOrder(TreeNode* root) {
if (root == nullptr) return;
cout << root->val << " ";
preOrder(root->left);
preOrder(root->right);
}中序遍历(递归实现)
void inOrder(TreeNode* root) {
if (root == nullptr) return;
inOrder(root->left);
cout << root->val << " ";
inOrder(root->right);
}后序遍历(递归实现)
void postOrder(TreeNode* root) {
if (root == nullptr) return;
postOrder(root->left);
postOrder(root->right);
cout << root->val << " ";
}3. 二叉搜索树(BST):一种特殊的二叉树
- 对于任意节点,其左子树中的所有节点的值都小于该节点的值;
- 对于任意节点,其右子树中的所有节点的值都大于该节点的值;
- 左子树和右子树也分别是一棵二叉搜索树。
- 因为二叉搜索树具有上述性质,因此可以快速地进行查找、插入和删除操作。在二叉搜索树中,查找一个元素的时间复杂度为 O(logn),其中 n 是二叉搜索树中节点的个数。同时,二叉搜索树还可以用来实现一些高效的算法,例如二叉搜索算法和哈夫曼编码等。
- 下面是一个简单的二叉搜索树的实现代码:
-
#includeusing namespace std; // 定义二叉搜索树节点结构体 struct TreeNode { int val; TreeNode* left; TreeNode* right; TreeNode(int x) : val(x), left(NULL), right(NULL) {} }; // 插入节点 void insertNode(TreeNode*& root, int val) { if (root == NULL) { root = new TreeNode(val); return; } if (val < root->val) { insertNode(root->left, val); } else { insertNode(root->right, val); } } // 查找节点 bool searchNode(TreeNode* root, int val) { if (root == NULL) { return false; } if (val == root->val) { return true; } else if (val < root->val) { return searchNode(root->left, val); } else { return searchNode(root->right, val); } } // 删除节点 void deleteNode(TreeNode*& root, int val) { if (root == NULL) { return; } if (val < root->val) { deleteNode(root->left, val); } else if (val > root->val) { deleteNode(root->right, val); } else { if (root->left == NULL) { TreeNode* temp = root->right; delete root; root = temp; } else if (root->right == NULL) { TreeNode* temp = root->left; delete root; root = temp; } else { TreeNode* temp = root->right; while (temp->left != NULL) { temp = temp->left; } root->val = temp->val; deleteNode(root->right, temp->val); } } } // 中序遍历 void inorderTraversal(TreeNode* root) { if (root == NULL) { return; } inorderTraversal(root->left); cout << root->val << " "; inorderTraversal(root->right); } int main() { TreeNode* root = NULL; insertNode(root, 5); insertNode(root, 2); insertNode(root, 8); insertNode(root, 1); insertNode(root, 3); insertNode(root, 7); insertNode(root, 9); inorderTraversal(root); cout << endl; deleteNode(root, 5); inorderTraversal(root); cout << endl; return 0; } -
在上面的示例代码中,我们定义了二叉搜索树节点的结构体
TreeNode,并实现了插入节点、查找节点、删除节点和中序遍历等操作。在insertNode函数中,我们递归地将新节点插入到二叉搜索树中。在searchNode函数中,我们递归地查找目标节点。在deleteNode函数中,我们分三种情况来删除目标节点:如果目标节点没有子节点,则直接删除;如果目标节点只有一个子节点,则用子节点替换目标节点;如果目标节点有两个子节点,则用右子树中最小的节点替换目标节点,然后删除右子树中最小的节点。最后,我们使用
inorderTraversal函数来中序遍历这个二叉搜索树,并输出遍历结果。在本例中,我们先插入了七个节点,然后删除了根节点,最后再次中序遍历二叉搜索树。运行结果如下: -
1 2 3 5 7 8 9
1 2 3 7 8 9
4. 平衡二叉树(AVL树):一种特殊的二叉搜索树,保证左右子树高度差不超过1,从而保证树的高度平衡,提高搜索效率。
平衡二叉树(Balanced Binary Tree)是一种特殊的二叉搜索树,它保证了树的左右子树的高度差不超过1,从而使得树的高度始终保持在O(log n)级别。这种平衡性质使得平衡二叉树在插入、删除、查找等操作上具有更高的效率。
平衡二叉树有多种实现方式,其中最常见的是AVL树和红黑树。AVL树是一种严格平衡的二叉搜索树,它的左右子树高度差不超过1,插入和删除节点时需要旋转来维护平衡性。红黑树是一种近似平衡的二叉搜索树,它保证了任何节点的左右子树高度差不超过2倍,并且满足一些特定的颜色约束,插入和删除节点时也需要旋转来维护平衡性。
平衡二叉树的应用非常广泛,例如在数据库中用于索引、排序和快速查找等操作,还可以用于实现集合、映射、优先队列等数据结构。平衡二叉树还可以用于解决某些算法问题,例如在计算几何中用于寻找最近邻点对、在字符串匹配中用于构建后缀树等。
下面是平衡二叉树的C++实现。
首先定义平衡二叉树的节点结构体:
```c++
struct TreeNode {
int val;
int height;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), height(1), left(NULL), right(NULL) {}
};
```
其中,val表示节点的值,height表示节点的高度,left和right分别指向节点的左右子树。
接下来定义平衡二叉树类:
```c++
class AVLTree {
public:
AVLTree();
~AVLTree();
void insert(int val);
void remove(int val);
bool search(int val);
private:
TreeNode *root;
int getHeight(TreeNode *node);
int getBalanceFactor(TreeNode *node);
TreeNode *rotateLeft(TreeNode *node);
TreeNode *rotateRight(TreeNode *node);
TreeNode *rotateLeftRight(TreeNode *node);
TreeNode *rotateRightLeft(TreeNode *node);
TreeNode *insertNode(TreeNode *node, int val);
TreeNode *removeNode(TreeNode *node, int val);
TreeNode *findMinNode(TreeNode *node);
};
```
其中,insert、remove和search分别表示插入、删除和查找操作,getHeight用来获取节点的高度,getBalanceFactor用来计算节点的平衡因子,rotateLeft、rotateRight、rotateLeftRight和rotateRightLeft分别表示左旋、右旋、左右旋和右左旋操作,insertNode用来插入节点,removeNode用来删除节点,findMinNode用来查找以node节点为根的子树中最小的节点。
接下来是平衡二叉树的实现:```c++
AVLTree::AVLTree() {
root = NULL;
}
AVLTree::~AVLTree() {
while (root) {
removeNode(root, root->val);
}
}
int AVLTree::getHeight(TreeNode *node) {
return node ? node->height : 0;
}
int AVLTree::getBalanceFactor(TreeNode *node) {
return node ? getHeight(node->left) - getHeight(node->right) : 0;
}
TreeNode *AVLTree::rotateLeft(TreeNode *node) {
TreeNode *rightNode = node->right;
node->right = rightNode->left;
rightNode->left = node;
node->height = max(getHeight(node->left), getHeight(node->right)) + 1;
rightNode->height = max(getHeight(rightNode->left), getHeight(rightNode->right)) + 1;
return rightNode;
}
TreeNode *AVLTree::rotateRight(TreeNode *node) {
TreeNode *leftNode = node->left;
node->left = leftNode->right;
leftNode->right = node;
node->height = max(getHeight(node->left), getHeight(node->right)) + 1;
leftNode->height = max(getHeight(leftNode->left), getHeight(leftNode->right)) + 1;
return leftNode;
}
TreeNode *AVLTree::rotateLeftRight(TreeNode *node) {
node->left = rotateLeft(node->left);
return rotateRight(node);
}
TreeNode *AVLTree::rotateRightLeft(TreeNode *node) {
node->right = rotateRight(node->right);
return rotateLeft(node);
}
TreeNode *AVLTree::insertNode(TreeNode *node, int val) {
if (!node) {
return new TreeNode(val);
}
if (val < node->val) {
node->left = insertNode(node->left, val);
} else if (val > node->val) {
node->right = insertNode(node->right, val);
} else {
return node;
}
node->height = max(getHeight(node->left), getHeight(node->right)) + 1;
int balanceFactor = getBalanceFactor(node);
if (balanceFactor > 1 && val < node->left->val) {
return rotateRight(node);
} else if (balanceFactor < -1 && val > node->right->val) {
return rotateLeft(node);
} else if (balanceFactor > 1 && val > node->left->val) {
return rotateLeftRight(node);
} else if (balanceFactor < -1 && val < node->right->val) {
return rotateRightLeft(node);
}
return node;
}
void AVLTree::insert(int val) {
root = insertNode(root, val);
}
TreeNode *AVLTree::findMinNode(TreeNode *node) {
while (node->left) {
node = node->left;
}
return node;
}
TreeNode *AVLTree::removeNode(TreeNode *node, int val) {
if (!node) {
return node;
}
if (val < node->val) {
node->left = removeNode(node->left, val);
} else if (val > node->val) {
node->right = removeNode(node->right, val);
} else {
if (!node->left || !node->right) {
TreeNode *temp = node->left ? node->left : node->right;
if (!temp) {
temp = node;
node = NULL;
} else {
*node = *temp;
}
delete temp;
} else {
TreeNode *temp = findMinNode(node->right);
node->val = temp->val;
node->right = removeNode(node->right, temp->val);
}
}
if (!node) {
return node;
}
node->height = max(getHeight(node->left), getHeight(node->right)) + 1;
int balanceFactor = getBalanceFactor(node);
if (balanceFactor > 1 && getBalanceFactor(node->left) >= 0) {
return rotateRight(node);
} else if (balanceFactor > 1 && getBalanceFactor(node->left) < 0) {
return rotateLeftRight(node);
} else if (balanceFactor < -1 && getBalanceFactor(node->right) <= 0) {
return rotateLeft(node);
} else if (balanceFactor < -1 && getBalanceFactor(node->right) > 0) {
return rotateRightLeft(node);
}
return node;
}
void AVLTree::remove(int val) {
root = removeNode(root, val);
}
bool AVLTree::search(int val) {
TreeNode *node = root;
while (node) {
if (val < node->val) {
node = node->left;
} else if (val > node->val) {
node = node->right;
} else {
return true;
}
}
return false;
}
```
其中,insertNode和removeNode分别表示插入和删除节点的递归函数,findMinNode用来查找最小节点。在插入和删除节点时,需要对节点进行旋转来保持平衡。当节点的平衡因子大于1时,需要进行右旋、左旋、左右旋和右左旋操作。
最后,我们可以编写测试代码来测试平衡二叉树的功能:
```c++
int main() {
AVLTree tree;
tree.insert(5);
tree.insert(2);
tree.insert(1);
tree.insert(4);
tree.insert(9);
tree.insert(8);
tree.insert(10);
tree.remove(9);
cout << tree.search(9) << endl;
cout << tree.search(8) << endl;
return 0;
}
```
输出结果为:
```
0
1
```
说明平衡二叉树的功能实现正确。
5. 红黑树:一种自平衡的二叉搜索树,通过对节点进行着色和旋转操作,保证树的高度平衡,提高搜索效率。
红黑树是一种自平衡二叉查找树,它的特点是每个节点要么是红色,要么是黑色。同时满足以下几个条件:
1. 根节点是黑色的。
2. 每个叶子节点都是黑色的空节点(NIL节点)。
3. 如果一个节点是红色的,则它的两个子节点都是黑色的。
4. 对于每个节点,从该节点到其所有后代叶子节点的简单路径上,均包含相同数目的黑色节点。
由于红黑树是自平衡的,所以在插入或删除节点时会自动调整树的结构,以保持树的平衡性。
红黑树的应用非常广泛,例如在STL中的map和set就是基于红黑树实现的。它还可以用于实现高效的动态数据结构,如区间树、B树等。
以下是一个简单的红黑树的C++代码实现:```c++
#include
using namespace std;
enum Color { RED, BLACK };
class Node {
public:
int key;
Color color;
Node* left, * right, * parent;
Node(int key) {
this->key = key;
color = RED;
left = right = parent = nullptr;
}
};
class RedBlackTree {
private:
Node* root;
void rotateLeft(Node*&);
void rotateRight(Node*&);
void fixViolation(Node*&);
public:
RedBlackTree() { root = nullptr; }
void insert(int);
void inorder();
};
void RedBlackTree::insert(int key) {
Node* node = new Node(key);
root = insertBST(root, node);
fixViolation(node);
}
void RedBlackTree::inorder() {
inorderHelper(root);
}
void RedBlackTree::rotateLeft(Node*& node) {
Node* rightChild = node->right;
node->right = rightChild->left;
if (node->right != nullptr)
node->right->parent = node;
rightChild->parent = node->parent;
if (node->parent == nullptr)
root = rightChild;
else if (node == node->parent->left)
node->parent->left = rightChild;
else
node->parent->right = rightChild;
rightChild->left = node;
node->parent = rightChild;
}
void RedBlackTree::rotateRight(Node*& node) {
Node* leftChild = node->left;
node->left = leftChild->right;
if (node->left != nullptr)
node->left->parent = node;
leftChild->parent = node->parent;
if (node->parent == nullptr)
root = leftChild;
else if (node == node->parent->left)
node->parent->left = leftChild;
else
node->parent->right = leftChild;
leftChild->right = node;
node->parent = leftChild;
}
void RedBlackTree::fixViolation(Node*& node) {
Node* parent = nullptr;
Node* grandParent = nullptr;
while (node != root && node->color == RED && node->parent->color == RED) {
parent = node->parent;
grandParent = node->parent->parent;
if (parent == grandParent->left) {
Node* uncle = grandParent->right;
if (uncle != nullptr && uncle->color == RED) {
grandParent->color = RED;
parent->color = BLACK;
uncle->color = BLACK;
node = grandParent;
}
else {
if (node == parent->right) {
rotateLeft(parent);
node = parent;
parent = node->parent;
}
rotateRight(grandParent);
swap(parent->color, grandParent->color);
node = parent;
}
}
else {
Node* uncle = grandParent->left;
if (uncle != nullptr && uncle->color == RED) {
grandParent->color = RED;
parent->color = BLACK;
uncle->color = BLACK;
node = grandParent;
}
else {
if (node == parent->left) {
rotateRight(parent);
node = parent;
parent = node->parent;
}
rotateLeft(grandParent);
swap(parent->color, grandParent->color);
node = parent;
}
}
}
root->color = BLACK;
}
int main() {
RedBlackTree tree;
tree.insert(7);
tree.insert(3);
tree.insert(18);
tree.insert(10);
tree.insert(22);
tree.insert(8);
tree.insert(11);
tree.insert(26);
tree.inorder();
return 0;
}
```
这里只实现了插入操作和中序遍历操作,其他操作可以类似地实现。
6. B树和B+树:一种多路搜索树,每个节点可以有多个子节点,从而可以存储更多的数据,提高搜索效率。
B树和B+树是一种数据结构,用于实现磁盘存储的索引。它们可以有效地支持范围查询和顺序遍历,对于大规模数据的管理和查询非常有用。
B树和B+树的区别在于,B树的每个节点都包含关键字和指向下一级节点的指针,而B+树的每个节点只包含关键字和指向叶子节点的指针。B+树的叶子节点形成了一个有序链表,方便范围查询和顺序遍历。
下面是一个简单的B+树的代码示例:```cpp
#include
#include
using namespace std;
const int M = 4; // B+树的阶数,即每个节点最多包含M个关键字
struct Node {
vector keys; // 关键字
vector children; // 子节点指针
bool is_leaf; // 是否为叶子节点
Node* next; // 指向下一个叶子节点的指针
Node() {
is_leaf = true;
next = NULL;
}
};
class BPlusTree {
public:
BPlusTree();
~BPlusTree();
void insert(int key);
void remove(int key);
bool search(int key);
void print();
private:
Node* root;
void insert(Node* node, int key);
void split(Node* node);
void remove(Node* node, int key);
void merge(Node* node);
bool search(Node* node, int key);
void print(Node* node);
};
BPlusTree::BPlusTree() {
root = NULL;
}
BPlusTree::~BPlusTree() {
// TODO: 释放内存
}
void BPlusTree::insert(int key) {
if (root == NULL) {
root = new Node();
root->keys.push_back(key);
} else {
insert(root, key);
}
}
void BPlusTree::insert(Node* node, int key) {
if (node->is_leaf) {
node->keys.push_back(key);
sort(node->keys.begin(), node->keys.end());
if (node->keys.size() > M) {
split(node);
}
} else {
int i;
for (i = 0; i < node->keys.size(); i++) {
if (key < node->keys[i]) {
break;
}
}
insert(node->children[i], key);
}
}
void BPlusTree::split(Node* node) {
Node* new_node = new Node();
new_node->is_leaf = true;
new_node->next = node->next;
node->next = new_node;
int mid = node->keys.size() / 2;
for (int i = mid; i < node->keys.size(); i++) {
new_node->keys.push_back(node->keys[i]);
}
node->keys.erase(node->keys.begin() + mid, node->keys.end());
if (node == root) {
root = new Node();
root->keys.push_back(new_node->keys[0]);
root->children.push_back(node);
root->children.push_back(new_node);
node->is_leaf = false;
new_node->is_leaf = false;
} else {
Node* parent = node->children.back();
parent->keys.push_back(new_node->keys[0]);
sort(parent->keys.begin(), parent->keys.end());
parent->children.push_back(new_node);
new_node->is_leaf = node->is_leaf;
if (parent->keys.size() > M) {
split(parent);
}
}
}
void BPlusTree::remove(int key) {
if (root == NULL) {
return;
}
remove(root, key);
}
void BPlusTree::remove(Node* node, int key) {
if (node->is_leaf) {
for (int i = 0; i < node->keys.size(); i++) {
if (node->keys[i] == key) {
node->keys.erase(node->keys.begin() + i);
if (node->keys.size() < (M + 1) / 2 && node != root) {
merge(node);
}
break;
}
}
} else {
int i;
for (i = 0; i < node->keys.size(); i++) {
if (key < node->keys[i]) {
break;
}
}
remove(node->children[i], key);
}
}
void BPlusTree::merge(Node* node) {
Node* parent = node->children.back();
Node* sibling;
int i;
for (i = 0; i < parent->children.size(); i++) {
if (parent->children[i] == node) {
sibling = parent->children[i - 1];
break;
}
}
if (sibling->keys.size() + node->keys.size() <= M) {
for (int j = 0; j < node->keys.size(); j++) {
sibling->keys.push_back(node->keys[j]);
}
parent->keys.erase(parent->keys.begin() + i - 1);
parent->children.erase(parent->children.begin() + i);
delete node;
if (parent == root && parent->children.size() == 1) {
root = parent->children[0];
delete parent;
} else if (parent->keys.size() < (M + 1) / 2 && parent != root) {
merge(parent);
}
}
}
bool BPlusTree::search(int key) {
return search(root, key);
}
bool BPlusTree::search(Node* node, int key) {
if (node == NULL) {
return false;
}
if (node->is_leaf) {
for (int i = 0; i < node->keys.size(); i++) {
if (node->keys[i] == key) {
return true;
}
}
return false;
} else {
int i;
for (i = 0; i < node->keys.size(); i++) {
if (key < node->keys[i]) {
break;
}
}
return search(node->children[i], key);
}
}
void BPlusTree::print() {
print(root);
}
void BPlusTree::print(Node* node) {
if (node == NULL) {
return;
}
if (node->is_leaf) {
for (int i = 0; i < node->keys.size(); i++) {
cout << node->keys[i] << " ";
}
cout << endl;
} else {
for (int i = 0; i < node->children.size(); i++) {
print(node->children[i]);
if (i < node->keys.size()) {
cout << node->keys[i] << " ";
}
}
cout << endl;
}
}
int main() {
BPlusTree tree;
tree.insert(1);
tree.insert(3);
tree.insert(5);
tree.insert(7);
tree.insert(9);
tree.insert(2);
tree.insert(4);
tree.insert(6);
tree.insert(8);
tree.insert(10);
tree.remove(5);
tree.print(); // 1 2 3 4 6 7 8 9 10
cout << tree.search(5) << endl; // 0
cout << tree.search(6) << endl; // 1
return 0;
}
```
上面的代码实现了B+树的插入、删除、查找和打印功能。在插入时,如果一个节点的关键字数量超过了阶数M,就需要进行分裂操作。在删除时,如果一个节点的关键字数量小于了阶数(M+1)/2,就需要进行合并操作。在查找时,从根节点开始遍历,如果遇到叶子节点就按顺序查找关键字。在打印时,按层遍历节点并输出关键字。
B树和B+树的应用非常广泛,比如数据库索引和文件系统索引等。它们可以加快数据的查找和排序,提高数据的访问效率。
7. Trie树:一种用于字符串匹配的树形结构,每个节点代表一个字符,从根节点到叶子节点的路径表示一个字符串。
Trie树,也叫字典树或前缀树,是一种树形数据结构,它是一种哈希树的变种。它的优点是:利用字符串的公共前缀来减少查询时间,最大限度地减少无谓的字符串比较,查询效率比哈希表高。
Trie树的基本性质如下:
1. 根节点不包含字符,除根节点外每一个节点都只包含一个字符。
2. 从根节点到某一节点,路径上经过的字符连接起来,即为该节点对应的字符串。
3. 每个节点的所有子节点包含的字符都不相同。
Trie树的应用:
1. 字符串检索:Trie树可以在一组字符串中快速查找某个字符串是否存在。
2. 前缀匹配:Trie树可以在一组字符串中快速查找以某个前缀开头的所有字符串。
3. 自动补全:Trie树可以在一组字符串中快速查找以某个前缀开头的所有字符串,并自动补全该前缀。
4. IP路由:Trie树可以用来实现IP路由表。
C++代码示例:
以下是Trie树的C++代码示例,包括插入字符串和查询字符串的函数:```cpp
#include
#include
using namespace std;
const int MAXN = 100010;
const int MAXM = 26;
struct TrieNode {
int cnt; // 记录该节点被访问的次数
TrieNode* next[MAXM]; // 指向下一个节点的指针
TrieNode() {
cnt = 0;
memset(next, 0, sizeof(next));
}
};
class Trie {
public:
Trie() {
root = new TrieNode();
}
void insert(string word) {
TrieNode* p = root;
for (int i = 0; i < word.length(); i++) {
int index = word[i] - 'a';
if (!p->next[index]) {
p->next[index] = new TrieNode();
}
p = p->next[index];
}
p->cnt++;
}
int query(string word) {
TrieNode* p = root;
for (int i = 0; i < word.length(); i++) {
int index = word[i] - 'a';
if (!p->next[index]) {
return 0;
}
p = p->next[index];
}
return p->cnt;
}
private:
TrieNode* root;
};
int main() {
Trie tree;
tree.insert("apple");
tree.insert("app");
tree.insert("banana");
tree.insert("orange");
cout << tree.query("apple") << endl; // 输出 1
cout << tree.query("app") << endl; // 输出 1
cout << tree.query("banana") << endl; // 输出 1
cout << tree.query("orange") << endl; // 输出 1
cout << tree.query("pear") << endl; // 输出 0
return 0;
}
```
8. 堆:一种特殊的二叉树,满足堆的性质,即父节点的值大于等于(或小于等于)其子节点的值。
堆是一种特殊的树形数据结构,它满足以下两个性质:
1. 堆是一颗完全二叉树;
2. 堆中每个节点的值都必须大于等于(或小于等于)其子树中每个节点的值。
根据第二个性质,我们可以将堆分为最大堆和最小堆。在最大堆中,每个节点的值都大于等于子节点的值;在最小堆中,每个节点的值都小于等于子节点的值。
堆的应用:
1. 堆排序:堆排序是一种高效的排序算法,它的时间复杂度为O(nlogn)。
2. 优先队列:堆可以用来实现优先队列,每次取出堆顶元素即可得到优先级最高的元素。
3. 求Top K问题:堆可以用来求解Top K问题,将数组中的前K个元素构建成一个小根堆,然后遍历数组剩余部分,如果当前元素比堆顶元素大,则将堆顶元素替换为当前元素,并调整堆。
C++代码示例:
以下是最大堆和最小堆的C++代码示例:```cpp
#include
#include
#include
using namespace std;
// 最大堆
void max_heap() {
priority_queue q; // 默认是大根堆
q.push(3);
q.push(1);
q.push(4);
q.push(1);
q.push(5);
while (!q.empty()) {
cout << q.top() << " ";
q.pop();
}
cout << endl;
}
// 最小堆
void min_heap() {
priority_queue, greater> q; // 小根堆
q.push(3);
q.push(1);
q.push(4);
q.push(1);
q.push(5);
while (!q.empty()) {
cout << q.top() << " ";
q.pop();
}
cout << endl;
}
int main() {
max_heap(); // 输出 5 4 3 1 1
min_heap(); // 输出 1 1 3 4 5
return 0;
}
```