二叉树的建立，输出，深度，宽度与最大宽度，节点总数，叶子节点数，删除，c/c++描述

  内容来自课本例题。通过总结，学得才更深入，才更便于记忆。
  二叉树的建立，函数createBTree，课本采用栈的方法，和二叉树的逗号表达式是匹配的。详细分析，见上篇
  二叉树的输出，函数displayBTree，采用递归方法，遇到子节点，则开始输出左括号。详细见上篇。
  二叉树的深度：函数depthBiTree，其递归定义是左右子节点的较大深度加1.这也是该函数的编程思想，空节点深度为0，无子节点的节点深度为1。
  查找二叉树里某一节点，函数findNode，返回指向该节点的指针。递归思路是，空节点返回null，若根节点即是要找的节点，返回根节点，否则返回根节点的左右两棵子树的查找信息。因为二叉树里每一个节点，既是其祖先节点的子节点，也是其自身子孙节点的根节点，即自身树 的根节点。所有节点数据结构都是相同的。
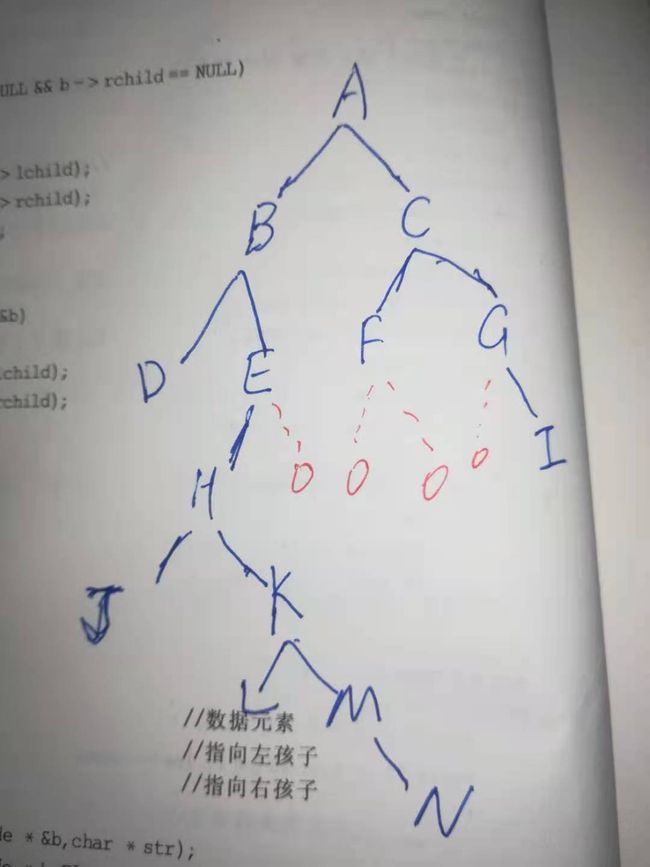
  二叉树的宽度与最大宽度：函数widthBiTree。宽度定义是二叉树的拥有最多节点的那一行包含的节点数，这里指的节点都是非空节点。最大宽度定义是当包含左右两端节点之间空节点时的行的最大宽度。我们明白其中所指 的区别即可。举例如下：

  其宽度是第三行的3，最大宽度就是第三行的4，包含了一个空节点。我就是看了bilibili网站up主“动画讲编程”的队列演示，理解了二叉树的层序遍历是怎么进行。 剩下的思路就好办了。b栈up主的视频地址如下（读者们也去跟着这位up主好好学学，就不用看我在这里逼逼了，最核心的入门问题，人家帮咱们解决了）：
https://www.bilibili.com/video/BV16f4y1B7KN?t=620

  我这不算侵犯人家版权，我只是截图了人家劳动成果，还给人家推广分享了。请求理解。我自己手画同样的图，也没有人家做的好啊，我不必要刻意追求原创，自己的原创没人家的好。而且想跟有缘的读者分享最关键的知识。所以截了人家仅仅一张图。说不定人家up主还不说我侵犯版权，还要谢谢我的分享与阅读呢，有缘的读者咱们也要理解啊，谢谢。
  求宽度还是有难度的。因为二叉树的链式存储结构，存储的是纵向父母节点与子女节点之间的指向关系，最容易求的是深度。对于节点的同一行的兄弟节点、堂兄弟节点，到底有多少个，在哪里，真的不能从二叉树的链接关系上直接反映出来。咱们人类肉眼可以直接观察出来，电脑可不会这么未卜先知，神通广大。这里用到了队列，队列有保存功能，把节点数据存储在队列里自己的数组成员里，这里采用顺序队列，非链式队列。因为这样直接访问队列里的数组更方便。存取更方便用数组，插入删除更快捷用链表。
  总结求解思路一句话就是：假如入队列了某一行所有节点，也就知晓了该行的宽度，即节点个数，那么这行元素依次出队列，根据该行的节点信息，我们完全能确定其下一行所有节点的信息，比如宽度和最大宽度，并将这下一行的所有非空节点入队列。根据这下一行的 节点信息，我们完全可以确定下下一行的节点信息。换言之，我们把需要的上一行的节点信息都存入队列数组，再访问队列数组，我们就可以确定本行所有节点的信息，包括本行的宽度与最大宽度。从根节点开始，依次循环，直至访问完二叉树的所有行。
  至此，求解每行宽度已经非常明朗了。如何求解最大宽度呢？关键是确定最左和最右两端节点的位置，中间的空节点也要计数。程序里我们采用了一个逻辑标志布尔量bool start，c++里有这个数据类型，c语言里可以用1 和0 分别表示逻辑真和假，检测到下一行第一个非空节点后，start =true，从此本行出队的每一个非空节点的子节点，都对变量int countWidth加1，对应其两个子节点，总共加2，不管其两个子节点是否为空。直至出队完本行所有元素。当然下一行的最右端元素，可能在偏中间一些，不一定是本行最后一个出队元素的右子节点，也就是说不一定是本行最右端元素的右子节点。下一行最右端节点再往右的空节点，不是我们要统计入最大宽度的。这里引入了一个方法是变量int countNull，统计下一行中的空子节点的数目，遇到非空节点则清零。这样本行最后一个非空子节点后的空子节点数目会保存在这个变量中，不会被清零，countWidth - countNull ，两值相减，就得到了下一行的最大宽度。程序也是按这个思路写的。结果也正确。反正课本里的代码我是没看懂。课本代码如下，仍然很感谢课本，内容很全面。我们不过是在老师肩上才看得更远。

  二叉树的总节点数：，函数totalNodesOfBiTree。其递归定义是根节点的左右两棵子树的总节点数之和加1.1指的是根节点本身占了1。空树的节点数为0.
  二叉树的叶子节点数：函数numberOfLeafNodes。其递归定义是根节点的左右两棵子树的叶子节点数之和。空树的叶子节点数为0，没有子节点的根节点，叶子节点数为1.递归思路，也是编程思路，具体代码记不住，记住思路就好。
  二叉树的删除：函数destroy。递归思路是，空节点什么也不做return，叶子节点直接删除叶子节点，否则删除根节点的左右子节点后，再删除这个根节点。


  先粘贴main函数所在源文件代码：

#include
#include
using namespace std;
#define STACKDEPTH 15
struct BiTreeNode {
	char value;
	BiTreeNode* leftChild;
	BiTreeNode* rightChild;
};
extern void createBTree(BiTreeNode*& bTreeRoot, char*& ptChar);
extern void displayBTree(BiTreeNode*& bTreeRoot);
extern BiTreeNode* findNode(BiTreeNode *& biTreeRoot,char m);
extern BiTreeNode* leftChildNode(BiTreeNode *& parentNode);
extern BiTreeNode* rightChildNode(BiTreeNode*& parentNode);
extern int depthBiTree(BiTreeNode*& biTreeRoot);
extern int widthBiTree(BiTreeNode*& biTreeRoot);
extern int totalNodesOfBiTree(BiTreeNode*& biTreeRoot);
extern int numberOfLeafNodes(BiTreeNode*& biTreeRoot);
extern void destroy(BiTreeNode*& biTreeRoot);


int main() {
	char array[] = "A(B(D,E(H(J,K(L,M(,N))))),C(F,G(,I)))";
	char* ptChar = array;  //c++里只能这样分开定义，要不会出错。
	BiTreeNode* bTreeRoot = NULL;

	createBTree(bTreeRoot,ptChar);
	cout << "the char array is :";
	for (int i = 0; array[i] != '\0'; i++)
		cout << array[i];
	cout<< endl<< "binary tree is    :";
	displayBTree(bTreeRoot);
	cout << endl;

	BiTreeNode* ptNode = findNode(bTreeRoot,'K');
	if (ptNode != NULL) {
		cout << "node 'K' : ";
		BiTreeNode* pt = leftChildNode(ptNode);
		if (pt != NULL)
			cout << "left child is " << pt->value << ',';
		else
			cout << "has no left child node ,";

		pt = rightChildNode(ptNode);
		if (pt != NULL)
			cout << "right child is " << pt->value << '.';
		else
			cout << "has no right child node .";
	}

	cout << endl << "binary tree depth : " << depthBiTree(bTreeRoot);
	cout << endl << "binary tree max width : " << widthBiTree(bTreeRoot)<<endl;
	cout << "total number of binary tree : " << totalNodesOfBiTree(bTreeRoot);
	cout << endl << "number of leaf nodes : " << numberOfLeafNodes(bTreeRoot);
	cout <<endl <<"destroy binary tree."<<endl;
	destroy(bTreeRoot);
	
	return 0;
}

  接着是main函数调用的所有函数代码，存储在另一个源文件里：

#include
#include
using namespace std;
#define STACKDEPTH 15
#define QUEUELENGTH 20
#define MAXDEPTH 10
struct BiTreeNode {
	char value;
	BiTreeNode* leftChild;
	BiTreeNode* rightChild;
};
void createBTree(BiTreeNode*& bTreeRoot, char*& ptChar) {
	struct {
		BiTreeNode* ptsBiTree[STACKDEPTH];
		int indexTop = -1;
	}sequStack;

	BiTreeNode* ptNew = NULL;
	char s;
	int leftRight;//1 is left   2 is right
	while (*ptChar != '\0') {
		s = *ptChar;
		if ('A' <= s && s <= 'Z') {
			ptNew = new BiTreeNode;
			ptNew->value = s;
			ptNew->leftChild = ptNew->rightChild = NULL;

			if (bTreeRoot == NULL)
				bTreeRoot = ptNew;
			else if (leftRight == 1)
				sequStack.ptsBiTree[sequStack.indexTop]->leftChild = ptNew;
			else if (leftRight == 2)
				sequStack.ptsBiTree[sequStack.indexTop]->rightChild = ptNew;
		}
		else if (s == '(') {
			sequStack.indexTop++;
			sequStack.ptsBiTree[sequStack.indexTop] = ptNew;
			leftRight = 1;
		}
		else if (s == ',')
			leftRight = 2;
		else if (s == ')')
			sequStack.indexTop--;

		ptChar++;
	}
}
void displayBTree(BiTreeNode*& bTreeRoot) {   // 本查找方法是先序遍历
	if (bTreeRoot == NULL)
		return;//if binary tree does not exsit,return
	cout << bTreeRoot->value;
	if (bTreeRoot->leftChild != NULL || bTreeRoot->rightChild != NULL) {
		cout << '(';
		displayBTree(bTreeRoot->leftChild);

		if (bTreeRoot->rightChild != NULL)
			cout << ',';

		displayBTree(bTreeRoot->rightChild);
		cout << ')';
	}
}

BiTreeNode* findNode(BiTreeNode*& biTreeRoot, char m) {
	if (biTreeRoot == NULL)
		return NULL;
	else if (biTreeRoot->value == m)
		return biTreeRoot;
	
	BiTreeNode* pt = findNode(biTreeRoot->leftChild,m);
	if (pt != NULL)
		return pt;
	else
		return findNode(biTreeRoot->rightChild,m);

}
BiTreeNode* leftChildNode(BiTreeNode*& parentNode) {
	return parentNode->leftChild;
}
BiTreeNode* rightChildNode(BiTreeNode*& parentNode) {
	return parentNode->rightChild;
}
int depthBiTree(BiTreeNode*& biTreeRoot) {
	if (biTreeRoot == NULL)
		return 0;
	
	int depthLeft = depthBiTree(biTreeRoot->leftChild);
	int depthRight = depthBiTree(biTreeRoot->rightChild);
	return (depthLeft > depthRight ? depthLeft : depthRight) + 1;
}
int widthBiTree(BiTreeNode*& biTreeRoot) {
	if (biTreeRoot == NULL)  return 0;
	if (biTreeRoot != NULL && biTreeRoot->leftChild == NULL &&
		biTreeRoot->rightChild == NULL)
		return 1;

	int rankNodesNoNull[MAXDEPTH];
	int rankWidth[MAXDEPTH];
	struct {  //this is a circle queue
		BiTreeNode* nodes[QUEUELENGTH];
		int head = 0;
		int tail = 0;
	}queue;
	
	rankWidth[1] = 1;
	rankNodesNoNull[1] = 1;
	queue.tail++;
	queue.nodes[queue.tail] = biTreeRoot;
	
	bool start;
	int countWidth, countNoNull,countNull;
	int maxWidth = 1;
	//countNull是统计空节点的个数，遇真实节点则清零，以统计行宽度
	for (int depth = 1; depth < depthBiTree(biTreeRoot); depth++) {
		start = false; // //下一行的开始，计数的开始标志
		countWidth = countNoNull = countNull = 0;

		for (int i = 1; i <= rankNodesNoNull[depth]; i++) {
			queue.head = (queue.head + 1) % QUEUELENGTH;
			if (queue.nodes[queue.head]->leftChild != NULL) {
				start = true;
				countNull = 0;

				countNoNull++;
				queue.tail = (queue.tail + 1) % QUEUELENGTH;
				queue.nodes[queue.tail] = queue.nodes[queue.head]->leftChild;
			}
			else
				countNull++;
				
			if (start == true) countWidth++;
			
			if (queue.nodes[queue.head]->rightChild != NULL) {
				start = true;
				countNull = 0;
				countNoNull++;

				queue.tail = (queue.tail + 1) % QUEUELENGTH;
				queue.nodes[queue.tail] = queue.nodes[queue.head]->rightChild;
			}
			else
				countNull++;
			if (start == true) countWidth++;
		}
		rankNodesNoNull[depth + 1] = countNoNull;
		rankWidth[depth + 1] = countWidth - countNull;

		if (maxWidth < rankWidth[depth + 1]) 
			maxWidth = rankWidth[depth + 1];
	}
	return maxWidth;
}

int totalNodesOfBiTree(BiTreeNode*& biTreeRoot) {
	//递归方法,非递归方法见上例求最大宽度，用队列可以求解。
	//递归定义是一棵二叉树的总节点数是其左总节点数和右总节点数的和加1
	if (biTreeRoot == NULL)
		return 0;
	if (biTreeRoot->leftChild == NULL && biTreeRoot->rightChild == NULL)
		return 1;
	return totalNodesOfBiTree(biTreeRoot->leftChild) +
		totalNodesOfBiTree(biTreeRoot->rightChild) + 1;
}
int numberOfLeafNodes(BiTreeNode*& biTreeRoot) { 
	if (biTreeRoot == NULL)
		return 0;
	if (biTreeRoot->leftChild == NULL && biTreeRoot->rightChild == NULL)
		return 1;
	return numberOfLeafNodes(biTreeRoot->leftChild) +
		numberOfLeafNodes(biTreeRoot->rightChild);
}
void destroy(BiTreeNode*& biTreeRoot) {
	if (biTreeRoot == NULL)
		return;
	if (biTreeRoot->leftChild != NULL)
		destroy(biTreeRoot->leftChild);
	if (biTreeRoot->rightChild != NULL)
		destroy(biTreeRoot->rightChild);
	delete(biTreeRoot);
}

测试结果如下：

课本里举例的二叉树是这样的，比逗号表达式更直观：

谢谢阅读。