《算法笔记》9.7 堆

9.7 堆

9.7.1 堆的定义与基本操作

堆是一棵完全二叉树，树中每个结点的值都不小于（或不大于）其左右孩子结点的值。其中，如果父亲结点的值大于或等于孩子结点的值，那么称这样的堆为大顶堆，这时，每个结点的值都是以它为根结点的子树的最大值。相反，则为小顶堆。

那么对于一个给定的初始序列，怎样把它建成一个堆呢？

从最后一个元素开始，从下往上，从右往左。假设当前元素X，让x与X的孩子结点比较，如果发现比X更大的元素Y，则交换X与Y的位置，这样Y就成了根结点，而X则成为了孩子结点。交换之后让X继续与其孩子结点比较，直到X的孩子结点都比X小或没有孩子节点为止。

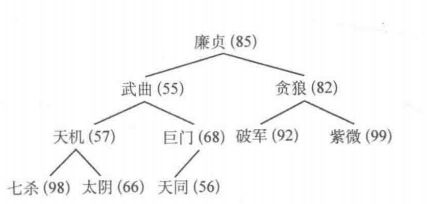
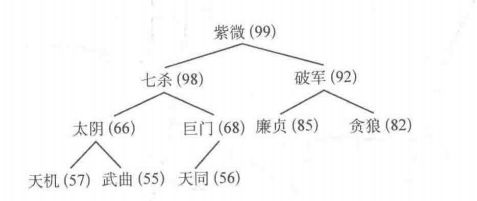
例如:

从下往上，从右往左

• 第一个有孩子结点的是巨门，但是天同比巨门小，不同调整。
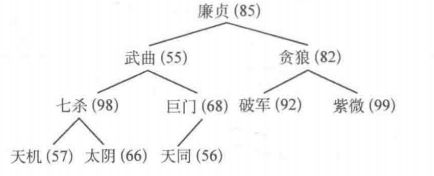
• 天机：七杀比太阴大，天机与七杀相比七杀大，交换七杀与天机的位置。交换后天机没有孩子结点，调整结束。

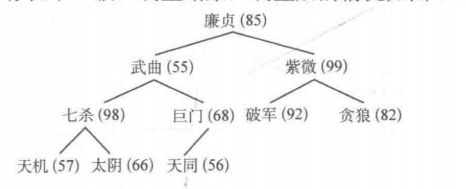
• 贪狼：紫薇比破军大，且比贪狼大，交换贪狼和紫薇。交换后贪狼没有孩子结点，调整结束。

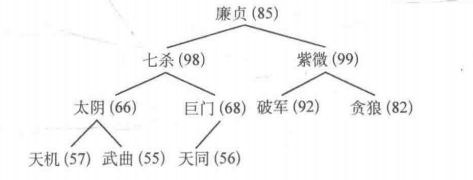
• 武曲：七杀比巨门大，也比武曲大，交换武曲与七杀，交换后武曲有孩子天机和太阴，继续调整。太阴比天机大，也比武曲大，交换武曲与太阴的位置，交换后的武曲没有孩子节点，调整结束。

• 廉贞：紫薇比七杀大，比廉贞大，交换廉贞与紫薇的位置，交换后廉贞有孩子破军和贪狼，继续调整。破军比贪狼，廉贞大，交换廉贞与破军的位置，交换后廉贞没有孩子结点，调整结束。

至此，建堆完成。

那具体是怎么实现的呢，对完全二叉树来说，使用数组存储完全二叉树。这样结点就按层序存储在数组中，其中第一个节点将存储于数组中的1号位，并且数组i号位表示的结点的左孩子是(2i)号位，有孩子则是(2i+1)号位。则可以这样定义数组来表示堆

const int maxn = 100 ;
//head为堆，n为元素个数
int heap[maxn] , n = 10 ;

根据上面建堆的过程，每次调整都是把结点从上往下调整。针对这种向下调整，调整的方法是这样的：总是将当前结点V与它的左右孩子比较（如果有的话），假如孩子中存在比当前结点V权值大的，就将其中权值最大的孩子结点与结点V交换；交换完毕后继续让结点V和孩子比较，直到结点V的孩子的权值都比结点V的权值小或结点V没有孩子结点。

代码如下，时间复杂度为O(logN)：

//对heap数组在[low,high]范围内进行调整
//low为欲调整结点的数组下标，high一般为堆的最后一个元素数组下标
void downAdjust( int low , int high ){
    int i = low , j = 2 * i ;  //i为欲调整结点，j为其左孩子结点
    while( j <= high ){ //存在孩子结点
        //右孩子存在并且比左孩子大
        if( j+1 <= high && heap[j+1] > heap[j] ){
            j = j+1 ;  //j记录右孩子的数组下标
        }
        
        //孩子节点比当前节点大
        if( heap[j] > heap[i] ){
            swap( heap[j] , heap[i] ) ;  //交换两个结点
            i = j ;     //保持i为欲调整结点、j为i的左孩子
            j = 2 * i ;
        }
        else{
            break ;  //孩子结点的权值均比欲调整结点i小，调整结束
        }
    }
    
}

那么建堆的过程就很容易了。假设序列中元素个数为n，由于完全二叉树的叶子节点个数为向上取整(n/2)，因此数组下标在 [ 1 , 向下取整(n/2) ] 范围内的结点都是非叶子结点。于是可以从 向下取整(n/2) 号位开始 倒着 枚举结点，对每个遍历到的结点i进行[i,n]范围内的调整。
为什么要倒着枚举呢？
这是因为每次调整完一个结点后，当前子树中权值最大的结点就会处在根结点的位置，这样当遍历到其父亲节点时，就可以直接使用这个结果。符合从下往上，从右往左的规则

建堆代码如下，时间复杂度位O(N)

//建堆
void createHeap(){
    for( int i = n / 2 ; i >= 1 ; i-- ){
        downAdjust(i , n) ;
    }
}

另外，如果要删除堆中的最大元素（也就是堆顶元素），并让其仍然保持堆的结构，那么只需要将最后一个元素覆盖堆顶元素，然后对根结点进行调整，时间复杂度为O(logN)

//删除堆顶元素
void deleteTop(){
    heap[1] = heap[n--] ;  //用最后一个元素覆盖堆顶元素，并让元素个数减一
    downAdjust(1 , n) ;  //向下调整元素

}

如果想要往堆里添加一个元素，可以把想要添加的元素放在数组最后（也就是完全二叉树的最后一个节点后面），然后进行向上调整。 向上调整总是把欲调整结点与父亲结点比较，如果权值比父亲节点大，那么就交换其与父亲结点，这样反复比较，直到到达顶堆或父亲结点权值较大为止。

//对heap数组在[low,high]范围进行向上调整
//其中low一般设置为1，high表示欲调整结点的数组下标
void upAdjust( int low , int high ){
    int i = high , j = i / 2 ;   //i为欲调整结点，j为其父亲结点
    while( j >= low ){  //存在父亲结点
        if( heap[j] < heap[i] ){    //父亲结点权值小于欲调整结点
            swap( heap[j] , heap[i] ) ; //交换
            i = j ;
            j = i / 2 ;
        }
        else{
            break ;
        }
    }
}

在此基础之上，很容易实现添加元素的代码

//添加元素x
void insert( int x ){
    heap[++n] = x ;   //让元素个数加1，然后将数组末位赋值为x
    upAdjust(1 , n) ;  //向上调整加入的结点n
}

9.7.2 堆排序

堆排序是指使用堆结构对一个序列进行排序。现在讨论递增排序的情况。
考虑对一个堆来说，堆顶元素是最大的，因此在建堆完毕后，堆排序的直观思路就是取出堆顶元素，然后将堆的最后一个元素替换至堆顶，再进行一次针对堆顶元素的向下调整——如此重复，直到堆中只剩下一个元素为止。

//堆排序
void heapSort(){
    createHeap() ; //建堆
    for( int i = n ; i > 1 ; i-- ){ //倒着枚举，直到堆中只有一个元素
        swap( heap[i] , heap[1] ) ; //交换heap[i]与堆顶
        downAdjust(1 , i-1) ;  //调整堆顶