深度优先搜索算法（depth-first-search）

1、基本介绍

地位：是应用最广泛的搜索算法，简称dfs。

基本思想：按照深度优先的方式搜索，通俗来说就是“一条路走到黑”。

本质：dfs是一种穷举（暴力算法）的手段，实际上就是把所有的可行方案列举出来，不断去试探，直到找到问题的解，其过程是对每一个可能的分支路径深入到不能再深入为止，而且每个顶点只能访问一次。

对于算法新手来说，看以上的基本介绍会感到很迷惑，不过没关系，我们可以来举例子。

2、DFS案例引入之迷宫问题基本思路

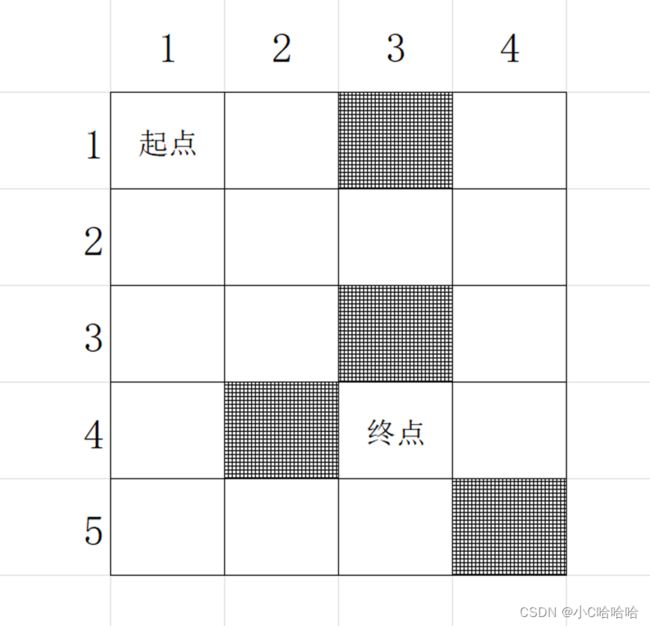
我们以迷宫问题来理解DFS算法的基本思想，比如，有如下这样的一个地图：

场景模拟：假设你是游戏的主人公， 你从起点出发，要求出到达终点的最短路径，假设每走一个格子算一步。那你会如何走迷宫？你可能是这样的：如果你遇到直路，就一直往前走，如果遇到分叉路口，就任意选择其中的一条继续往下走，如果遇到死胡同，就退回到最近的一个分叉路口，选择另一条道路再走下去，如果走到了终点，你就看一下目前走了几步，记录一下，用来和以后另一条路到达终点所经过的步数做比较，以此来求出从起点到终点的最短路径。

对比着以上的场景，我们再来回顾一下DFS的基本思想：按照某种原则往前试探搜索，如果前进中遇到失败（比如你遇到死胡同），则退回头另选通路继续搜索，直到找到满足条件的目标为止。

 我们插入一段小视频来讲解一下DFS思想在迷宫问题当中的应用，有助于大家更好地理解DFS算法。

DFS基本思想讲解

  3、DFS案例引入之迷宫问题代码实现

这部分对于新手来说理解起来可能有困难，你可以结合我第2小节所讲的视频来一一对应理解代码。在编写代码之前，我们先来做约定，假设你在走迷宫的时候是按照右下左上的原则来走的，根据不同的约定原则，具体的代码实现也不一样。

对于每一个坐标而言，在出发时，都是按照右下左上的方式来前进， 在此时，我们需要编写一个递归函数，如果你对递归的知识点不了解，那么往下的内容你就不必再看了，你十分有必要再去学习一下递归的相关知识点，因为要学习DFS算法的前提是需要深刻理解递归的。

从某个位置出发，我们来编写一个函数，不妨叫做dfs()函数，dfs()函数的功能是解决当前应该怎么办，因为我们的目标是要到达终点，因此当你走到某个位置的时候，第一件事情是需要判断一下是否已经到达了终点位置，且看一下当前到达终点所花费的步数是否小于之前到达终点所花费的步数，如果没有到达终点位置，则按照右下左上的原则找到下一步可以走的地方。因此，dfs()的函数声明可以写：

void dfs(int x,int y,int step) {
    
    return;
}

其中，x，y代表当前你已经到达的坐标位置，step代表到达当前位置所花费的步数。

在如上的概述中，有提到：当到达某个位置的时候，应该要判断该点是否为终点且判断一下当前到达终点所花费的步数是否小于之前到达终点所花费的步数，具体代码如下：

void dfs(int x,int y,int step) {
    //判断当前所在的位置是否为终点位置
    if(x==p&&y==q) //(p,q)为终点坐标
    {
        //步数是否比之前到达终点的步数更短
        if(step

如果没有到达终点位置，则找出下一步可以走的地方，对于迷宫问题来说，有四个方向可以走，分别是右、下、左、上。我们先用一个二维的方向数组，来表示从(x,y)位置出发，可能到达的那些点（右、下、左、上）在x坐标和y坐标方向上的增量，如下：

int next[4][2] = {
                    {0,1},  //向右走
                    {1,0},  //向下走
                    {0,-1}, //向左走
                    {-1,0}  //向上走
                };

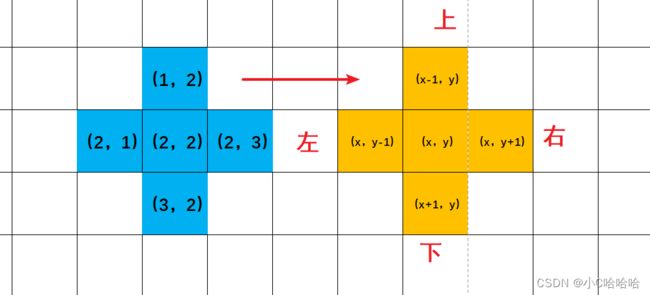
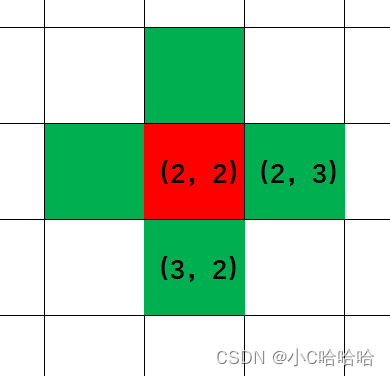
举个例子：比如当前在(2,2)这个位置，那么往右边走就是(2+0,2+1)，到达(2,3)的位置，往下走就是(2+1,2+0)，到达(3,2)的位置

 通过next这个方向数组，使用循环，我们就可以获得到达右、下、左、上这四个方向的增量坐标，具体代码如下：

for(k=0;k<=3;k++) {
    //计算下一个可能到达的点的坐标
    tx = x + next[k][0];
    ty = y + next[k][1];
}

为什么我说(tx,ty)是可能的坐标呢？举个例子，如下图所示，如果当前你从(2,4)的位置走到(1,4)的位置，那么右边和上边已经超出迷宫范围了，越界了，不能走，左边是障碍物，也不能走，下面是刚刚已经走过的，不能再走了。我们发现(1,4)右、下、左、上四个位置都无法到达，因此会回退到(2,4)的位置。

通过以上分析，我们得出，当下一个点(tx,ty)为越界、障碍物、已经走过时，这个点我们就无法到达。因此，我们在for循环内加一层这样的判断：

for(k=0;k<=3;k++) {
    //计算下一个可能的坐标
    tx = x + next[k][0];
    ty = y + next[k][1];

    //判断该点是否越界 
    if(tx < 1 || tx > n || ty < 1 || ty > m) {
        //强制进入下一轮循环，走别的方向
        continue;
    }
    //如果(tx,ty)能走，那么它应该是之前没走过的点 且 不是障碍物的位置
    if(a[tx][ty]==0 && book[tx][ty]==0) {
        book[tx][ty] = 1;  //标记这个点已经走过
        dfs(tx,ty,step+1); // 代表走到(tx,ty)这个点，目前总共走了step+1步
        book[tx][ty]=0;
    }
}

 上面的代码有点难以理解，先说明a这个二维数组用来存储迷宫地图，其中值如果是1，代表(tx,ty)这个位置是障碍物，值如果是0，代表(tx,ty)是空地。走过的位置不能再走，因此使用book二维数组来标记某点在之前是否走过，值为0代表之前该点没有被走过，如果值为1，代表该点之前已经被走过了。

其中特别难理解的应该是为什么book[tx][ty]要重新标记为0呢？因为同一个点可能在多条路径上出现，如果在A路径出现了(tx,ty)这个点，那么我们会将book[tx][ty]赋值为1，而(tx,ty)这个点将来还有可能出现在别的到达终点的路径上，如果没有将book[tx][ty]用完之后赋值为0，那么将来别的到达终点的路径是无法走到(tx,ty)点上的，可能会导致答案错误。即本来经过(tx,ty)有路，结果因为book[tx][ty]为1，该点走不了，无法到达终点，但事实上我们可以到达终点的。

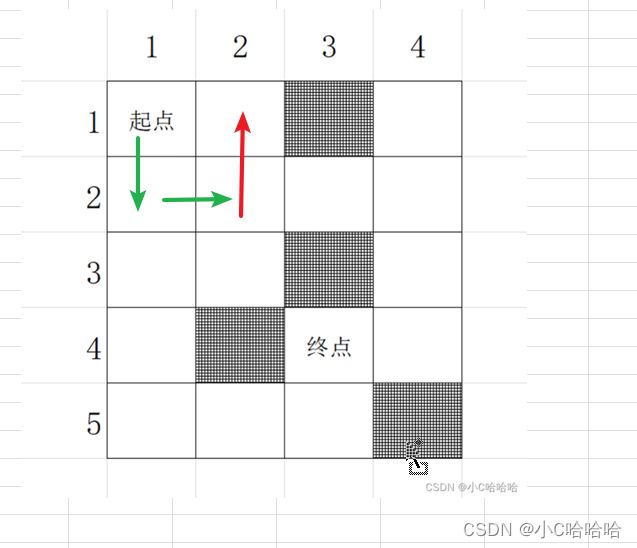
举个例子，如下： 在从(2,2)回退到(1,2)的时候，需要把book[2][2]赋值为0，代表该点此时已经不再属于某个路径中，标记为未访问的位置上，将来该点可以作为(1,1) -> (2,1) -> (2,2)该条路径上的坐标点。反正就是你用的时候别人不能用，你要不用了记得还回去，别人还要用呢！

 将上面的代码组装一下，我们可以得到迷宫问题的完整代码，如下：

#include
using namespace std;
int n,m,p,q,minn = 99999999;
int a[51][51]; //存储地图
int book[51][51]; //用来标记某点是否走过

void dfs(int x,int y,int step) {
	int next[4][2] = {
	{0,1},{1,0},{0,-1},{-1,0}};
	//判断是否到达终点位置
	if(x==p&&y==q) {
		//判断步数是否更短
		if(stepn||ty<1||ty>m) {
			continue;
		} 
		//判断该点是否为障碍物或者已经在路径中
		if(a[tx][ty]==0&&book[tx][ty]==0) {
			book[tx][ty]=1;
			dfs(tx,ty,step+1); //开始尝试下一个点
			book[tx][ty]=0; 
		} 
	}
}
int main() {
	int startx,starty;
	//n为行，m为列 
	cin >> n >> m;
	//读入n行m列的迷宫
	for(int i=1;i<=n;i++) {
		for(int j=1;j<=m;j++) {
			cin >> a[i][j];
		}
	}
	//读入起点坐标和终点坐标 
	cin >> startx >> starty >> p >> q;
	//从起点开始搜索
	book[startx][starty] = 1; //标记(startx,starty)已经在路径中，防止后面重复走
	//从startx,starty出发，目前到达该点需要0步 
	dfs(startx,starty,0); 
	cout << minn; //输出到达终点所需要的最短步数 
 	return 0;
}

 测试数据如下：

样例输入：

5 4
0 0 1 0
0 0 0 0
0 0 1 0
0 1 0 0
0 0 0 1
1 1 4 3

样例输出：
7