堆的相关操作（创建堆、插入、删除、堆排序、top-k问题）

一、什么是堆

堆得满足两个特性：1、首先得是一个完全二叉树

                                 2、每个节点比其孩子节点都大（小），则其是大（小）堆。

堆是将其元素存储在一维数组中的。

二、堆的创建

1、首先了解堆向下调整算法：

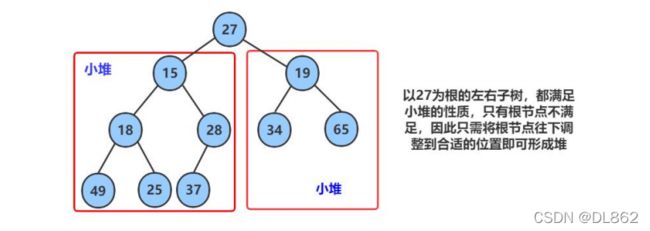
向下调整算法有一个前提：左右子树必须得是一个堆。如图所示，只有根节点不满足堆的特性。

 现在就来向下调整根节点，使其整体成为一个小堆。具体做法是让父节点和它较小的子节点交换（前提是左右节点都存在），然后再让父节点等于子节点；重复此操作，直到左儿子不存在。这样就把它调整成了一个小堆。这个算法的时间复杂度尾O（logN）。

代码：

//向下调整，前提是左子树和右子树都已经是小(大)堆
void AdjustDown(Heap* hp, int parent) {
	int child = parent * 2 + 1;
	while (child < hp->size) {
		//如果右儿子小于左儿子，child加一
		//为了能更灵活的创建大堆和小堆，这里用函数指针来代替比较关系
		if (child + 1 < hp->size && hp->com(hp->array[child + 1],hp->array[child])) {
			child++;
		}
		if (hp->com(hp->array[child],hp->array[parent])) {
			swap(&hp->array[parent], &hp->array[child]);
		}else {
			return;
		}
		parent = child;
		child = parent * 2 + 1;
	}
}

2、创建堆：

 如图，把这个完全二叉树（可以看作是一个一维数组）构建成一个小堆。具体做法为从倒数第一个非叶子节点开始，也就是28这个节点开始使用向下调整算法，依次调整25、19、18、15.这样就构建了一个小堆。

代码实现：

// 堆的构建
void myHeapCreate(Heap* hp, DataType a[], int n,Com com) {
	hp->array = (DataType*)malloc(sizeof(DataType)*n);
	if (hp->array == NULL) {
		assert(0);
		return;
	}
	memcpy(hp->array, a, n * sizeof(DataType));
	hp->capacity = n;
	hp->size = n;
	hp->com = com;
	//从倒数第一个节点开始，向下调整
	for (int root = (n - 2) / 2; root >= 0; root--) {
		AdjustDown(hp,root);
	}
}

3、时间复杂度：

构建堆的时间复杂度为O（N），证明如下： 

 

 三、堆的删除

堆删除操作删除的是根节点，具体做法为：

 首先把堆顶元素与最后一个元素交换，然后把堆中有效元素减一，最后将堆顶元素向下调整。

代码：

// 堆的删除
//删除的是堆顶元素
void HeapPop(Heap* hp) {
	if (HeapEmpty(hp)) {
		assert(0);
		return;
	}
	//将堆顶元素与最后一个元素交换
	swap(&hp->array[0], &hp->array[hp->size - 1]);
	//将有效元素个数减少一个
	hp->size--;
	//堆顶元素向下排序
	AdjustDown(hp, 0);
}

四、堆的插入

 

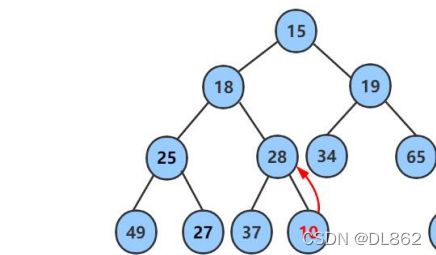
 如图所示，在堆尾插入10。我们只需要对10使用向上调整（和向下调整相似）。

代码

//向上调整
void AdjustUp(Heap* hp) {
	int child = hp->size - 1;
	while (child != 0) {
		int parent = (child - 1) / 2;
		if (hp->com(hp->array[child],hp->array[parent])) {
			swap(&hp->array[child], &hp->array[parent]);
		}else {
			return;
		}
		child = parent;
	}
}

// 堆的插入
//先检测空间，再在堆尾插入元素，最后再向上调整
void HeapPush(Heap* hp, DataType x) {
	CheakCapacity(hp);
	hp->array[hp->size] = x;
	hp->size++;
	AdjustUp(hp);
}

五、堆排序

堆排序的步骤：

1、建堆：排升序---------->大堆

                 排降序---------->小堆

2、利用堆删除思想进行排序

 如图所示已经构建了一个大堆，现在排升序。具体方法是，将堆顶元素和堆尾元素交换，这样就找到了最大值（这是大堆，堆顶元素是最大的），再把堆里的元素减一个，然后对堆顶元素进行向下调整；重复此操作。

代码实现：

//堆排序,升序


#if 1
//堆排序向下调整，parent为要调整的节点，size为堆的大小
void SortAdjustDown(int array[], int parent, int size) {
	int child = parent * 2 + 1;
	while (child < size) {
		if (child + 1 < size && array[child] < array[child + 1]) {
			child++;
		}
		if (array[parent] < array[child]) {
			/*int temp = array[parent];
			array[parent] = array[child];
			array[child] = temp;*/
			swap(&array[parent], &array[child]);
		}
		else {
			return;
		}
		parent = child;
		child = parent * 2 - 1;
	}
}

void HeapSort(int array[],int size) {
	int root = (size - 2) / 2;
	//先创建一个大堆
	for (root; root >= 0; root--) {
		SortAdjustDown(array, root, size);
	}
	int end = size - 1;
	//把堆尾元素和堆顶元素交换，让堆的元素个数减一，然后
	//再把堆顶元素向下调整，这样就把最大的节点调整到了堆尾,重复此操作
	while (end > 0) {
		/*int temp = array[0];
		array[0] = array[end];
		array[end] = temp;*/
		swap(&array[0], &array[end]);
		SortAdjustDown(array, 0, end);
		end--;
	}
}

六、top-k问题：即求一组数据最大或最小的几个数，如世界五百强。

1、利用前k个元素构建一个堆

前k个最大的元素---------小堆（因为要拿其他元素和堆中最小的（堆顶）元素比较）

前k个最小的元素-----------大堆

2、拿堆顶元素和其他元素比较，如果不满足条件，就把堆顶元素替换掉，然后进行向下调整。