C语言数据结构初阶(10)----二叉树的实现

· CSDN的uu们，大家好。这里是C语言数据结构的第十讲。
· 目标：前路坎坷，披荆斩棘，扶摇直上。
· 博客主页： @姬如祎
· 收录专栏： 数据结构与算法

 

 

目录

1. 函数接口一览

2. 函数接口的实现

2.1 BTNode* BuyNode(BTDataType x) 的实现

2.2 BTNode* CreateTree() 的实现

 2.3 void TreeDestroy(BTNode* root) 的实现

2.4 void PrevOrder(BTNode* root) 的实现

2.5 void InOrder(BTNode* root) 的实现

2.6 void PostOrder(BTNode* root) 的实现

2.7 void LevelOrder(BTNode* root) 的实现

2.7 int TreeSize(BTNode* root) 的实现

2.8 int TreeHeight(BTNode* root) 的实现

2.9 int TreeLevel(BTNode* root, int k) 的实现

 2.10 BTNode* TreeFind(BTNode* root, BTDataType x) 的实现

说明：因为是数据结构初阶，所以二叉树的创建方式我们选择直接开辟节点，然后手动链接。二叉树真正的创建方式在高阶的数据结构再来实现。因为我们实现的二叉树只是普通的二叉树，增删改查没有什么意义。像哪些特殊的二叉树，红黑树等的增删改查才有意义。这里这是通过常见接口的讲解来理解二叉树递归的性质。

1. 函数接口一览

typedef int BTDataType;
typedef struct BinaryTree
{
	BTDataType data;
	struct BinaryTree* left;
	struct BinaryTree* right;
} BTNode;

//开辟一个节点
BTNode* BuyNode(BTDataType x);

//二叉树的手动创建
BTNode* CreateTree();

//二叉树的销毁
void TreeDestroy(BTNode* root);

//二叉树的前序遍历
void PrevOrder(BTNode* root);

//二叉树的中序遍历
void InOrder(BTNode* root);

//二叉树的后序遍历
void PostOrder(BTNode* root);

//二叉树的层序遍历
void LevelOrder(BTNode* root);

//二叉树的节点个数
int TreeSize(BTNode* root);

//二叉树的深度
int TreeHeight(BTNode* root);

//二叉树第K层的节点个数
int TreeLevel(BTNode* root, int k);

//二叉树查找节点值为X的节点
BTNode* TreeFind(BTNode* root, BTDataType x);

2. 函数接口的实现

2.1 BTNode* BuyNode(BTDataType x) 的实现

这个函数和链表中申请节点的作用相同，均是为了方便构建数据结构。在向堆区申请空间后需要将该节点的左右孩子的指针初始化为NULL。

//开辟一个节点
BTNode* BuyNode(BTDataType x)
{
	//堆区开辟节点
	BTNode* newNode = (BTNode*)malloc(sizeof(BTNode));
	if (newNode == NULL)
	{
		perror("BuyNode::malloc");
		exit(-1);
	}
	else
	{
		//节点初始化
		newNode->data = x;
		newNode->left = NULL;
		newNode->right = NULL;
		return newNode;
	}
}

2.2 BTNode* CreateTree() 的实现

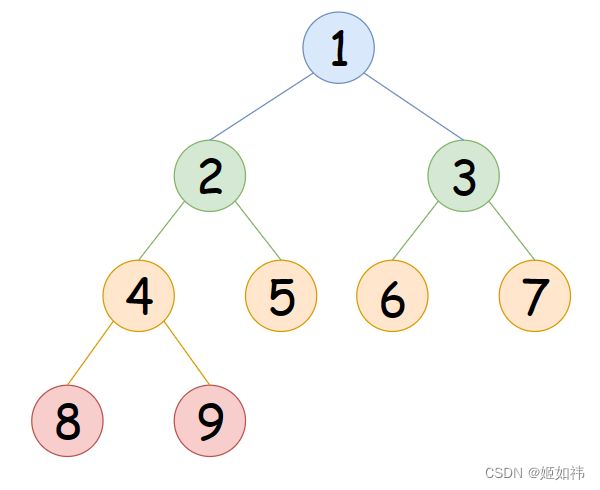
文章开头我们就说明了，我们学的是最普通的二叉树，因此为了 方便起见，我们选择手动进行二叉树的构建。方法很简单，你只需要开辟你所需要构建的树的节点个数，然后将指针链接起来即可。这里我们构建一颗如下图所示的完全二叉树。

//二叉树的手动创建
BTNode* CreateTree()
{
	BTNode* node1 = BuyNode(1);
	BTNode* node2 = BuyNode(2);
	BTNode* node3 = BuyNode(3);
	BTNode* node4 = BuyNode(4);
	BTNode* node5 = BuyNode(5);
	BTNode* node6 = BuyNode(6);
	BTNode* node7 = BuyNode(7);
	BTNode* node8 = BuyNode(8);
	BTNode* node9 = BuyNode(9);

	node1->left = node2;
	node1->right = node3;

	node2->left = node4;
	node2->right = node5;

	node3->left = node6;
	node3->right = node7;

	node4->left = node8;
	node4->right = node9;

	return node1;
}

 2.3 void TreeDestroy(BTNode* root) 的实现

二叉树的初阶内容不涉及数据的增删改查，我们学习的主要内容就是理解二叉树的递归特性。为将来学习特殊的二叉树打好基础。因此下面开始的函数均选择使用递归来实现。

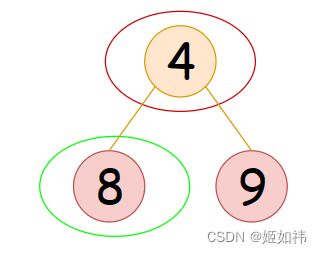
这个函数的实现比较简单，但是释放节点的顺序还是有讲究的，如下图，我们要对这三个节点进行释放，我们有三个选择：先释放4；先释放8；先释放9。显然我们不会选择先释放4，因为如果你想要先释放4，那么你还需要用变量先保存4的左右孩子，这样就显得比较麻烦啦。至于是先释放8.还是先释放9，就没有优劣之差啦。

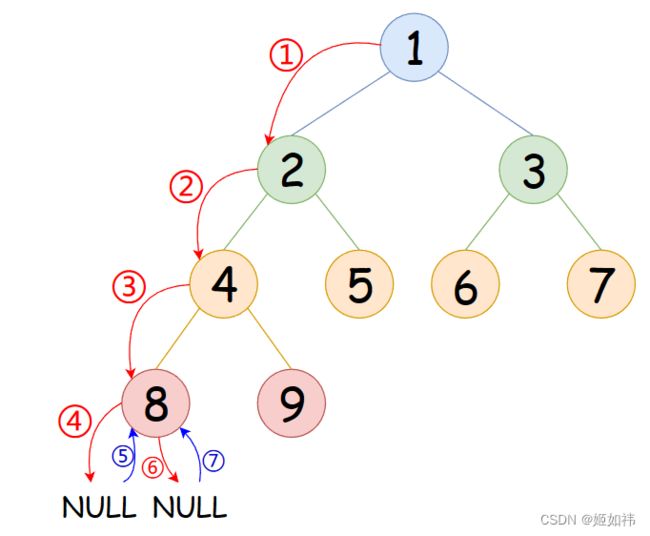
 在释放树的节点时，显然只能从叶子节点开始释放，这恰恰符合了递归递去归来的特性，因此我们选择使用递归来实现。通过递归，先到达叶子节点，我们不妨先释放左孩子，再释放右孩子，如果左右孩子不为空，我们就释放他们，然后再释放左右孩子的双亲节点，释放完成后逐步向上返回，直到将根结点释放。下图展示了8这个节点的销毁过程，请结合代码进行理解。

//二叉树的销毁
void TreeDestroy(BTNode* root)
{
	if (root == NULL)
		return;
	TreeDestroy(root->left);
	TreeDestroy(root->right);

	free(root);
	root = NULL;
}

2.4 void PrevOrder(BTNode* root) 的实现

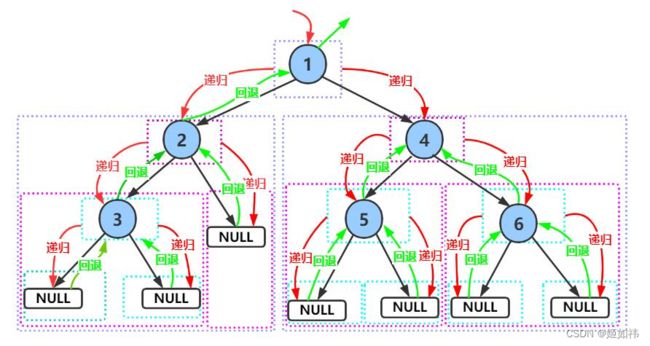
 前序遍历，就是在遍历二叉树时先访问根结点，在访问左子树，最后访问右子树。二叉树的递归逻辑都是相似的，可以结合下面的这张图来理解前序遍历。

 在进行前序遍历的时候，他的本质是会去访问叶子节点左右孩子的那两个NULL指针的，因此在访问到NULL时，我们可以将NULL打印出来，这样能更加深刻的理解前序遍历的本质。

//二叉树的前序遍历
void PrevOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	printf("%d ", root->data);
	PrevOrder(root->left);
	PrevOrder(root->right);

}

2.5 void InOrder(BTNode* root) 的实现

中序遍历就是在遍历二叉树的时候先访问左子树，再访问根结点，最后访问右子树。思路就是二叉树的递归思路，代码只需要将前序遍历代码的顺序交换一下即可。

void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	InOrder(root->left);
	printf("%d ", root->data);
	InOrder(root->right);

}

2.6 void PostOrder(BTNode* root) 的实现

后续遍历就是指在遍历二叉树时先访问左子树，再访问右子树，最后访问根结点。

void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d ", root->data);

}

2.7 void LevelOrder(BTNode* root) 的实现

层序遍历就是将一棵树按照每一层每一层的方式进行遍历，下图中的二叉树的层序遍历结果就是：1 2 3 4 5 6 7 8 9

这该怎么做呢？其实很简单，我们只需要维护一个队列， 一开始呢，先将根结点入队列。然后进入一个循环，循环继续的条件就是队列不为空，然后逐步取出队头的元素，如果队头元素的左右孩子有不为空的，就将其入队列，依次类推，节点从队列中出来的顺序就是层序遍历的结果。

至于队列的选择，我们选择使用数组模拟实现队列，因为C语言嘛，不像其他语言那么方便。

关于数组模拟实现队列，请参考：数据模拟实现队列

2.7 int TreeSize(BTNode* root) 的实现

你可能会想，我们维护一个变量Size，然后将二叉树遍历一遍，每遍历到一个节点就将Size++，这样就能求出二叉树的节点个数了。这没问题，很好，只不过这种方法有一点值得注意，如果你不使用全局或者静态变量，而是将Size作为参数传递给TreeSize函数，那么，一定记得传指针哦！具体原因想必大家都懂啦！俺们都是C语言学完的人了！但是这里不推荐使用全局和静态的变量。如果你要对多棵树调用该方法，那么你还得重新初始化这个全局变量，比较麻烦。

这里我们就不对上面的这种方法做实现啦！这里还有一种方法：整个二叉树节点的个数就等于左子树节点的个数 + 右子树节点的个数 + 1 (这个1就是根节点啦)。这便是分治思想。将大的问题拆解成小的问题(说实话还有一点动态规划的味道)。

int TreeSize(BTNode* root)
{
	if (root == NULL)
		return 0;
	return TreeSize(root->left) + TreeSize(root->right) + 1;
}

2.8 int TreeHeight(BTNode* root) 的实现

我们理解了求解TreeSize的思路，TreeHeight就是信手拈来的事情。同样地，我们利用分治的思想：树的深度 = 左右子树中深度较大的那一个 + 1，是不是很简单嘞。

int TreeHeight(BTNode* root)
{
	if (root == NULL)
		return 0;
	int left = TreeHeight(root->left);
	int right = TreeHeight(root->right);
	return left > right ? left + 1 : right + 1;
}

2.9 int TreeLevel(BTNode* root, int k) 的实现

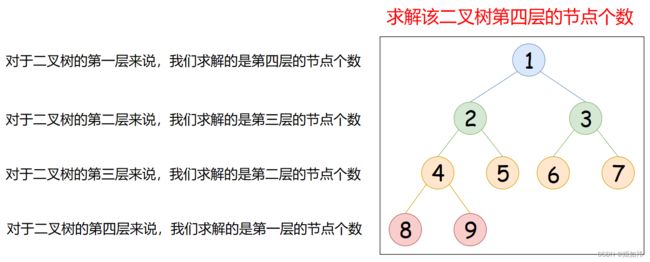
求解二叉树第K层的节点个数，怎么用分治的思想解决呢？上图解

 这下是不是有思路了呢？当我们递归到所求节点总数的那一层时，对于K = 1，而这个时候呢，我们就不要向下递归啦！这层有节点的话，递归到此层的每一个节点返回1就行啦！

int TreeLevel(BTNode* root, int k)
{
	if (root == NULL)
	{
		return 0;
	}
	if (k == 1)
	{
		return 1;
	}
	return TreeLevel(root->left, k - 1) + TreeLevel(root->right, k - 1);
}

 2.10 BTNode* TreeFind(BTNode* root, BTDataType x) 的实现

咦，不是说普通的二叉树不学增删改查吗！哈哈，勉强看一个吧，这里有一个地方值得注意，TreeFind函数的返回值不是bool值而是查找到的节点，如果有修改的需要，我们就能够在查找的同时对节点的值进行修改啦！是不是很方便。

怎么实现这个函数呢？其实很简单，我们先对每一层递归的根结点进行判断，如果这个时候根结点的data就等于x那么直接返回结果就行。如果根结点的data值不等于x呢？

我们就在根结点的左子树中去找，也就是往左子树递归、如果在左子树找的结果不为空，说明在左子树中找到了data值为x的节点，返回该节点即可！

如果左子树没找到，就在右子树中去找，也就是往右子树去递归。如果在右子树找的结果不为空，说明在右子树中找到了data值为x的节点，返回该节点即可！如果在右子树中没有找到嘞，说明左右子树都没找到，返回NULL即可。

BTNode* TreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
	{
		return NULL;
	}
	if (root->data == x)
		return root;
	BTNode* left = TreeFind(root->left, x);
	if (left)
		return left;

	BTNode* right = TreeFind(root->right, x);
	if (right)
		return right;
	
	return NULL;
}