[论文精读]How Powerful are Graph Neural Networks?
论文原文:[1810.00826] How Powerful are Graph Neural Networks? (arxiv.org)
英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用!
1. 省流版
1.1. 心得
①Emm, 数学上的解释性确实很强了
②他一直在...在说引理
1.2. 论文框架图
2. 论文逐段精读
2.1. Abstract
①Even though the occurrence of Graph Neural Networks (GNNs) changes graph representation learning to a large extent, it and its variants are all limited in representation abilities.
2.2. Introduction
①Briefly introduce how GNN works (combining node information from k-hop neighbors and then pooling)
②The authors hold the view that ⭐ other graph models mostly based on plenty experimental trial-and-errors rather than theoretical understanding
③They combine GNNs and the Weisfeiler-Lehman (WL) graph isomorphism test to build a new framework, which relys on multisets
④GIN is excellent in distinguish, capturing and representaion
heuristics n.[U] (formal) 探索法;启发式
heuristic adj.(教学或教育)启发式的
2.3. Preliminaries
(1)Their definition
①They define two tasks: node classicifation with node label ![]() and graph classification with graph label
and graph classification with graph label ![]()
(2)Other models
①The authors display the function of GNN in the ![]() -th layer:
-th layer:
where only ![]() is initialized to
is initialized to ![]() (其余细节就不多说了,在GNN的笔记里都有)
(其余细节就不多说了,在GNN的笔记里都有)
②Pooling layer of GraphSAGE, the AGGREGATE function is:
where MAX is element-wise max-pooling operator;
![]() is learnable weight matrix;
is learnable weight matrix;
and followed by concatenated COMBINE and linear mapping ![]()
③AGGREGATE and COMBINE areintegrated in GCN:
④Lastly follows a READOUT layer to get final prediction answer:
![]()
where the READOUT function can be different forms
(3)Weisfeiler-Lehman (WL) test
①WL firstly aggregates nodes and their neighborhoods and then hashs the labels (??hash?这好吗)
②Based on WL, WL subtree kernel was proposed to evaluate the similarity between graphs
③A subtree of height ![]() 's root node is the node at
's root node is the node at ![]() -th iteration
-th iteration
permutation n.置换;排列(方式);组合(方式)
2.4. Theoretical framework: overview
①The framework overview
②Multiset: is a 2-tuple ![]() , where "where
, where "where ![]() is the underlying set of
is the underlying set of ![]() that is formed from its distinct elements, and
that is formed from its distinct elements, and ![]() gives the multiplicity of the elements" (我没有太懂这句话欸)
gives the multiplicity of the elements" (我没有太懂这句话欸)
③They are not allowed that GNN map different neighbors to the same representation. Thus, the aggregation must be injective (我也不造为啥)
2.5. Building powerful graph neural networks
①They define Lemma 2, namely WL graph isomorphism test is able to correctly distinguish non-isomorphic graphs
②Theorem 3 完全没看懂
③Lemma 4: If input feature space is countable, then the space of node hidden features ![]() is also countable
is also countable
2.5.1. Graph isomorphism network (GIN)
①Lemma 5: there is ![]() , which makes
, which makes ![]() unique in
unique in ![]() . Also there is
. Also there is ![]()
②Corollary 6: there is unique ![]() and
and ![]() .
.
③Finally, the update function of GIN can be:
2.5.2. Graph-level readout of GIN
①Sum, mean and max aggregators:
②The fail examples when the different ![]() and
and ![]() map the same embedding:
map the same embedding:
where (a) represents all the nodes are the same, only sum can distinguish them;
blue in (b) represents the max, thus max fails to distinguish as well;
same in (c). (盲猜这里其实蓝色v自己是一个节点,但是没有考虑自己的特征,而是纯看1-hop neighborhoods)
③They change the READOUT layer to:
2.6. Less powerful but still interesting GNNs
They designed ablation studies
2.6.1. 1-layer perceptrons are not sufficient
①1-layer perceptrons are akin to linear mapping, which is far insufficient for distinguishing
②Lemma 7: notwithstanding multiset ![]() is different from
is different from ![]() , they might get the same results:
, they might get the same results: ![]()
2.6.2. Structures that confuse mean and max-pooling
这一节的内容在2.5.2.②的图下已经解释过了
2.6.3. Mean learns distributions
①Collary 8: there is a function ![]() . If and only if multisets
. If and only if multisets ![]() and
and ![]() are the same distribution,
are the same distribution, ![]()
②When statistical and distributional information in graph cover more important part, mean aggregator performs better. But when structure is valued more, mean aggregator may do worse.
③Sum and mean aggregator may be similar when node features are multifarious and hardly repeat
2.6.4. Max-pooling learns sets with distinct elements
①Max aggregator focus on learning the structure of graph (原文用的"skeleton"而不是"structure"), and it has a certain ability to resist noise and outliers
②For max function ![]() , if and only if
, if and only if ![]() and
and ![]() have the same underlying set,
have the same underlying set, ![]()
2.6.5. Remarks on other aggregators
①They do not cover the analysis of weighted average via attention or LSTM pooling
2.7. Other related work
①Traditional GNN does not provide enough math explanation
②Exceptionally, RKHS of graph kernels (?) is able to approximate measurable functions in probability
③Also, they can hardly generalize to multple architectures
2.8. Experiments
(1)Datasets
①Dataset: 9 graph classification benchmarks: 4 bioinformatics datasets (MUTAG, PTC, NCI1, PROTEINS) and 5 social network datasets (COLLAB, IMDB-BINARY, IMDB-MULTI, REDDITBINARY and REDDIT-MULTI5K)
②Social networks are lack of node features, then they set node vectors as the same in REDDIT and use one hot encoding for others
(2)Mondels and configurations
①They set two variants, the one is GIN-ε, which adopts gradient descent, the other one is GIN-0, which is a little bit simpler.
②Performances of different variants on different datasets
③Validation: 10-fold LIB-SVM
④Layers: 5, includes input layer, and each MLP takes two layers
⑤Normalization: batch normalization for all hiden layers
⑥Optimizer: Adam
⑦Learning rate: 0.01 at first and substract 0.5/50 epochs
⑧Number of hidden units, hyper parameter: 16 or 32
⑨Batch size: 32 or 128
⑩Drop out ratio: 0 or 0.5
⑪Epoch: the best one in 10-fold
(3)Baselines
①WL subtree kernel
②Diffusionconvolutional neural networks (DCNN), PATCHY-SAN (Niepert) and Deep Graph CNN (DGCNN)
③Anonymous Walk Embeddings (AWL)
2.8.1. Results
(1)Training set performance
①Training set accuracy figure was showed above
②WL always performs better than GNN due to its strong classifying ability. However, WL can not present the node features combination, which may limit in the future
(2)Test set performance
①Test set classification accuracies
②GIN-0 obviously outperforms others
2.9. Conclusion
They give theoretical foundations of graph structure and discuss the performances of variants of GNN. Then, they designed a strong GNN, named GIN to achieve more accurate classification. Furthermore, they think researching the generalization for GNNs is also promising.
3. Reference List
Xu, K. et al. (2019) 'How Powerful are Graph Neural Networks?', ICLR 2019. doi: https://doi.org/10.48550/arXiv.1810.00826
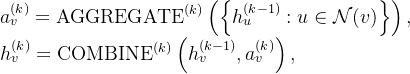
![[论文精读]How Powerful are Graph Neural Networks?_第1张图片](http://img.e-com-net.com/image/info8/6fbacac845174db583b922c36c12c61c.jpg)
![[论文精读]How Powerful are Graph Neural Networks?_第2张图片](http://img.e-com-net.com/image/info8/d2565c4eef824095aac98f0fe969d4ec.jpg)
![[论文精读]How Powerful are Graph Neural Networks?_第3张图片](http://img.e-com-net.com/image/info8/7055132d79e049a28e0c7511adeb3e73.jpg)
![[论文精读]How Powerful are Graph Neural Networks?_第4张图片](http://img.e-com-net.com/image/info8/41ab112cde144f91be247d7db6b3c3e1.jpg)
![[论文精读]How Powerful are Graph Neural Networks?_第5张图片](http://img.e-com-net.com/image/info8/979cf4af604d410ea71367b6fe98d3ab.jpg)