二叉树的递归和非递归遍历

二叉树的遍历(Traversal)有多种方式，包括：

• 先序遍历(Preorder)

• 中序遍历(Inorder)

• 后序遍历(Postorder)

• 层次遍历

而他们的实现方式也有多种，首先我们看看是如何遍历一颗二叉树的（在不借助计算机编程的情况下）。

我们可以将二叉树的树形结构画出，用笔绕着二叉树的各个节点走一圈，相当于用线条把二叉树的树形结构给围起来，观察线条与二叉树的节点的位置关系。

我们知道二叉树的遍历结果都是一个由他的节点元素组成的一个序列，因此所有的节点在遍历的过程中都会被访问到，但是访问的先后顺序是有区别的。模拟用笔绕圈的过程，如果笔尖划出的线条经过了一个节点的左边，这个节点的元素就应该添加到先序遍历的序列中，如果经过了一个节点的下边（这种情况只会出现在这个节点没有儿子需要往回走），就将这个元素添加到中序遍历的序列中，如果经过了一个节点的右边（说明已经在往回走了），就将这个元素添加到后序遍历的序列中。当走完一圈，我们就得到了二叉树三种遍历的结果。

关于使用计算机编程来求出二叉树遍历序列的方式也是有很多种的，为了表示方便，建议读者去力扣搜搜二叉树这本教程来阅读，并完成里面的配套练习，我这里所用的题目以及下面所给出的参考代码都与力扣上的题目配套（也在它的二叉树教程中）

力扣《二叉树教程》链接

递归实现

使用递归实现这三种遍历方式是非常简单的，我们只需依次递归调用当前节点的左子树和右子树（如存在），只需改变输出元素这个语句的位置即可。但访问顺序都是一样，我们始终先走左子树，没有后走右子树，最后返回。有意思的是，由于使用递归的方式递归函数的结构是完全一致的，所以这里我分别用C、C++和Python来实现。

---

先序遍历

144. 二叉树的前序遍历

给你二叉树的根节点 root ，返回它节点值的 前序 遍历。

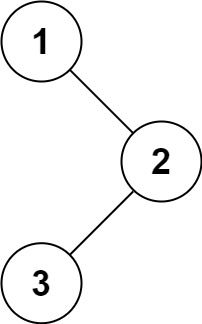
输入：root = [1,null,2,3]
输出：[1,2,3]
提示：
树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100

---

如有左子树，就递归访问左子树，如有右子树，就递归访问右子树（这个过程在递归的三种遍历过程都是一样的，即使你用我上面的笔画法，也是按照这个顺序）

输出遍历序列的时机：遇到一个节点就可以将其输出（它是最先访问到的），然后再执行递归函数

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */


/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
void preorder(struct TreeNode *now,int *ans,int *cnt)//我们的递归函数
{
    //printf("%d ",now->val);
    ans[(*cnt)++]=now->val; //数组大小用指针传递
    if (now->left)
    preorder(now->left,ans,cnt);
    if (now->right)
    preorder(now->right,ans,cnt);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize)
{
    int *ans=(int *)malloc(sizeof(int)*101);
    returnSize=0; //力扣中C语言返回数组要定义长度
    if (root)
    	preorder(root,ans,returnSize); //调用递归函数
    return ans;
}

---

中序遍历

94. 二叉树的中序遍历

给定一个二叉树的根节点 root ，返回 它的 中序 遍历 。

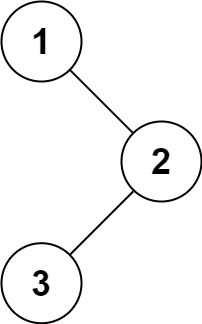
输入：root = [1,null,2,3]
输出：[1,3,2]

---

输出遍历序列的时机：如果这个节点有左子树，要等到他递归调用完左子树的函数（一路这样下去）并返回到这个节点时输出；如果没有左子树，就直接输出；然后才去递归调用右子树。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void inOrder(TreeNode *now,vector<int> &ans) //递归函数使用引用方式传参
    {
        if (now->left)
            inOrder(now->left,ans);
        ans.emplace_back(now->val);
        if (now->right)
            inOrder(now->right,ans);
    }
    vector<int> inorderTraversal(TreeNode* root) 
    {
        vector<int> ans;
        if (root)
            inOrder(root,ans);
        return ans;
    }
};

---

后序遍历

145. 二叉树的后序遍历

给你一棵二叉树的根节点 root ，返回其节点值的 后序遍历 。

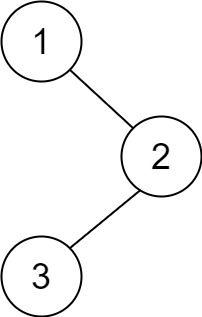
输入：root = [1,null,2,3]
输出：[3,2,1]

---

输出遍历序列的时机：只有当该节点的左子树和右子树都递归访问完（若有），后才将该节点的元素放入输出序列

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:

    def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]: 
        def postorder(now,ans): #Python都是地址传递
            if now.left:
                postorder(now.left,ans)
            if now.right:
                postorder(now.right,ans)
            ans.append(now.val)
        ans=[] #存放后序遍历的List
        if root:
            postorder(root,ans)
        return ans

---

非递归做法

进阶：递归算法很简单，你可以通过迭代算法完成吗？

首先我们要思考我们解决这个问题的本质到底是什么，递归函数的作用是什么？
其实递归就是调用系统栈的过程，同样的，不借助递归，我们通过手写栈也能完成这个过程。

先序遍历

我们首先搞清楚递归函数中隐藏的栈的调用过程才能自己实现一个栈，我们需要找出二叉树每个节点入栈和出栈的时机以及输出序列的操作发生在什么时候。

观察递归函数发现，我们向系统栈中添加一个元素总是先添加当前元素的左子树，若左子树不存在，就添加栈顶元素的右子树，然后退栈。

由此得到一个策略：
-先将根节点入栈
-每遇到一个节点就将节点的值添加到先序遍历序列中去
-如有左节点，左节点入栈，直到当前节点没有左节点
-如果当前节点有右节点，右节点入栈；若无，退栈
-重复前两步操作，直到栈为空

对每个节点，如果有左节点，while循环并让当前节点变为当前元素的左孩子节点，同时将其入栈，直到当前节点不存在左节点，然后这时候我们要原路返回，并注意栈内元素是否有右孩子节点，如果有我们就要（跳出退栈的循环，在程序中，逻辑上不是）将它入栈，找它的左节点，重复…

在实际编写程序的过程中，我们要注意根节点为空的处理以及退栈时栈的容量要大于1的问题
同时。并且很容易出现死循环的问题，通常是因为前面的节点在栈中没有弹出，当重新进入外层循环时候重复进行操作，所以我们要适时将节点弹出避免重复访问其某课子树，如下面我的代码访问右子树时就已经将当前节点弹出，可以将该节点先保存起来访问。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) 
    {
        stack<TreeNode*> stk;
        stk.push(root);
        TreeNode *now;
        vector<int> ans;
        if (!root)
            return ans;
        ans.push_back(root->val);
        while (!stk.empty())
        {
            now=stk.top();
            while (now->left)
            {
                now=now->left;
                ans.push_back(now->val);
                stk.push(now);
            }
            //cout<val<
            while (stk.size())
            {
                now=stk.top();
                if (now->right)
                break;
                //cout<val<<" "<
                stk.pop();
            }
            if (stk.size())
            {
                now=stk.top();
                if (now->right)
                {
                    stk.pop();
                    now=now->right;
                    ans.push_back(now->val);
                    stk.push(now);
                }
            }
        }
        return ans;
    }
};

中序遍历

由于先访问了该节点的左子树才输出该节点到中序遍历序列中，然后访问右子树。所以程序的框架可以沿用先序遍历上面的写法，当退栈的时候将节点加入序列。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) 
    {
        stack<TreeNode*> stk;
        vector<int> ans;
        if (root)
            stk.push(root);
        TreeNode* now;
        while (stk.size())
        {
            now=stk.top();
            while (now->left)
            {
                now=now->left;
                stk.push(now);
            }
            while (stk.size())
            {
                now=stk.top();
                ans.emplace_back(now->val);
                if (now->right)
                    break;
                stk.pop();
            }
            if (now->right)
            {
                stk.pop();
                now=now->right;
                stk.push(now);
            }
        }
        return ans;
    }
};

后序遍历

不幸的是，我发现上面的用于前序和中序遍历的非递归代码无法解决后序遍历的非递归问题，因为正如我在前序遍历最后一段所说，为了避免重复访问某一课子树，要将元素从栈中适时弹出，但后序遍历中的元素是访问过左子树和右子树返回后的时机所添加的，但之前在左子树递归完成返回（前序）或者访问右子树之前（中序），上述代码已经将当前节点弹出，我们无从访问！反过来看递归，在递归函数的返回过程中又重新进入了之前的函数空间，而函数的参数里还存储着当前节点的信息，并继续返回过程。我们执行完递归语句，回到的是这一函数的这一条语句的下面，但这在迭代过程中是难以实现的。

还有什么方法吗？
观察后序遍历序列的特点得知其先出现右子树的元素，然后是左子树的元素，最后是根节点，所以我们先让左子树进栈，再让右子树进栈，在下一层循环的时候我们出栈就访问的是右子树的元素，并在栈顶元素出栈之前将其添加进序列中去，这一过程如果应用到前序遍历上是完全相反的，相当于翻转了这颗二叉树，所以最后要将序列反转。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        stack<TreeNode*> stk;
        vector<int> ans;
        if (root)
            stk.push(root);
        while (stk.size())
        {
            TreeNode* now=stk.top();
            ans.emplace_back(now->val);
            stk.pop();
            if (now->left)
                stk.push(now->left);
            if (now->right)
                stk.push(now->right);
        }
        reverse(ans.begin(),ans.end());
        return ans;
    }
};

将这个思路应用到前序遍历中去，只需将入栈的顺序对调。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) 
    {
        stack<TreeNode*> stk;
        vector<int> ans;
        if (root)
            stk.push(root);
        while (stk.size())
        {
            TreeNode* now=stk.top();
            stk.pop();
            ans.emplace_back(now->val);
            if (now->right)
            stk.push(now->right);
            if (now->left)
            stk.push(now->left);
        }
        return ans;
    }
};

个人觉得这种方法类似于BFS的实现过程。只是这里运用的是栈。

层次遍历

最后我们来讲一下二叉树的层次遍历，这正是通过BFS来实现的。

102. 二叉树的层序遍历

首先将头结点入队，进入一个队列的循环，当队列非空的时候，取出队头元素，并将其弹出队列，依次将队头元素的左孩子节点和右孩子节点入队，这样就能保证在输出遍历序列时候是按照二叉树从左向右，从上到下的顺序的。但题目要求输出成二维数组的形式，每一层的结果都用一个数组来存储，所以我们还要维护节点的层数，所以将节点和层数捆绑成一个pair一起存入队列。具体实现如下。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) 
    {
        if (!root)
            return {};
        queue<pair<TreeNode*,int>> q;
        q.push({root,0});
        vector<vector<int>> ans;
        vector<int> res;
        while (!q.empty())
        {
            auto it=q.front();
            q.pop();
            TreeNode* now=it.first;
            int lv=it.second;
            if (lv<=ans.size())
            res.emplace_back(now->val);
            else
            {
                ans.emplace_back(res);
                while (res.size()) //将res数组清空
                res.pop_back();
                res.emplace_back(now->val); //别忘了添加res的头元素
            }
            if (now->left)
                q.push({now->left,lv+1});
            if (now->right)
                q.push({now->right,lv+1});
        }
        ans.emplace_back(res);
        return ans;
    }
};