leetcode：210. 课程表 II
题目来源
- leetcode
题目描述
题目解析
- 拓扑排序是专门应用于有向图的算法。 只有有向无环图才有拓扑序
- 拓扑排序就是带有贪心算法的BFS，贪的点是：当前让入度为 0 的那些结点入队；
- 拓扑排序的作用：
- 检查有向图是否存在环
- 得到拓扑序。有时候拓扑序并不是唯一的，所以面试的时候要问下面试官，是要求解任意解，还是列出所有解。
拓扑排序就是带有贪心算法的BFS，贪的点是：当前让入度为 0 的那些结点入队。关键在于，每次只选那些你能上的课，即每次只能选入度为0的课，因为它不依赖别的课。举个例子：
- 假设选了 0，导致 依赖 0 的课的入度减小，课 3 的入度由 2 变 1
- 接着选 1，导致课 3 的入度变 0，课 4 的入度由 2 变 1
- 接着选 2，导致课 4 的入度变 0，当前 3 和 4 入度为 0
- 继续选 入度为 0 的课 …… 直到选不到 入度为 0 的课
即可以这么做？：
- 起初让入度为0的课入队
- 然后逐个出对，出队即选课，并减小相关课的入度
- 判定是否有课的入度新变为 0，安排入列、再出列……
- 直到没有 入度为 0 的课 可入列……
从上面我们可以看出：
- 我们关心每一节课的入度
- 我们关心课程之间的依赖关系
那么应该怎么实现呢？创建一个入度数组和邻接表
- 课号是0到n-1，作为索引，值为入度，遍历先决条件，求出每门课的初始入度
- 用哈希表记录依赖关系
- key：课程编号
- value：依赖它的后继课程
BFS思路：
- queue队列中始终是入度为0的课程在里面流动
- 选择一门课，就让它出队，同时查看哈希表，看它对应哪些后继课程
- 将这些后继课程的入度-1，如果有减到0的，就将它推入queue
- 当不再有新的入度为0的课程入列，此时queue为空，退出循环
class Solution {
public:
vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
vector<int> res;
int *inDegree = new int [numCourses]{0};
int size = prerequisites.size();
unordered_map<int, list<int>> map;
queue<int> Queue;
// 创建入度表和哈希表
for (int i = 0; i < size; ++i){
inDegree[prerequisites[i][0]]++;
map[prerequisites[i][1]].push_back(prerequisites[i][0]);
}
// 将index入队
for (int i = 0; i < numCourses; ++i){
if (inDegree[i] == 0){
Queue.push(i);
}
}
// 出队, 查哈希表, 将入队为零的入队
while (!Queue.empty()){
int cur = Queue.front();
res.push_back(cur);
Queue.pop();
if (map[cur].size() != 0){
for (auto num : map[cur]){
inDegree[num]--;
if (inDegree[num] == 0) Queue.push(num);
}
}
}
return res.size() == numCourses ? res : vector<int>();
}
};
只有有向无环图才有拓扑序
拓扑排序并不是一个纯粹的排序算法，它只是针对某一类图，找到一个可以执行的线性顺序。
针对哪类图呢？有向无环图。即使：
- 这个图的边必须是有方向的；
- 图内无环。
那么什么是方向呢？
= 比如微信好友就是有向的，你加了他好友他可能把你删了你却不知道。。。那这个朋友关系就是单向的。。
什么是环？
-
环是和方向有关的，从一个点出发能回到自己，这是环。
-
所以下图左边不是环，右边是。
-
那么如果一个图里有环，比如右图，想执行1就要先执行3，想执行3就要先执行2，想执行2就要先执行1，这成了个死循环，无法找到正确的打开方式，所以找不到它的一个拓扑序。
结论：
- 如果这个图不是 DAG，那么它是没有拓扑序的；
- 如果是 DAG，那么它至少有一个拓扑序；
- 反之，如果它存在一个拓扑序，那么这个图必定是 DGA。
怎样应用可以用拓扑排序
对于本题，拓扑排序的意思是：求解一种可行的顺序，能够让我把所有课都学了。
那应该怎么做呢？
（1）首先我们可以用图来描述它，图的两个要素是顶点和边，那么在这里：
- 顶点：每门课
- 边：起点的课程是终点的课程的先修课
假如有一个这样的图：
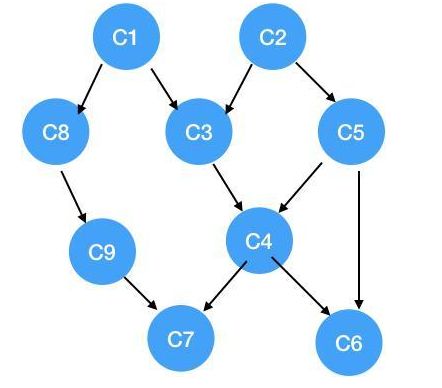
这种图叫AOV(Activity On Vertex) 网络，在这种图里：
- 顶点：表示活动；
- 边：表示活动间的先后关系
所以一个 AOV 网应该是一个 DAG，即有向无环图，否则某些活动会无法进行。
那么所有活动可以排成一个可行线性序列，这个序列就是拓扑序列。
那么这个序列的实际意义是：
按照这个顺序，在每个项目开始时，能够保证它的前驱活动都已完成，从而使整个工程顺利进行。
回到我们这个例子中：
- 我们一眼可以看出来要先学 C1, C2，因为这两门课没有任何要求嘛，大一的时候就学呗；
- 大二就可以学第二行的 C3, C5, C8 了，因为这三门课的先修课程就是 C1, C2，我们都学完了；
- 大三可以学第三行的 C4, C9；
- 最后一年选剩下的 C6, C7。
这样，我们就把所有课程学完了，也就得到了这个图的一个拓扑排序。
注意，有时候拓扑序并不是唯一的，比如在这个例子中，先学 C1 再学 C2，和先 C2 后 C1 都行，都是这个图的正确的拓扑序，但这是两个顺序了。
所以面试的时候要问下面试官，是要求解任意解，还是列出所有解。
在这个图里的边表示的是一种依赖关系，如果要修下一门课，就要先把前一门课修了
在上面的图里，大家很容易就看出来了它的拓扑序，但当工程越来越庞大时，依赖关系也会变得错综复杂，那就需要用一种系统性的方式方法来求解了。
那么我们回想一下刚刚自己找拓扑序的过程，为什么我们先看上了 C1, C2?
因为它们没有依赖别人啊，也就是它的入度为 0.
- 入度：顶点的入度是指「指向该顶点的边」的数量；
- 出度：顶点的出度是指该顶点指向其他点的边的数量。
所以我们先执行入度为 0 的那些点，因此我们要先记录每个顶点的入度。因为只有当它的入度为 0的时候，我们才能执行它。
在刚才的例子里，最开始 C1, C2 的入度就是 0，所以我们可以先执行这两个。
那在这个算法里第一步就是得到每个顶点的入度。
（1）预处理得到每个点的入度
我们可以用一个 HashMap 来存放这个信息，或者用一个数组会更精巧。
拿到了这个之后，就可以执行入度为 0 的这些点了，也就是 C1, C2.
那我们把可以被执行的这些点，放入一个待执行的容器里，这样之后我们一个个的从这个容器里取顶点就好了。
至于这个容器究竟选哪种数据结构，这取决于我们需要做哪些操作，再看哪种数据结构可以为之服务。
那么首先可以把**[C1, C2]**放入容器中，
然后想想我们需要哪些操作吧！
我们最常做的操作无非就是把点放进来，把点拿出去执行了，所以可以用一个queue
其他的也行，放进来这个容器里的顶点的地位都是一样的，都是可以执行的，和进来的顺序无关，但何必非得给自己找麻烦呢？一个常规顺序的简简单单的 queue 就够用了。
然后就需要把某些点拿出去执行了。
当我们把 C1 拿出来执行，那这意味这什么？
答：意味着「以 C1 为顶点」的「指向其他点」的「边」都消失了，也就是 C1 的出度变成了 0.
如下图，也就是这两条边可以消失了。
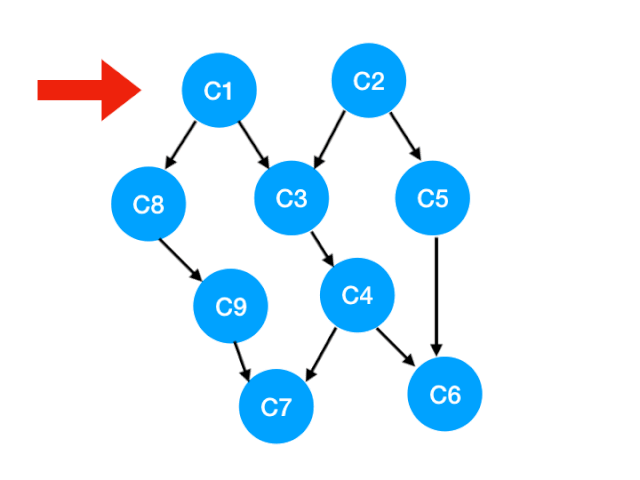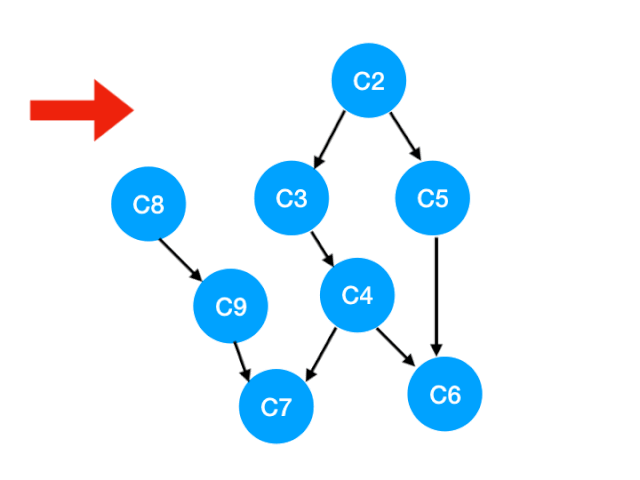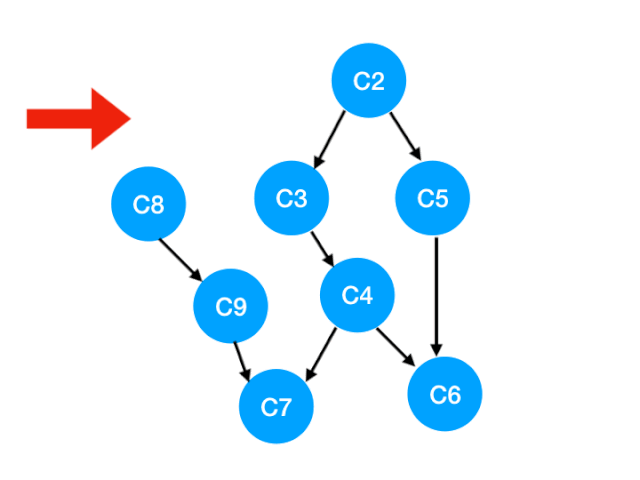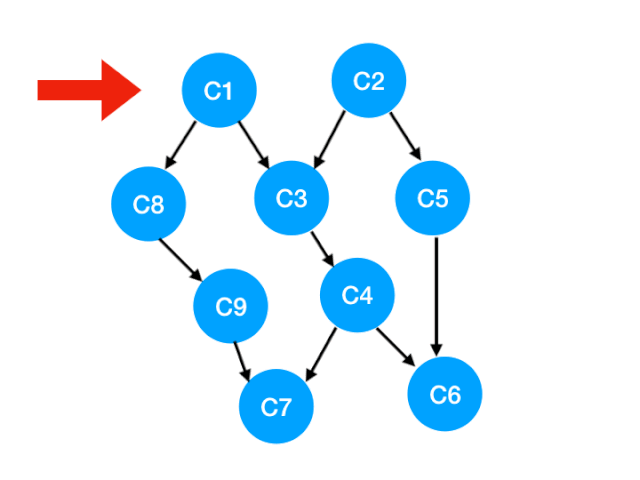
那么此时我们就可以更新 C1 所指向的那些点也就是 C3 和 C8 的 入度 了，更新后的数组如下：
那我们这里看到很关键的一步，C8 的入度变成了 0！
也就意味着 C8 此时没有了任何依赖，可以放到我们的 queue 里等待执行了。
此时我们的 queue 里就是：[C2, C8].
下一个我们再执行 C2
那么 C2 所指向的 C3, C5 的 入度-1，
更新表格：
也就是 C3 和 C5 都没有了任何束缚，可以放进 queue 里执行了。
queue 此时变成：[C8, C3, C5]
那么下一步我们执行 C8
相应的 C8 所指的 C9 的入度-1.更新表格：
那么 C9 没有了任何要求，可以放进 queue 里执行了。
queue 此时变成：[C3, C5, C9]
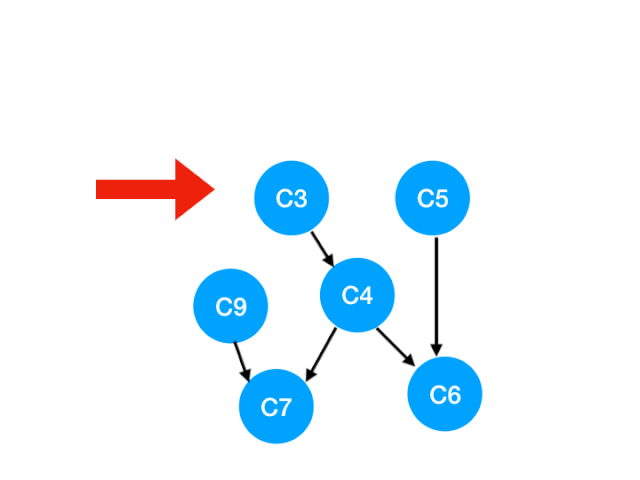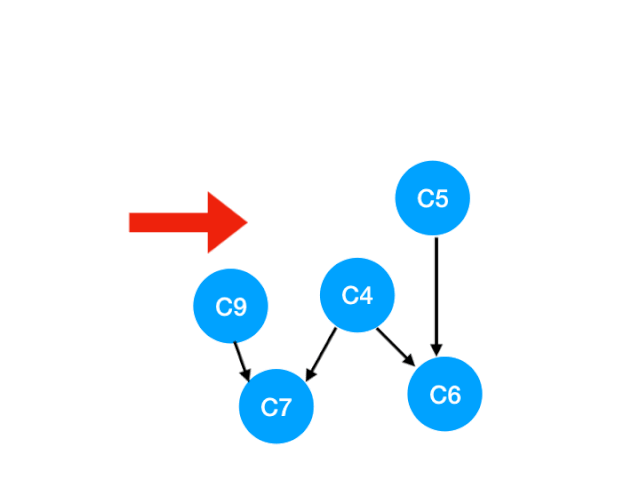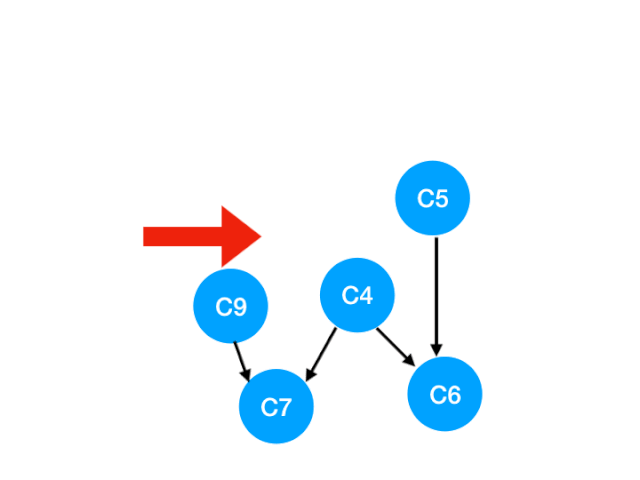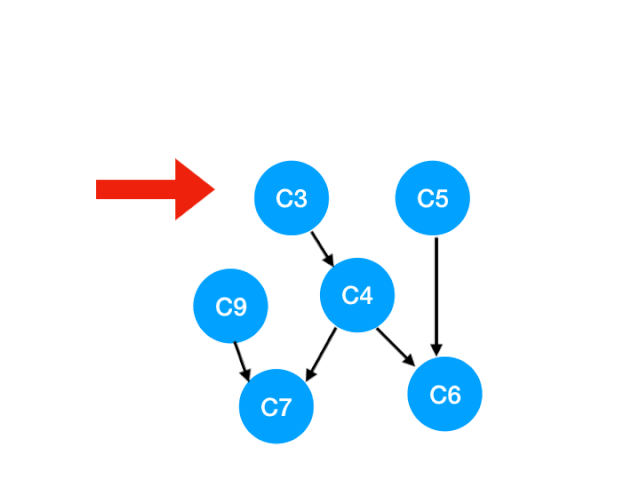
接下来执行 C3，
相应的 C3 所指的 C4 的入度-1.更新表格：
但是 C4 的入度并没有变成 0，所以这一步没有任何点可以加入 queue。
queue 此时变成 [C5, C9]
再执行 C5
那么 C5 所指的 C4 和 C6 的入度- 1.更新表格：
这里 C4 的依赖全都消失啦，那么可以把 C4 放进 queue 里了：
queue = [C9, C4]
Step6
然后执行 C9
那么 C9 所指的 C7 的入度- 1
这里 C7 的入度并不为 0，还不能加入 queue，
此时 queue = [C4]
接着执行 C4
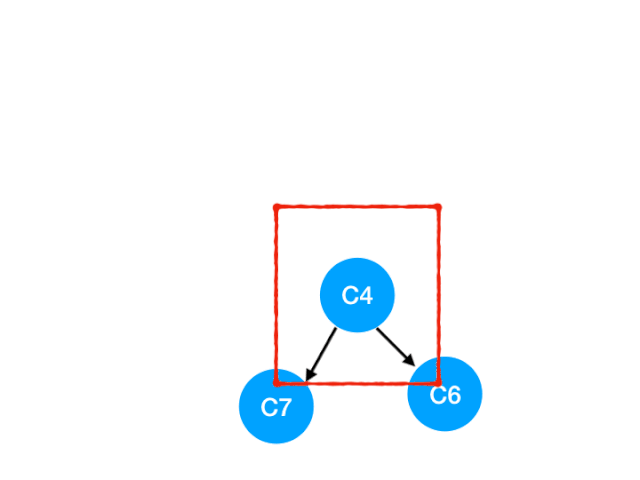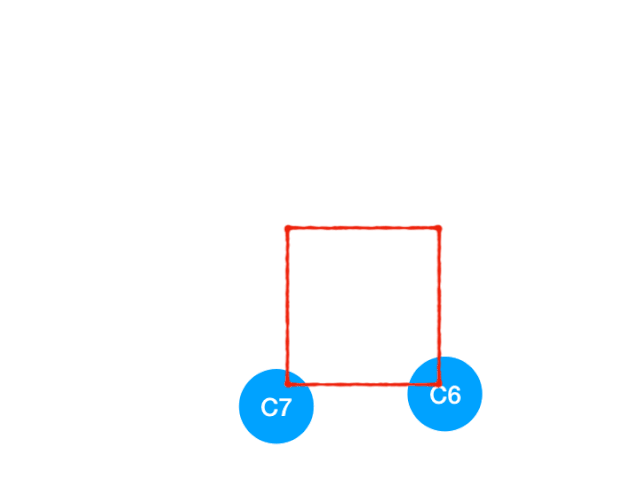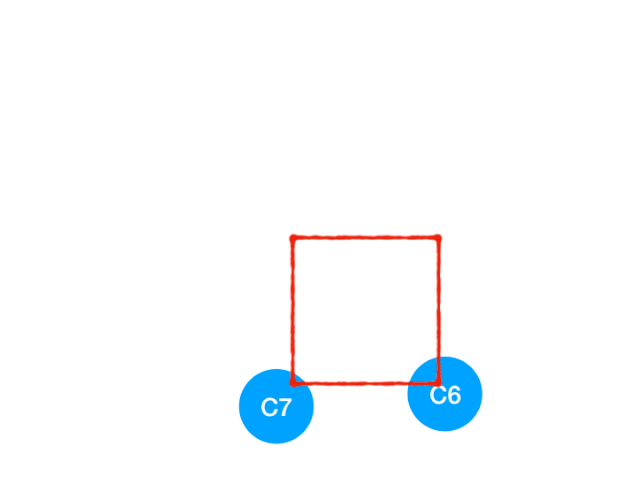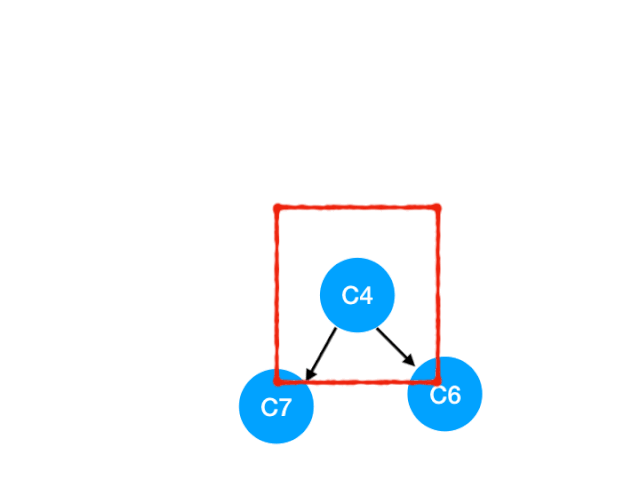
所以 C4 所指向的 C6 和 C7 的入度-1，更新表格：
C6 和 C7 的入度都变成 0 啦！！把它们放入 queue，继续执行到直到 queue 为空即可
时间复杂度
空间复杂度
#include