深度学习基础——PyTorch简介和Tensor张量详解

PyTorch具有悠久的历史，它的前身 Torch 是用Lua写的机器学习框架，后来受到 Facebook、NVIDIA (著名显卡生产厂商)、Uber 等大公司以及斯坦福大学、卡内基梅隆大学等著名高校的支持。下面，就让我们走进PyTorch的世界。

1 PyTorch安装

PyTorch 的安装非常简单。按照 PyTorch官网的说明，我们只需要选择操作系统、Python的版本，以及显卡 CUDA的版本，该网页就会提供一行命令，只需要在终端(Terminal，Windows系统就是命令行程序)输人相应的安装语句就可以安装了。例如，如果选择的操作系统是 Linux,包管理器是 Conda(需要事先安装 Anancoda)，Python版本 3.6，Cuda版本 8.0，则在命令行(终端)输人如下语句，就可以轻松安装好PyTorch:

conda install pytorch torchvision -c pytorch

另外，PyTorch官方提供了在 Windows 操作系统上安装 PyTorch的方法，对于大多数 Windows用户来说，这无疑提供了很大的便利。

由于网上PyTorch安装教程已经非常详细，这里就不再详细写，具体请参考Pytorch深度学习实战3-1：最新Windows/Ubuntu双系统Pytorch图文安装教程

2 初始PyTorch

PyTorch是在2017年1月由Facebook推出的。它是经典机器学习库Torch框架的一个端口，主要编程语言为python。PyTorch“曾经”的优点是动态图，现在的优点是开源代码和开源社区。

PyTorch是一个年轻的框架。2017年1月28日，PyTorch 0.1版本正式发布，这是Facebook公司在机器学习和科学计算工具Torch的基础上，针对Python语言发布的全新的深度学习工具包。PyTorch类似NumPy，并且支持GPU，有着更高级而又易用的功能，可以用来快捷地构建和训练深度神经网络。一经发布，PyTorch便受到深度学习和开发者们广泛关注和讨论。经过一年多的发展，目前PyTorch已经成为机器学习和深度学习者重要的研究和开发工具之一。

按照官方的说法，PyTorch 具有如下3个最关键的特性：

• 与Python完美融合（Pythonic）
• 支持张量计算（Tensor computation）
• 动态计算图（dynamic computation graph）

下面，我们分别对这些特性进行说明。

2.1 与Python完美融合

与Python完美融合是指PyTorch 是一个全面面向 Python 的机器学习框架，使用PyTorch与使用其他Python程序包没有任何区别。

与此形成鲜明对比的是TensorFlow，使用过的人都知道，TensorFlow会将一个深度学习任务分为定义计算图和执行计算的过程，而定义计算图的过程就好像在使用一套全新的语言。PyTorch就没有这个缺点，从定义计算图到执行运算都是一气呵成的，用户丝毫感受不到使用Python和PyTorch的区别。

2.2 张量计算

张量是PyTorch里的基本运算单位，与numpy的ndarray相同都表示一个多维的矩阵。与ndarray最大的区别在于Tensor能使用GPU加速，而ndarray只能用在CPU上。

PyTorch的运算单元叫做张量（tensor）。我们可以将张量理解为一个多维数组，一阶张量即为一维数组，通常叫做向量（vector）；二阶张量即为二维数组，通常叫做矩阵（matrix）；三阶张量即为三维数组；n阶张量即为n维数组，有n个下标。

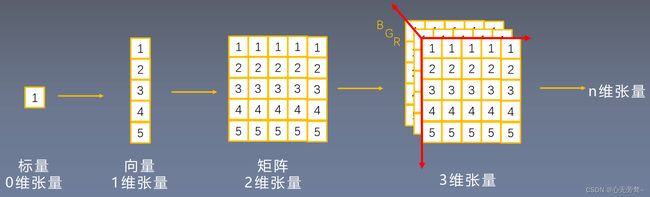
我们将一个张量每个维度的大小称为张量在这个维度的尺寸（size）。例如，在上图的三维张量中，它首先是由三个矩阵构成，所以它第一个维度的尺寸就是3；接下来，在每个维度上，它又是一个矩阵，这个矩阵有5行，因此它第二个维度的尺寸就是5；对于任意一行，它又是一个长度为5的向量，因此它第三个维度的尺寸就是5。如果我们将这个三阶张量看作一个立方体，那么3、5、5就分别是这个立方体的长、宽、高。

2.2.1 定义张量

下面，让我们来看看如何利用PyTorch 定义一个张量。首先，需要导人 PyTorch 的包，我们只需要在Jupyter Notebook 中输入以下命令即可:

# 导入PyTorch的包
import torch 

接下来，我们可以创建一个尺寸为$(5,3)$的二阶张量(也就是 5行3列的矩阵)。我们希望其中每个元素的数值是随机赋予的一个$[0,1]$区间中的实数，则只需要输人:

x = torch.rand(5,3)
x

其中，第二行的 x表示打印输出 的数值。系统的返回值如下( 每次执行数值都会不同):

tensor([[0.6645, 0.7023, 0.3701],
        [0.4142, 0.8930, 0.2642],
        [0.8537, 0.3351, 0.5520],
        [0.9519, 0.1935, 0.5348],
        [0.6088, 0.6822, 0.0975]])

可以看到系统打印输出了一个 5x3 的矩阵。

下面再看一个例子，创建一个尺寸为$(5,3)$、内容全是 1的张量，并打印输出：

y = torch.ones(5,3)
y

于是，系统输出如下：

tensor([[1., 1., 1.],
        [1., 1., 1.],
        [1., 1., 1.],
        [1., 1., 1.],
        [1., 1., 1.]])

接下来，让我们再创建一个三维(阶)的张量，尺寸为$(2,5,3)$，内容全是0：

z = torch.zeros(2,5,3)
z

系统输出如下：

tensor([[[0., 0., 0.],
         [0., 0., 0.],
         [0., 0., 0.],
         [0., 0., 0.],
         [0., 0., 0.]],

        [[0., 0., 0.],
         [0., 0., 0.],
         [0., 0., 0.],
         [0., 0., 0.],
         [0., 0., 0.]]])

可以看到，系统输出的实际上是两个尺寸为(5,3)、全是 0的张量，这就是 PyTorch 表示二维以上张量的方法。按照这样的方法，我们可以构造出任意维度的张量。

2.2.2 访问张量

接下来，让我们看看如何访问定义好的张量。其实上一个例子的输出已经提示我们可以使用如下方式访问张量中的元素：

# 打印z张量中的第一个元素
z[0]

这表示访问z 张量中的第一个元素(注意，张量的下标是从0开始的)。系统返回如下：

tensor([[0., 0., 0.],
        [0., 0., 0.],
        [0., 0., 0.],
        [0., 0., 0.],
        [0., 0., 0.]])

可以看到，它是一个尺寸为(5,3)的张量。那么，如果想访问x 张量中第 2行第 3列的数字，则可以使用下列 Python指令:

x[1,2]

系统返回：

tensor(0.2642)

最后，我们还可以使用切片 (slicing)的方法来访问张量，例如如果希望访问 x张量 中第 3列的全部元素，则可以输人：

x[:,2]

系统返回：

tensor([0.3701, 0.2642, 0.5520, 0.5348, 0.0975])

第一个维度下标用“：”表示所有的行，“：”相当于一个通配符。其实，熟悉 Python 的小伙伴应该已经发现了，PyTorch中的张量定义和访问方法与 Python中 NumPy数组的定义和访问没有什么区别，因此参考NumPy的各种语法和技巧来操作 PyTorch的张量就可以了。

2.2.3 张量的运算

PyTorch 中的张量还可像 NumPy 的多维数组一样完成各种各样的运算。例如，张量可以相加：

z = x + y
z

返回结果：

tensor([[1.6645, 1.7023, 1.3701],
        [1.4142, 1.8930, 1.2642],
        [1.8537, 1.3351, 1.5520],
        [1.9519, 1.1935, 1.5348],
        [1.6088, 1.6822, 1.0975]])

当然，要保证x和y的尺寸一模一样才能相加，这与线性代数里面的二维矩阵相加是一个道理。下面再来看看两个二维张量的矩阵乘法，其实这与两个矩阵相乘没有任何区别。这里需要调用 PyTorch 的 mm(matrix multiply)命令，它的作用就是矩阵相乘。

q = x.mm(y.t())
q

返回如下：

tensor([[1.7369, 1.7369, 1.7369, 1.7369, 1.7369],
        [1.5714, 1.5714, 1.5714, 1.5714, 1.5714],
        [1.7408, 1.7408, 1.7408, 1.7408, 1.7408],
        [1.6802, 1.6802, 1.6802, 1.6802, 1.6802],
        [1.3885, 1.3885, 1.3885, 1.3885, 1.3885]])

注意，根据矩阵乘法的基本规则，输出的张量尺寸大小转变为$(5,5)$。其中，y.t 表示矩阵y的转置。因为x的尺寸为$(5,3)$，y的尺寸为$(5,3)$，而根据矩阵的乘法规则，第一个张量第二个维度的尺寸必须和第二个张量第一个维度的尺寸相等才能相乘，因此，将y 转置之后得到 y.t 的尺寸是$(3,5)$，才可以和相乘。学过线性代数的小伙伴们应该十分熟悉，这就是矩阵的转置，所以学到目前看来，要想入门深度学习，还是需要一定的数学基础，其中不仅包括线代，还有概率论和数理统计等等。不过大家不用惊慌，我们可以一步一步地慢慢学习。

张量的基本运算还有很多，包括换位、索引、切片、数学运算、线性算法和随机数等，详见PyTorch官方文档，在此不再赘述。

2.2.4 张量与NumPy数组之间的转换

既然 PyTorch 的张量与 NumPy 的多维数组如此之像，那么它们之间应该可以自由转换PyTorch提供了NumPy和张量之间简单的转换语句。

从NumPy到张量的转换为from_numpy(a)，其中a为一个NumPy数组。反过来，从张量到Numpy的转换可以使用a.numpy()，其中a为一个PyTorch张量。

例如，如果有：

import numpy as np

x_tensor = torch.randn(2,3)
y_numpy = np.random.randn(2, 3)

x_tensor 是一个尺寸为$(2,3)$的随机张量，y_numpy 是一个尺寸为$(2,3)$的随机矩阵。randn的意思是创建一个满足正态分布的随机张量或矩阵(rand是均匀分布的随机张量或矩阵)。

那么，我们可以将张量转化为NumPy：

x_numpy = x_tensor.numpy()

也可以将 NumPy转化为张量：

y_tensor = torch.from_numpy(y_numpy)

除了这种直接转换，大多数时候还需要按照类型进行转换。例如，如果 a 是一个 float 类型的Numy数组,那么可以用torch.FloatTensor(a)将 a 转化为一个float类型的张量。与此类似，如果a是一个int类型的NumPy数组，那么我们可以用torch.LongTensor(a)将a转化为一个整数类型的张量。

2.2.5 GPU上的张量计算

学到现在，相信很多小伙伴应该有一个疑问吧，既然很多 PyTorch中的张量运算都与 Numy 中的数组运算一样,那么 PyTorch 为什么还要发明张量而不直接用 NumPy的数组呢?

答案就在于，PyTorch 中的张量是可以在GPU 中计算的，这大大地提高了运算速度，而NumPy数组却不能。

首先，要完成GPU上的运算，需要确认你的计算机是否已经安装了GPU并且可以正常操作。可以用如下方法进行验证:

torch.cuda.is_available()

如果返回True就表明你的GPU已经正常安装，否则将无法使用 GPU。当确认可以使用之后你只需要将定义的张量放置到 GPU上即可。例如，将 x、y 放到 GPU 上，你只需要输人如下代码即可：

if torch.cuda.is_available():
    x = x.cuda()
    y = y.cuda()
    print(x+y)

返回如下：

tensor([[1.6645, 1.7023, 1.3701],
        [1.4142, 1.8930, 1.2642],
        [1.8537, 1.3351, 1.5520],
        [1.9519, 1.1935, 1.5348],
        [1.6088, 1.6822, 1.0975]], device='cuda:0')

注意，最后一行多出来的 cuda:0 表明当前这个输出结果 x+y 是存储在 GPU上的。

当然，你的计算机版本设置也可能不支持 GPU，如果你希望获得 GPU 资源，可以考虑在云服务器平台上运行。

我们也可以将已存储在 GPU上的变量再“卸载”到 CPU 上，只需要输人以下命令即可：

x = x.cpu()

如果你的计算机本来就没有 GPU，那么执行上述语句就会出错，所以最好是在前面加上if torch.cuda.is_available()进行判断。
即：

if torch.cuda.is_available():
	x = x.cpu()

PyTorch的第三特性动态计算图我们下次再详细讲解~