广度优先搜索和深度优先搜索

---

1. 前言

    深度优先搜索算法的基础是递归，如果你对递归还不熟悉的话，建议先去看看递归的概念，做一些递归的练习题，也可以看我之前写的递归的文章：递归算法详解

---

2. 广度优先搜索和深度优先搜索

     在这篇文章中同时总结下广度优先搜索和深度优先搜索，这两种算法是针对 “图” 的遍历方法，当然这里的图是指的是广义上的图，可以是实际的图，可以是N叉树，甚至可以是二维矩阵。其中深度优先搜索是每一次按照一个方向进行穷尽式的搜索，当该方向上的搜索无法继续往前的时候，这时就退回到上一步，换一个方向继续搜索。而广度优先走是按照层次由近及远的进行搜索，在当前层次所有可及节点都搜索完毕后才会继续往下搜索，其本质就是寻找从起点到终点的最短路径。下面以二叉树的遍历过程说明两种搜索算法之间的区别：

1）深度优先搜索

    这种搜索方法会按照一个方向进行穷尽搜索，所以首先会一直搜索左子树，直到某个节点没有左子树为止，接着换个方向搜索右子树，图示如下：

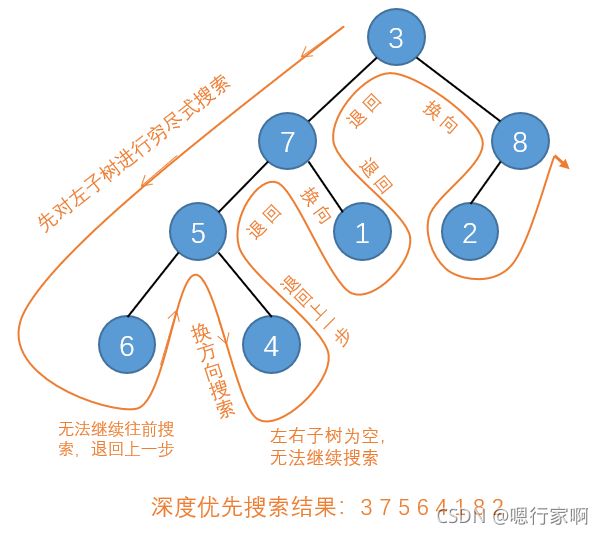
2）广度优先搜索

    与深度搜索不同的是这种搜索的方式总是按照层次进行的，当前层所以节点都访问过后才会继续往下，图示如下：

---

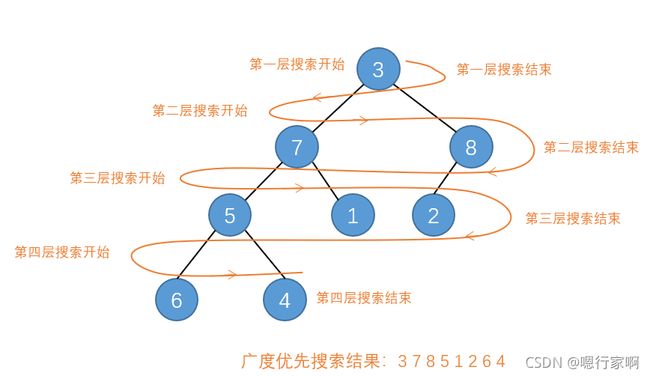
3. 深度优先搜索算法框架

void DFS(当前节点){
    对当前节点的访问;`在这里插入代码片`
    标记当前节点为已访问;
    for(下一节点 : 当前节点的邻接列表){
        剪枝(如果下一节点已经访问过就跳过);
        DFS(下一节点);
    }
}

1）二叉树深度优先搜索模板

//二叉树前序DFS搜索
void DFS(TreeNode* root){
    if(root == nullptr) return;
    cout << root->val << " "; //输出当前节点
    //这里不需要标记当前节点为已访问，因为二叉树不会往回走
    DFS(root->lchild); 
    DFS(root->rchild); 
}

调整输出节点的位置，还能得出另外两种二叉树DFS遍历：

//二叉树中序DFS搜索
void DFS(TreeNode* root){
    if(root == nullptr) return;
    DFS(root->lchild);
    cout << root->val << " "; //输出当前节点
    DFS(root->rchild);
}

//二叉树后序DFS搜索
void DFS(TreeNode* root){
    if(root == nullptr) return;
    DFS(root->lchild);
    DFS(root->rchild);
    cout << root->val << " "; //输出当前节点
}

2）图深度优先搜索模板

vector<int> visited; //用来标记已访问节点
void DFS(Graph *G, int v){
    cout << v << " "; //输出当前节点
    visited[v] = 1; //标记当前节点为已访问
    for(int w = 0; w < G->vexnum; w++){
        if(!visited[w])
           DFS(G, w);
    }
}

3）二维矩阵深度优先搜索模板

int m = matrix.size(); //行数
int n = matrix[0].size();  //列数
vector<vector<int>> visited(m, vector<int>(n, 0)); //用来标记已经访问过的节点
int directions[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}}; //行进方向


void DFS(vector<vector<int>> &matrix, int x, int y){
    if(matrix[x][y] == target)
        return;
    visited[x][y] = 1; //标记当前节点为已访问
    
    for(int i = 0; i < 4; i++){
        int new_x = x + directions[i][0];
        int new_y = y + directions[i][1];
        	//这里一定要把visites[new_x][new_y]放在最后，因为计算后的new_x和new_y值有可能已经超过visited的下标访问范围
        	if(new_x < 0 || new_x >= m || new_y < 0 || new_y >= n || visited[new_x][new_y]) continue; 
            	DFS(matrix, new_x, new_y);
    }
}

---

4. 广度优先搜索算法框架

    首先需要明确的就是，广度优先搜索是按照层次遍历的，所以广度优先搜索不能像深度优先搜索一样使用递归来实现，广度优先搜索需要申请辅助队列来记录下一层需要遍历的节点

1）单源广度优先搜索

    从一个起点出发到一个终点结束

//单源的广度优先搜索
int BFS(elemType start, elemType target) {
    queue<elemType> q; //申请辅助队列
    set<elemType> visited; //标记已访问过的，避免走回头路
    q.push(start); //起点入队列
    visited.insert(start); //标记起点
    int step = 0; //记录步数
    while (!q.empty()) {
        int sz = q.size(); //每一层的元素个数
        for (int i = 0; i < sz; i++) {
            elemType cur = q.pop(); //获得队列中的元素
            if (cur == target) { //判断是否需要结束搜索
                return step;
            }
            for (elemType x : cur.neighbor()) { //确定下一层需要搜索的节点
                if (visited.find(x) == visited.end()) {
                    q.push(x);
                    visited.insert(x);
                }
            }
        }
        step++; // 步数加一
    }
}

2）多源广度优先搜索

    顾名思义，多源广度优先搜索的意思是可以从多个起点开始向外进行搜索，是一种扩散式的搜索方法，如下图所示，图中值为0的点表示起点，则与每个0上下左右相邻的节点值就为1，同样与每个1上下左右相邻的节点值就为2。

vector<vector<int>> mulBFS(vector<vector<int>>& mat) {
    int m = mat.size();
    int n = mat[0].size();
    vector<vector<int>> dist(m, vector<int>(n, 0)); //记录每个位置上的步数
    vector<vector<int>> visited(m, vector<int>(n, 0)); //用来标记是否访问过
    queue<pair<int, int>> q;
    //第一步就是将多个源点按顺序入队列
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            if (mat[i][j] == 0) {
                q.push(pair<int, int>(i, j));
                visited[i][j] = 1;
            }
        }
    }
    while (!q.empty()) {
        int sz = q.size();
        for (int i = 0; i < sz; i++) {
            auto [x, y] = q.front();
            q.pop();
            for (int j = 0; j < 4; j++) {
                int new_x = x + directions[j][0];
                int new_y = y + directions[j][1];
                if (new_x < 0 || new_x >= m || new_y < 0 || new_y >= n ||  visited[new_x][new_y]) continue;
                q.push(pair<int, int>(new_x, new_y));
                visited[new_x][new_y] = 1;
                dist[new_x][new_y] = dist[x][y] + 1;
            }
        }
    }
}

[注]：上述的两种广度优先搜索中我们给出了两个记录步长的方式，第一种是设置一个step，然后每向前一步就step++，这种比较适合单源的广度优先搜索；第二种是设置一个辅助dist数组，记录所有节点的距离，然后通过 dist[newNode] = dist[oldNode]+1 进行更新，这种比较适合多源的广度优先搜索。

3）双向广度优先搜索

    广度优先搜索是求图中最短路径的方法，一般是从某个起点出发，一直穷举直到碰到某个结束值(也就是目标值)，这样的搜索过程就是单向的搜索，而有的题目即会提供起点位置，也会提供终点的位置，这样的题目可以采用双向的广度优先搜索， 当发现某一时刻两边都访问过同一顶点时就停止搜索。比如下面这个题目：
    LeetCode 127. 单词接龙：在本题目中起始单词 beginword 和 结束单词 endword均已经给出，因此可以采用双向的广度优先搜索。
双向广度优先搜索算法流程：
    1. 需要定义两个辅助队列，一个放前向搜索时的节点，一个存放逆向搜索时的节点
    2. 查看两个辅助队列中是否有相同的元素，以判断搜索是否结束
    3. 轮流进行搜索，也就是前向搜索进行一次后紧跟着就要做一次逆向搜索

int BFS(string beginWord, string endWord, vector<string>& wordList) {
    unordered_set<string> wordSet(wordList.begin(), wordList.end());
    if (wordSet.find(endWord) == wordSet.end()) return 0;
    unordered_set<string> q_start, q_end, visited; //双向搜索要定义两个set作为辅助队列
    q_start.insert(beginWord);
    q_end.insert(endWord);
    int step = 1;
    while (!q_start.empty() && !q_start.empty()) {
        unordered_set<string> temp; //定义一个temp为了将q_start将q_end交换
        for (string cur : q_start) {
            cout << cur << " ";
            if (q_end.find(cur) != q_end.end()) return step; //查看两个队列中是否有相同的元素，相同则结束遍历
            //这一步很关键，单向BFS中是在新节点入队的同时加入访问数组，这里不行，因为我们结束查找的条件就是两个队
            //列中是否有相同的条件，如果在新节点入队的同时加入访问数组，两个队列中就一定不会有相同的元素，因此要在判断后加
            visited.insert(cur); 
            for (int k = 0; k < cur.size(); k++) {
                string newWord = cur;
                for (int i = 0; i < 26; i++) {
                    newWord[k] = i + 'a';
                    if (wordSet.find(newWord) != wordSet.end() &&  visited.find(newWord) == visited.end()) {
                        temp.insert(newWord);
                    }
                }
            }
        }
        step++;
        //交换搜索的方向
        q_start = q_end; 
        q_end = temp;
    }
    return 0;
}