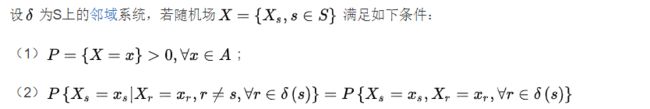马尔可夫链在人工智能中的应用

前言

本文以马尔可夫链在人工智能中的应用为例，从概念介绍、马尔克夫链的常用模型、马尔可夫链的具体应用这三个方面阐述，并通过简述马尔科夫链的发展历史，展现了在人工智能领域中数学思维的重要性。注意，由于作者的学识问题，很多方面可能无法进行深层次的探究，只能从浅层上来进行分析。并且，文章中主要做的是资料的整合、加工工作，因此有许多需要参考引用的资料文献。本文已在末尾处附有参考的资料，在这里，我对所引用的资料的作者表达真挚的谢意！

【关键词】 人工智能 马尔可夫链 强化学习

正文

零. 什么是马尔可夫链？

1. 从古诗文之美到数学思维之妙

“悟已往之不谏，知来者之可追”，这是陶渊明的诗，其中的诗文之美令人陶醉其中。但是，如此如诗如画的田园风光里，正藏着值得深思的哲学思想——过去的事已经无法挽回，想要得到将来，就必须要把握现在。

2. 这就是马尔科夫链

马尔可夫链（Markov Chain, MC）是概率论和数理统计中具有马尔可夫性质（Markov property）且存在于离散的指数集（index set）和状态空间（state space）内的随机过程（stochastic process）。

马尔可夫性质——数学公式版

马尔可夫性质——能听懂版

就是如同陶渊明所说的，在给定当前知识或信息的情况下，过去对于预测将来是无关的。这就是马尔可夫性质。 具有这样的性质的一个离散的序列（序列中的状态可以为任意），就是马尔科夫链。

3. 马尔可夫链的其他相关数学概念

状态空间：这些变量的范围，即它们所有可能取值的集合，被称为状态空间，而集合中每个元素的值则称为在时间n的状态。

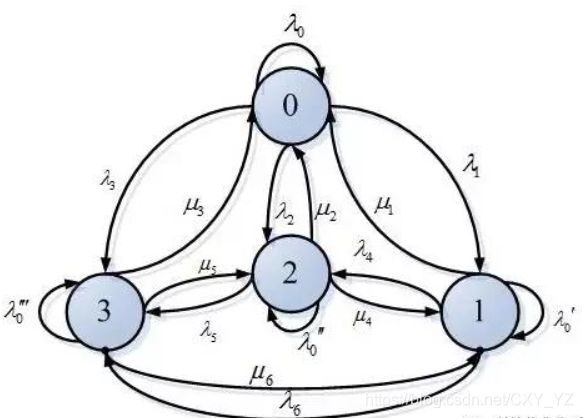
转移概率：状态的改变叫做转移，与不同的状态改变相关的概率叫做转移概率。可以将状态转移概率列出成为一个状态转移矩阵。

正定性：在状态转移矩阵中，每个状态转移概率皆为正数。

有限性：状态转移阵中的每一行状态转移阵中每行相加均为1。

图中圈1、圈2、圈3即为状态，λ1、λ2为状态转移概率

壹. 马尔可夫链的历史

马尔科夫链其实是马尔科夫过程在状态与概率皆离散的情况下的特殊情况，而在马尔科夫过程的研究中，不少科学家前赴后继奉献了许多成果。

提出概念

马尔科夫链的概念由俄国数学家A.A.马尔可夫于1907年提出。

理论基础

1931年至1951年，Α.Η.柯尔莫哥洛夫发表了的《概率论的解析方法》以及伊藤清建立的随机微分方程的理论，为马尔可夫过程的研究奠定了理论基础。

规定领域，深入研究

1954年前后，W.费勒将半群方法引入马尔可夫过程的研究。确定了流形上的马尔可夫过程、马尔可夫向量场等都是正待深入研究的领域。

50年代初，角谷静夫和J.L.杜布等发现了布朗运动与偏微分方程论中狄利克雷问题的关系，后来G.A.亨特研究了相当一般的马尔可夫过程（亨特过程）与位势的关系。

1956年，有人找到马尔可夫过程不是强马尔可夫过程的例子。但是，马尔可夫过程理论的进一步发展表明，强马尔可夫过程才是马尔可夫过程真正研究的对象。

马尔科夫链模型在人工智能的应用中的历史

马尔可夫决策模型与机器学习

1957年，美国学者Richard Bellman通过离散随机最优控制模型首次提出了离散时间马尔可夫决策过程 。1960年和1962年，美国学者Ronald A. Howard和David Blackwell提出并完善了求解MDP模型的动态规划方法 。

随着Watkins (1989)在发表后得到了机器学习领域的关注，MDP也由此作为强化学习问题的常见模型而得到应用 。

隐马尔科夫过程模型与模式识别等方面

自20世纪80年代以来，HMM被应用于语音识别，取得重大成功。到了90年代，HMM还被引入计算机文字识别和移动通信核心技术“多用户的检测”。HMM在生物信息科学、故障诊断等领域也开始得到应用。

贰. 马尔科夫链的模型（分类）

显隐分类

通过状态的类型，马尔可夫模型可以分为马尔可夫显性模型（VMM）和马尔可夫隐性模型(HMM)两类：

显马尔可夫模型：状态确定，状态转移概率确定的模型
隐马尔可夫模型：含有一个未知参数的马尔科夫模型，注意，这是一个**双重随机过程！包含马尔可夫链以及一个一般随机过程。**一般随机过程即指向该未知参数的随机性。

隐马尔可夫的模型表达

可以使用一个五元组表达：（S,O,Π,A,B）

隐马尔可夫模型的重要内容

隐马尔科夫模型是贝叶斯网络的一种最简单的呈现在隐马尔可夫模型中，状态是不直接可见的，但输出依赖于该状态下，是可见的。每个状态通过可能的输出记号有了可能的概率分布。因此，通过一个HMM产生标记序列提供了有关状态的一些序列的信息。注意，“隐藏”指的是，该模型经其传递的状态序列，而不是模型的参数；即使这些参数是精确已知的，我们仍把该模型称为一个“隐藏”的马尔可夫模型。隐马尔可夫模型以它在时间上的模式识别所知，如语音，手写，手势识别，词类的标记，乐谱，局部放电和生物信息学应用。

按照应用分类

除了马尔可夫隐性模型的应用外，马尔科夫链还在许多领域起着重要作用。其中，较为重要的是，马尔可夫随机场以及马尔可夫决策过程。

马尔可夫随机场

马尔科夫随机场指的是蕴含马尔可夫性质的这样一种特殊随机场。（当给每一个位置中按照某种分布随机赋予相空间的一个值之后，其全体就叫做随机场）

或者我们可以打一个生动的比方，场就像一张棋盘，位置就相当于一个个棋格，相空间就是所有可以落的子的集合。我们可以在每个棋格上随意的下棋，这就是随机场。马尔可夫随机场指的就是，每一个下棋的子只与旁边的棋格有关。

马尔可夫随机场的数学描述如下

马尔可夫随机场的作用

马尔可夫随机场常常用于描述一个不确定性问题。求解马尔科夫随机场描述的不确定性问题，利用统计决策、估计理论、贝叶斯理论，将道路场景的先验知识用先验分布模型表示，使用最大后验估计作为道路场景分割的标准。

马尔可夫决策过程

马尔可夫决策过程（Markov Decision Process, MDP）是序贯决策（sequential decision）的数学模型，用于在系统状态具有马尔可夫性质的环境中模拟智能体可实现的随机性策略与回报

在强化学习中，马尔科夫决策过程起到重要作用。强化学习问题在本质上，要求环境的下个状态与所有的历史信息，包括状态、动作和奖励有关，但在建模时采用马尔可夫假设可以在对问题进行简化的同时保留主要关系。此时，环境的单步就可以对其未来的状态进行预测。因此即便一些环境的状态信号不具有马尔可夫性，其强化学习问题也可以使用MDP建模。

叁. 马尔科夫链的应用

HMM模型在中文分词中的应用

在语音识别的功能中，为我们说的话断句、分词是一项重要工作，而语音识别这一项人工智能后就隐藏着HMM模型的思想。

首先输入一句话，我们会根据文字的不同词性进行分词。在这里，每一个文字的输入对应一个状态值。状态值集合为(B,M,E,S)，分别代表的是该字在词语中的位置。
B代表的是该字作为某个词的开始，M代表该字是某个词中的中间字，E代表词语的结束字，S代表单字成词。

例如，“小明硕士毕业于中国科学院计算所” 对应 BEBEBMEBEBMEBES

通过切词规律：
B后面只可能接(M or E)，不可能接(B or S)。而M后面也只可能接(M or E)，不可能接(B, S)。
而我们的目标就是求出这样的一个字符串BBSSS…，通过输入的参数。

可以划分为BE/BE/BME/BE/BME/BE/S

其次我们将确定五元组，五元组如下所示

上面只介绍了五元组中的两元【StatusSet, ObservedSet】，下面介绍剩下的三元【InitStatus, TransProbMatrix, EmitProbMatrix】。

这五元的关系是通过一个叫Viterbi的算法串接起来， ObservedSet序列值是Viterbi的输入， 而StatusSet序列值是Viterbi的输出， 输入和输出之间Viterbi算法还需要借助三个模型参数， 分别是InitStatus, TransProbMatrix, EmitProbMatrix。（Viterbi算法在此不作深入介绍）

InitStatus矩阵
对所有（B,E,M,S）出现的频率值取对数之后的结果。(可以让概率相乘的计算变成对数相加)（4x1矩阵）
TransProbMatrix矩阵
马尔科夫链最大的特点就是当前T=i时刻的状态Status(i)，只和T=i时刻之前的n个状态有关。有个“有限历史性假设”，也就是马尔科夫链的n=1，Status(i)只和Status(i-1)相关。
矩阵的横坐标和纵坐标顺序是BEMS x BEMS。(数值是概率求对数后的值，同上)（4x4矩阵）

EmitProbMatrix矩阵
发射概率本质上是一个条件概率。

最后，代入五个参数，使用Viterbi算法得出最终结果。

HMM在语音识别中的应用

语音识别中也包含了大量的HMM模型的应用。


同理，确定好隐含参数，并代入模型中的参数，使用Viterbi算法求解即可。

肆. 数学思维的体现

马尔科夫链并非只是一个单纯的数学公式，在马尔科夫链中蕴含了深刻的对于规律的建模，而这也是数学上第一次对于现在、过去、未来关系之间清晰的建模，是一个具体而有用的数学思维。计算机学科中数学思维应用同样不在少数，比如贝叶斯模型、大数定律等。
许多人工智能界的大佬都曾发表过类似的言论，“数学是人工智能的基石”。是的，人工智能的本质上既是对于人思维的模仿、建模。而数学思维中蕴含的类似思维逻辑、建模方法，都是建模中必不可少的一部分。
因此，清晰的学习人工智能的路径即摆在了我们的眼前，夯实数学基础、把握数学规律就是学习人工智能的关键。学习人工智能，路阻且长，今有此文，与诸君共勉。

参考资料

[1]Sutton, R.S. and Barto, A.G. ．Reinforcement learning: An introduction (Second edition)：MIT press，2018：Chapter 1-3
[2]https://baike.baidu.com/item/%E9%A9%AC%E5%B0%94%E5%8F%AF%E5%A4%AB%E5%86%B3%E7%AD%96%E8%BF%87%E7%A8%8B/5824810#reference[1]-1850374-wrap
[3]隐马尔可夫模型——卢子墨 https://blog.csdn.net/lukabruce/article/details/82380511
[4]李龙龙．道路场景中的马尔科夫随机场方法研究：南京理工大学，2013
[5]https://rrl360.com/boke/14032
[6]https://tech.hqew.com/fangan_2017381
[7]https://mp.ofweek.com/ai/a945673920186
[8]https://baike.baidu.com/item/%E9%A9%AC%E5%B0%94%E5%8F%AF%E5%A4%AB%E9%9A%8F%E6%9C%BA%E5%9C%BA/3287733