四、二叉树

树是常用的数据存储方式，由于树中存在大量的指针结构，所以树的有关操作相对来说是比较难的。

一、 树的定义

这里用二叉树来举例子

使用结构体的方式实现二叉树:
struct BinaryTreeNode {
	int data;
	BinartTreeNode* left;
	BinartTreeNode* right;
};

使用类的方式实验二叉树：
class BinaryTreeNode {
public:
	int data;
	BinaryTreeNode *left;
	BinaryTreeNode* right
	BinaryTreeNode(int value) : data(value), left(nullptr), right(nullptr) { }
};

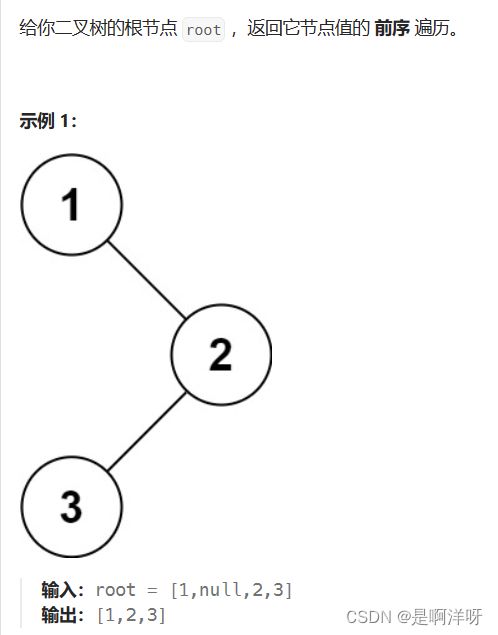
二、二叉树的前、中、后序遍历

前序遍历：根左右
中序遍历：左跟右
后序遍历：左右根

2.1 前序遍历

2.1.1 递归形式实现前序遍历

class Solution{
public:
	void preorder(TreeNode *root, vector &res){
		if (root == nullptr){
			return;
		}
		res.push_back(root->val);
		preorder(root->left, res);
		preorder(root->right, res);
	}
	vector preorderTraversal(TreeNode *root){
		vector res;
		preorder(root, res);
		return res;
	}
};

2.1.2 迭代形式实现前序遍历

class Solution{
public:
    vector preorderTraversal(TreeNode* root){
        vector res;
        if (root == nullptr){
            return res;
        }
        stack stk;//创建一个栈
        TreeNode* node =root;//创建一个树节点
        while (!stk.empty() || node != nullptr){
            while(node != nullptr){//只要节点有左子树，就进行这一步骤
                res.emplace_back(node->val);//节点的值存入res
                stk.emplace(node);//节点存入栈中
                node = node->left;
            }
            node = stk.top();
            stk.pop();
            node = node->right;
        }
        return res;
    }
};

2.2 中序遍历

2.2.1 递归形式的中序遍历

先找左子树，左子树没有了，存储当前节点，再找右子树

class Solution {
public:
    void midorder(TreeNode *root, vector &res){
        if (root == nullptr){
            return;
        }
        midorder(root->left, res);
        res.push_back(root->val);
        midorder(root->right, res);
    }
    vector inorderTraversal(TreeNode* root) {
        vector res;
        midorder(root, res);
        return res;
    }
};

2.2.2 迭代形式的中序遍历

class Solution{
public:
    vector inorderTraversal(TreeNode* root){
        vector res;
        if(root == nullptr) return res;
        stack stk;
        TreeNode* node = root;
        while (!stk.empty() || node != nullptr){
            while (node != nullptr){
                stk.emplace(node);
                node = node->left;
            }
        node = stk.top();
        stk.pop();
        res.push_back(node->val);
        node = node->right;
        }
        return res;
    }
};

2.3 后序遍历

2.3.1 递归形式的后序遍历

class Solution {
public:
    void lastorder(TreeNode* root, vector &res)
    {
        if (root==nullptr) return;
        lastorder(root->left, res);
        lastorder(root->right, res);
        res.push_back(root->val);
    }
        vector postorderTraversal(TreeNode*root) 
    {
        vector res;
        lastorder(root, res);
        return res;
    }
};

2.3.2 迭代形式的后序遍历

class Solution {
public:
    vector postorderTraversal(TreeNode *root) {
        vector res;
        if (root == nullptr){
            return res;
        }
        stack stk;
        TreeNode *prev = nullptr;
        while (root != nullptr || !stk.empty()){
            while (root != nullptr){
                stk.emplace(root);
                root = root->left;
            }
            root = stk.top();
            stk.pop();
            if (root->right == nullptr || root->right == prev){
                res.emplace_back(root->val);
                prev = root;
                root = nullptr;
            }
            else{
                stk.emplace(root);
                root = root->right;
            }
        }
        return res;
    }
};

2.4 根据前序遍历构造二叉搜索树

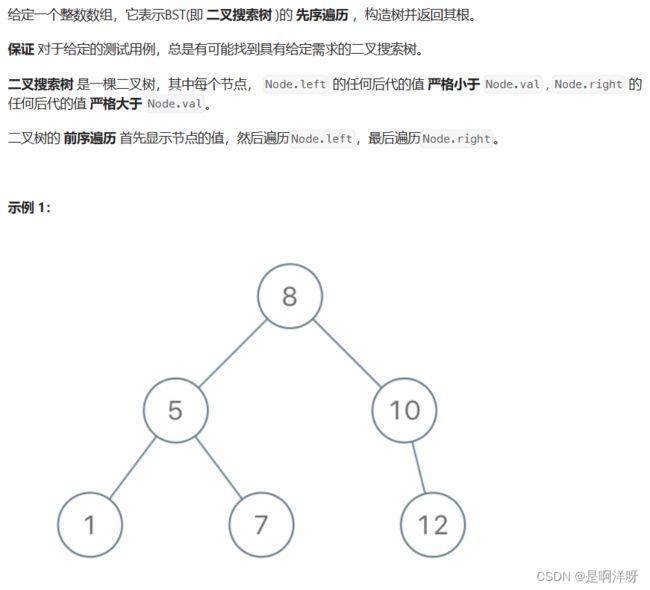
这道题目是有一些难度的，首先需要弄明白原理，根据题目的分析，首先第一个节点是根节点(称其为root)，第一个比根节点大的，就是根节点的右子树(称其为Rchild)，那么root和Rchild之间的成员，一定是根节点左子树或左子树的孩子。其中的第一个，就是根节点的左子树。
那么根据上面的思想，可以写出伪代码

TreeNode* fun(vector& preorder, int left, int right){
	if (left>right) return nullptr;
	int root = preorder[left];
	int mid = left;
	for(; mid<=right; mid++){
		if(preorder[mid]>root) break;
	}
	TreeNode *node = new TreeNode(root);
	node->left = fun(vector& preorder, int left+1, int mid-1)
	node->right = fun(vector& preorder, int mid, int right)
	return node;
}

上面的代码还是挺难想的，必须清楚的考虑边界条件才能写对，了解一下吧