tarjan算法、割点和割桥，

tarjan算法是求一个图的强连通子图的

dfn[u]数组记录的这个节点入树的时间
low[u]数组记录的是以u为根节点的子树中最小的时间戳

步骤是：通过搜索不断的更新low和dfn数组，
这个过程其实很好相同，对于一个联通分量，我们默认为我们在dfs深搜遍历到的第一个节点就是这个联通分量的根节点，那么也就是dfn最小的节点，这个联通分量的其他节点必定和这个联通分量的一些节点形成环，dfn与low不相等，所以这个算法思想的核心就是求dfn与low。一般搜索到没路的时候在回溯的过程中就是找根节点的时候，根节点后面压入栈的就是和他同一个联通分量了
，那么就回溯找根节点（dfn[u]==low[u])，并把这个强连通图给记录下来；

const int maxn=1e5;
int dfn[maxn],low[maxn],head[maxn],vis[maxn];
int tot,cnt,num;
struct node{
	int v,nex;
}edge[maxn];

void init()
{
	fill(vis,vis+maxn,0);
	fill(dfn,dfn+maxn,0);
	fill(low,low+maxn,0);
	fill(head,head+maxn,-1);
	tot=0;
}

void addedge(int u,int v)
{
	edge[++tot]={v,head[u]};
	head[u]=tot;
}

void tarjan(int u)
{
	st.push(u);
	vis[u]=1;
	dfn[u]=low[u]=++cnt;
	for(int i=head[u];i!=-1;i=edge[i].nex)
	{
		int v=edge[i].v;
		
		if(!dfn[v])//还未遍历过无dfn,low,先搜在更新
		{
			tarjan(v);
			low[u]=min(low[u],low[v]);
		}
		else if(vis[v])//已经遍历过了，而且还没有给它确定一个联通分量
		{
			low[u]=min(low[u],dfn[v]);//这里也可以low[v],但为了和下面割点同意，还是写成dfn好，写成low会出问题
		}				
	}
	
	if(dfn[u]==low[u])
	{
		num++;
		while(1)
		{
			int x=st.top();
			vis[x]=0;
			st.pop();
			belong[x]=num;
			if(x==u) break;
		}
	}	
}
//这个是图不一定连通的
for(int i=0;i<n;i++)
{
	if(!dfn[i])
	{
		tarjan(i);
	}
}
//图连通时
//tarjan(0)

割点

如何求割点
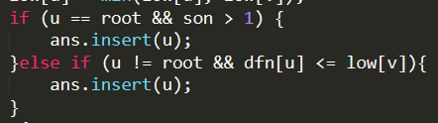
1.如果u是根节点，u必须有多个子树
2.如果u不是根节点，v是u的子节点，那么dfn[u]<=low[v]

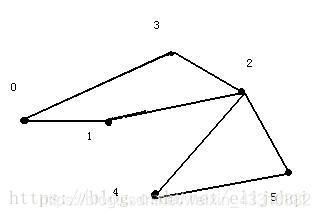
假设按以下顺序dfs，括号里表示的是回溯的过程
0-1-2-3-0(-3-2)-4-5-2(-5-4-2)-5(-2-1-0)-3(-0)
low和dfn比较：low[0]=low[1]=low[2]=low[3]=0
low[4]=low[5]=2
low和low比较：全部都是0…
问题出在low[5]上，如果是low[5]和dfn[2]比较low[5]=2，如果是和low[2]比较，low[5]=0
当low[5]=2的时候，2判断是割点，当low[5]=0的时候，2判断就不是割点了。
而实际上2是割点。
但是如果求强连通的时候大概影响无法体现 所以错误写法也是对的 但建议还是直接写dfn比较好

const int maxn=1e5;
int dfn[maxn],low[maxn],head[maxn],vis[maxn];
set<int >st;
int tot,cnt,num,root=1;
struct node{
	int v,nex;
}edge[maxn];

void init()
{
	fill(vis,vis+maxn,0);
	fill(dfn,dfn+maxn,0);
	fill(low,low+maxn,0);
	fill(head,head+maxn,-1);
	tot=0;
}

void tarjan(int u,int fa)
{
	dfn[u]=low[u]=++cnt;
	int son=0;
	for(int i=head[u];i!=-1;i=edge[i].nex)
	{	
		int v=edge[i].v;
		if(v==fa) continue;
		if(!dfn[v])
		{
			tarjan(v,u);
			son++;
			low[u]=min(low[u],low[v]);
			
			if(u==root&&son>1)
			{
				st.insert(u);
			}
			else if(u!=root&&dfn[u]<=low[v]) 
			{
				st.insert(u); 
			}
		}
		else
		{
			low[u]=min(low[u],dfn[v]); 
		}				
	}	
}

//这个是图不一定连通的
for(int i=0;i<n;i++)
{
	if(!dfn[i])
	{
	    root=i;
		tarjan(i,root);
	}
}
//图连通时
//root=0;
//tarjan(0,root)

割桥

如何求割桥
dfn[u]

他与求割点的代码就有一点小区别

割点代码

割桥

tarjan在图论中算是一个很基础但是用处又很广泛的一个算法，这篇文章主要总结tarjan算法中关于缩点的模板。
用处：我们通过tarjan算法，将所有强联通分量缩成一个点，即缩点。
总结：我们就是通过缩点将有向图转变为有向无环图，再通过有向无环图的性质来解决问题。
对于一个有向无环的图（DAG），至少添加几条边才能使它变为强连通图？我们很容易根据有向无环图的性质得到，我们计算入度为零的点数为a，出度为零的点数为b，那么我们至少需要添加的边数为max(a,b)，如果只有一个点的话，我们不需要添加任何边。

题目描述
给出一个 0 ≤ N ≤ 105 点数、0 ≤ M ≤ 105 边数的有向图，
输出一个尽可能小的点集，使得从这些点出发能够到达任意一点，如果有多个这样的集合，输出这些集合升序排序后字典序最小的。
输入描述:

第一行为两个整数 1 ≤ n, m ≤ 105，
接下来 M 行，每行两个整数 1 ≤ u, v ≤ 105 表示从点 u 至点 v 有一条有向边。
数据保证没有重边、自环。

输出描述:

第一行输出一个整数 z，表示作为答案的点集的大小；
第二行输出 z 个整数，升序排序，表示作为答案的点集。

示例1
输入
复制

7 10
4 5
5 1
2 5
6 5
7 2
4 2
1 2
5 3
3 5
3 6

输出
复制

2
4 7

#include
using namespace std;
const int inf=10000000;
const int maxn=1e5+10;
int n,m,head[maxn],tot=0;
int low[maxn],dfn[maxn],now=0,cnt=0,vis[maxn],belong[maxn];
//这个vis用来判断是否在队列中，用来判断是否便利过直接用dfn 
int minn[maxn];//用来记录字典序最小的值； 
stack<int>st;
struct node{
	int v;
	int next;
}edge[maxn];

vector<int>v;
int in[maxn];

void init()
{	
	fill(in,in+maxn,0);
	fill(head,head+maxn,-1);
	fill(minn,minn+maxn,inf);
}

void addedge(int u,int v)
{
	edge[tot].v=v;
	edge[tot].next=head[u];
	head[u]=tot++;
}

void tarjan(int u)
{
	dfn[u]=low[u]=++now;
	st.push(u);
	vis[u]=1;
	for(int i=head[u];i!=-1;i=edge[i].next)
	{

		int v=edge[i].v;
		if(dfn[v]==0)
		{
			tarjan(v);
			low[u]=min(low[u],low[v]);
		}
		else if(vis[v])
		{
			low[u]=min(low[u],dfn[v]);
		}
	}
	
	if(dfn[u]==low[u])
	{
		int x;
		cnt++;
		while(1)
		{
			x=st.top();
			st.pop();
			vis[x]=0;
			
			belong[x]=cnt;//新点
			minn[cnt]=min(x,minn[cnt]); //新点集合中最小的点 
			 
			if(x==u) break;			
		}
	}	
}


int main()
{
	init();	
	cin>>n>>m;	 
	for(int i=0;i<m;i++)
	{
		int t1,t2;
		cin>>t1>>t2;
		addedge(t1,t2);
	}
	for(int i=1;i<=n;i++)
	{
		if(dfn[i]==0)
		{
			tarjan(i);
		}
	}
	//便利新图，求各个新点的入度 

	for(int u=1;u<=n;u++)
	{
		for(int i=head[u];i!=-1;i=edge[i].next)
		{
			int v=edge[i].v;
			int u1=belong[u];
			int v1=belong[v];
			if(u1!=v1)
			in[v1]++;
		}
	}

	for(int i=1;i<=cnt;i++)
	{
		if(in[i]==0)
		{
			v.push_back(minn[i]);
		}
	} 
	sort(v.begin(),v.end());
	cout<<v.size()<<endl;
	for(int i=0;i<v.size();i++)
	{
		cout<<v[i]<<" ";
	}
	cout << endl;
		
}

SAT(Satisfiability)，n个变量每个变量可以取两种状态0/1。变量之间存在制约关系，能否选择一组满足所有制约关系的解。
将2-SAT转化为图，把每个点拆成两个点建边，tarjan判断可行 性。
同一个点两个状态都出现在同一个连通分量中无解
例题: Party
n对夫妻参加聚会，每对夫妻只能派一个人参加，夫妻间存在矛盾关系，问能否n个人都参加聚会?
把每个夫妻拆成两个点2i, 2i+1分别表示男女，如果1号夫妻的男和2号夫妻的女存在矛盾，那么当我们选择1号男参加party时，就要同时选择2号的男参加party;或者选择2号的女参加party,就要同时选择1号的女参加party。这样把n对关系用图表示，然后跑tarjan判断强连通分量是否存在矛盾-夫妻在同一个联通快中。