机器学习中的神经网络Neural Networks for Machine Learning:Lecture 5 Quiz
Lecture 5 QuizHelp Center
Question 1
For which of the following tasks can we expect that the problem of "dimension hopping" will occur (given that the data is input correctly)? Check all that apply.
Question 2
We have a convolutional neural network for images of 5 by 5 pixels. In this network, each hidden unit is connected to a different 4 x 4 region of the input image:
Because it's a convolutional network, the weights (connection strengths) are the same for all hidden units: the only difference between the hidden units is that each of them connects to a different part of the input image. In the second diagram, we show the array of weights, which are the same for each of the four hidden units.
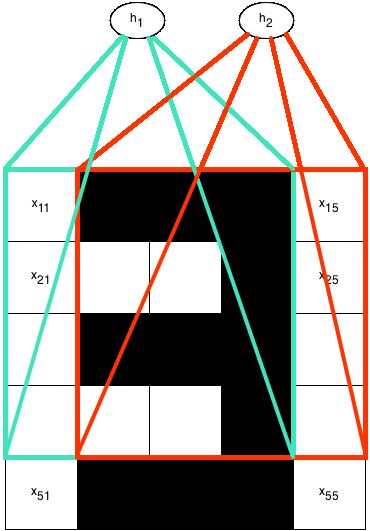
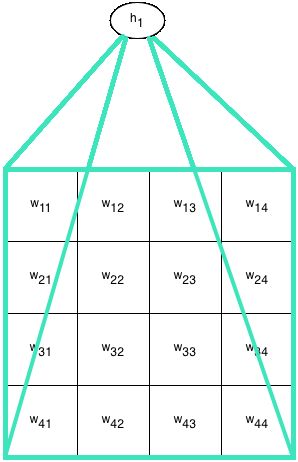
For h1 , weight w11 is connected to the top-left pixel, i.e. x11 , while for hidden unit h2 , weight w11 connects to the pixel that is one to the right of the top left pixel, i.e. x12 .
Imagine that for some training case, we have an input image where each of the black pixels in the top diagram has value 1, and each of the white ones has value 0. Notice that the image shows a "3" in pixels.
The network has no biases. The weights of the network are given as follows:
w11w21w31w41=1=0=1=0w12w22w32w42=1=0=1=0w13w23w33w43=1=1=1=1w14w24w34w44=0=0=0=0
The hidden units are logistic.
For the training case with that "3" input image, what is the output of each of the four hidden units?
- The first hidden unit, h1 , is connected to the upper left 4x4 portion of the input image (as shown below).
- The second hidden unit, h2 , is connected to the upper right 4x4 portion of the input image (as shown below).
- The third hidden unit, h3 , is connected to the lower left 4x4 portion of the input image (not shown in the diagram).
- The fourth hidden unit, h4 , is connected to the lower right 4x4 portion of the input image (not shown in the diagram).
Because it's a convolutional network, the weights (connection strengths) are the same for all hidden units: the only difference between the hidden units is that each of them connects to a different part of the input image. In the second diagram, we show the array of weights, which are the same for each of the four hidden units.
For h1 , weight w11 is connected to the top-left pixel, i.e. x11 , while for hidden unit h2 , weight w11 connects to the pixel that is one to the right of the top left pixel, i.e. x12 .
Imagine that for some training case, we have an input image where each of the black pixels in the top diagram has value 1, and each of the white ones has value 0. Notice that the image shows a "3" in pixels.
The network has no biases. The weights of the network are given as follows:
w11w21w31w41=1=0=1=0w12w22w32w42=1=0=1=0w13w23w33w43=1=1=1=1w14w24w34w44=0=0=0=0
The hidden units are logistic.
For the training case with that "3" input image, what is the output of each of the four hidden units?
Question 3
Recall that pooling is the process of combining the outputs of several hidden units to create a single hidden unit. This introduces some invariance to local transformations in the input image.
In this example we are pooling hidden units h1 , h2 , and h3 . Let's denote the output of hidden unit hi as yi . The hidden unit that we're creating by pooling is called hpool , with output ypool . Sum pooling is defined as ypool=y1+y2+y3 .
This form of pooling can be equivalently represented by making hpool a regular hidden unit that takes the output of the other three hidden units, multiplies them by some weights w1 , w2 and w3 , adds up the resulting numbers and then outputs some function of this sum. This is illustrated in the figure below.
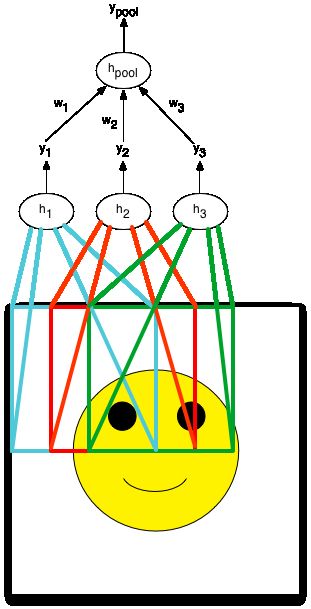
For this to be equivalent to sum pooling, what type of neuron should hpool be, and what should the weights be?
In this example we are pooling hidden units h1 , h2 , and h3 . Let's denote the output of hidden unit hi as yi . The hidden unit that we're creating by pooling is called hpool , with output ypool . Sum pooling is defined as ypool=y1+y2+y3 .
This form of pooling can be equivalently represented by making hpool a regular hidden unit that takes the output of the other three hidden units, multiplies them by some weights w1 , w2 and w3 , adds up the resulting numbers and then outputs some function of this sum. This is illustrated in the figure below.
For this to be equivalent to sum pooling, what type of neuron should hpool be, and what should the weights be?
Question 4
Suppose that we have a vocabulary of 3 words, "a", "b", and "c", and we want to predict the next word in a sentence given the previous two words. For this network, we don't want to use feature vectors for words: we simply use the local encoding, i.e. a 3-component vector with one entry being 1 and the other two entries being 0 .
In the language models that we have seen so far, each of the context words has its own dedicated section of the network, so we would encode this problem with two 3-dimensional inputs. That makes for a total of 6 dimensions. For example, if the two preceding words (the "context" words) are "c" and "b", then the input would be (0,0,1,0,1,0) . Clearly, the more context words we want to include, the more input units our network must have. More inputs means more parameters, and thus increases the risk of overfitting. Here is a proposal to reduce the number of parameters in the model:
Consider a single neuron that is connected to this input, and call the weights that connect the input to this neuron w1,w2,w3,w4,w5 , and w6 . w1 connects the neuron to the first input unit, w2 connects it to the second input unit, etc. Notice how for every neuron, we need as many weights as there are input dimensions (6 in our case), which will be the number of words times the length of the context. A way to reduce the number of parameters is to tie certain weights together, so that they share a parameter. One possibility is to tie the weights coming from input units that correspond to the same word but at different context positions. In our example that would mean that w1=w4 , w2=w5 , and w3=w6 (see the "after" diagram below).
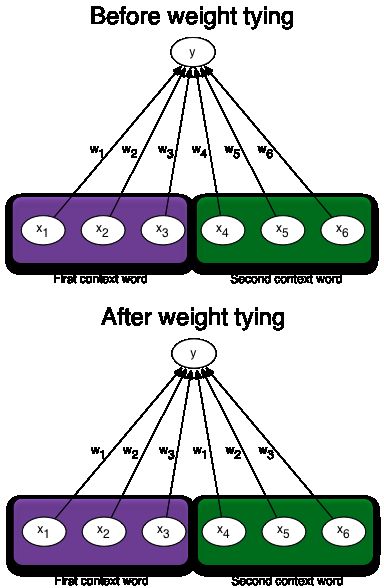
Are there any significant problems with this approach?
In the language models that we have seen so far, each of the context words has its own dedicated section of the network, so we would encode this problem with two 3-dimensional inputs. That makes for a total of 6 dimensions. For example, if the two preceding words (the "context" words) are "c" and "b", then the input would be (0,0,1,0,1,0) . Clearly, the more context words we want to include, the more input units our network must have. More inputs means more parameters, and thus increases the risk of overfitting. Here is a proposal to reduce the number of parameters in the model:
Consider a single neuron that is connected to this input, and call the weights that connect the input to this neuron w1,w2,w3,w4,w5 , and w6 . w1 connects the neuron to the first input unit, w2 connects it to the second input unit, etc. Notice how for every neuron, we need as many weights as there are input dimensions (6 in our case), which will be the number of words times the length of the context. A way to reduce the number of parameters is to tie certain weights together, so that they share a parameter. One possibility is to tie the weights coming from input units that correspond to the same word but at different context positions. In our example that would mean that w1=w4 , w2=w5 , and w3=w6 (see the "after" diagram below).
Are there any significant problems with this approach?
Question 5
Let's look at what weight tying does to gradients, computed using the backpropagation algorithm. For this question, our network has three input units, x1,x2,x3 , two logistic hidden units h1,h2 , four input to hidden weights w1,w2,w3,w4 , and two hidden to output weights u1,u2 . The output neuron y is a linear neuron, and we are using the squared error cost function.
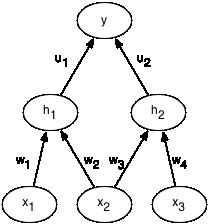
Consider a single training case with target output t . The sequence of computations required to compute the error (this is called forward propagation) are as follows:
z1=z2=h1=h2=y=E=w1x1+w2x2w3x2+w4x3σ(z1)σ(z2)u1h1+u2h212(t−y)2
E is the error. Reminder: σ(x)=11+exp(−x)
z1 and z2 are called the total inputs to hidden units h1 and h2 respectively.
Suppose we now decide to tie the weights so that w2=w3=wtied . What is the derivative of the error E with respect to wtied ?
Hint: forget about weight tying for a moment and simply compute the derivatives ∂E∂w2 and ∂E∂w3 . Now set ∂E∂wtied=∂E∂w2+∂E∂w3 .
Consider a single training case with target output t . The sequence of computations required to compute the error (this is called forward propagation) are as follows:
z1=z2=h1=h2=y=E=w1x1+w2x2w3x2+w4x3σ(z1)σ(z2)u1h1+u2h212(t−y)2
E is the error. Reminder: σ(x)=11+exp(−x)
z1 and z2 are called the total inputs to hidden units h1 and h2 respectively.
Suppose we now decide to tie the weights so that w2=w3=wtied . What is the derivative of the error E with respect to wtied ?
Hint: forget about weight tying for a moment and simply compute the derivatives ∂E∂w2 and ∂E∂w3 . Now set ∂E∂wtied=∂E∂w2+∂E∂w3 .
Question 6
Oh no! Brian's done it again! Claire had a dataset of 28 x 28 pixel handwritten digits nicely prepared to train a neural network, but Brian has gone and accidentally scrambled the images by re-ordering the pixels in some totally meaningless way, and now they can't get the original dataset back! Below is an image of a handwritten '2' before and after being scrambled by Brian.
Luckily, all of the images (in both the training set and the test set) were changed in the same way. For example, if pixels number 1 and number 3 switched places in one image, then they switched places in every other image as well. Because of that, Claire thinks that perhaps she can train a network after all.
Whether Claire is right or not depends largely on the type of neural network that she has in mind. Which of the following neural networks will be at a disadvantage because of Brian's mistake? Check all that apply.
| Before | After |
|---|---|
Luckily, all of the images (in both the training set and the test set) were changed in the same way. For example, if pixels number 1 and number 3 switched places in one image, then they switched places in every other image as well. Because of that, Claire thinks that perhaps she can train a network after all.
Whether Claire is right or not depends largely on the type of neural network that she has in mind. Which of the following neural networks will be at a disadvantage because of Brian's mistake? Check all that apply.