python打印n以内的质数--常见方法及效率对比

质数是指在大于1的自然数中，除了1和它本身以外不再有其他因数的自然数

传统方法

遍历就完事了，注意for-else结构，如果是for循环被break了，那么不执行else中的代码，如果遍历完了都没有触发break，那么执行else。按照这道题来说，即：如果能够在 [2，i）区间内找到一个j，使 i 能够被 j 整除，那么说明 i 不是质数，否则就是质数

def prime1(n):
    result=[]
    for i in range(2,n):
        for j in range(2,i):
            if i%j==0:
                break
        else:
            result.append(i)
    return result

输出结果：

if __name__ == "__main__":
    print(prime1(100))

方法2 减少遍历次数小优化

方法1的代码，每次判断i是否为质数时，都先判断i是否能够被比他小的数整除，判断次数为i-2次。然而，如果i能够被n整除，那么必存在一个m使i=nm，假设n<=m,那么必然是 n<=math.sqrt(i)<=m ( n²<= (nm) <= m²),所以我们可以先去找是否存在n，使i能够被n整除，如果n都找不到，自然也就没有m，所以可以判断i为质数,所以遍历范围可以写到（2，int(math.sqrt(i)+1)）即可

import math
def prime2(n):
    result=[]
    for i in range(2,n):
        for j in range(2,int(math.sqrt(i)+1)):
            if i%j==0:
                break
        else:
            result.append(i)
    return result

输出结果，依然是和方法1一样的。

另外一种优雅的写法是这样的，但是思路是一样的：
filter内的lambda函数：如果能够找到 i ,使x能够被 i 整除，那么就把i放入数组，如果最后数组不为空，说明x不是质数，那么返回false，否则返回true

def prime3(n):
    return list(filter(lambda x:not [i for i in range(2,int(math.sqrt(x)+1)) if x%i==0],range(2,n)))

方法3 进一步缩小比较范围

按照方法2，当我们判断16是否为质数时，我们需要计算：int(math.sqrt(x)+1)=5，也就是要在range(2,5)中比较。即3次（2,3,4）。然而事实上我们只需要比较2,3即可，因为能够被4整除的数，一定能够被2整除，所以比较4是多余的操作。当待判断的数更大时，这种冗余比较就会显得更加突出。基于这个思路很容易发现，我们要去判断的因子都应该是之前的质数。所以优化代码如下：
while -else 和for~else结构是相同的逻辑

def prime4(n):
    result=[]
    for i in range(2,n):
        if result==[]:
            result.append(i) 
            continue
        j=0
        while result[j]<(int(math.sqrt(i))+1):
            if i%result[j]==0:
                break
            j+=1
        else:
            result.append(i)
    return result

方法4 另一种思路

通过分析，很容易得出大于2的偶数一定不是质数，所以我们可以先把这部分数据筛选出来。具体代码如下：

def prime5(num):
    prime_boo=[False,False]+[True]*(num-2) # 先构造含长度为num的list，因为0,1不是质数所以填充False，其他填充True
    for i in range(3,num):
        if i&1==0: # 判断i是否为偶数，一点点优化也是时间嘛 (#^.^#)
            prime_boo[i]=False # 大于2的偶数不是质数，所以将下标为偶数的填充为false
    for i in range(3,int(math.sqrt(num)+1)):
        if prime_boo[i] is True:
            for j in range(2*i,num,i):
                prime_boo[j]=False #如果x是质数（true）,那么x的倍数就不是质数，全部置为false
    result=[]
    for k,v in enumerate(prime_boo):#值为true对应的index就是质数
        if v:
            result.append(k)
    return result

几种方法的效率对比

写一个打印时间的装饰器：

from functools import wraps
import time
def log(fn):
    @wraps(fn)
    def wrapper(*args,**kw):
        start=time.time()
        result=fn(*args,**kw)
        end=time.time()
        print('{} excute time:{}'.format(fn.__name__,end-start))
        return result
    return wrapper

打印四种结果花费的时间：可以看到四种方法结果完全一样，但是当n足够大时，prime5效率最高，prime1效率感人！

if __name__ == "__main__":
    r1=prime1(100000)
    r2=prime2(100000)
    r3=prime3(100000)
    r4=prime4(100000)
    r5=prime5(100000)
    print(r1==r2==r3==r4==r5)

上图看到方法4的效率还不如方法2高（需要比较的数字范围虽然少了，但是每次都是在result数组中取值，花费时间），但是当再加大n到1000W时，冗余比较的时间大于了从数组中取值的额外时间，此时方法4的效率是高过方法2的：

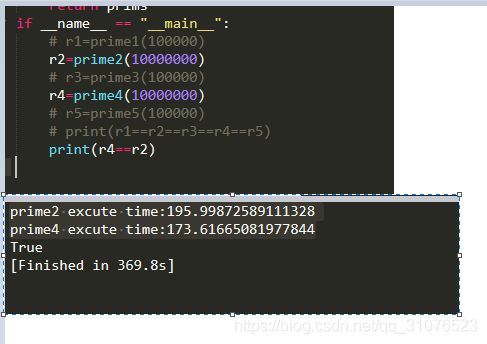
完整代码

import math
from functools import wraps
import time
def log(fn):
    @wraps(fn)
    def wrapper(*args,**kw):
        start=time.time()
        result=fn(*args,**kw)
        end=time.time()
        print('{} excute time:{}'.format(fn.__name__,end-start))
        return result
    return wrapper

@log
def prime1(n):
    result=[]
    for i in range(2,n):
        for j in range(2,i):
            if i%j==0:
                break
        else:
            result.append(i)
    return result
@log
def prime2(n):
    result=[]
    for i in range(2,n):
        for j in range(2,int(math.sqrt(i)+1)):
            if i%j==0:
                break
        else:
            result.append(i)
    return result

@log
def prime3(n):
    return list(filter(lambda x:not [i for i in range(2,int(math.sqrt(x)+1)) if x%i==0],range(2,n)))

@log
def prime4(n):
    result=[]
    for i in range(2,n):
        if result==[]:
            result.append(i) 
            continue
        j=0
        while result[j]<(int(math.sqrt(i))+1):
            if i%result[j]==0:
                break
            j+=1
        else:
            result.append(i)
    return result
@log
def prime5(num):
    prime_boo=[False,False]+[True]*(num-2)
    for i in range(3,num):
        if i&1==0:
            prime_boo[i]=False
    for i in range(3,int(math.sqrt(num)+1)):
        if prime_boo[i] is True:
            for j in range(2*i,num,i):
                prime_boo[j]=False
    result=[]
    for k,v in enumerate(prime_boo):
        if v:
            result.append(k)
    return result

if __name__ == "__main__":
    r1=prime1(100000)
    r2=prime2(100000)
    r3=prime3(100000)
    r4=prime4(100000)
    r5=prime5(100000)
    print(r1==r2==r3==r4==r5)

补充：C语言素数筛，非常巧妙

int prime[MAX_N+5]={0}; //0代表素数，1代表合数
//求m以内的素数
void init_prime(int m){
    for (int i=2;i<=m;i++){
        if(prime[i]) continue; //如果是合数，跳转到下一个循环
        prime[++prime[0]]=i; //如果是质数，那么首尾+1，第1位存第一个质数，第二位存第2个质数……
        for(int j=i,I=m/i;j<=I;j++){        	
            prime[i*j]=1; //如果是质数，那么它的倍数就是合数。
        }
    }
}

这种方法巧妙之处是，首位计算满足条件个数，后面依次记录对应的质数，省去了c语言单独求int数组的长度问题。但是在标记质数的倍数为合数时存在一定重复计算。如：i=2，标记位:2 * 2,2 * 3……为合数。 i=3时，标记位：:3 * 3,3 * 4，3 * 5.为合数。可以看到2 * 6=3 * 4。

针对上述重复计数，一个更烧（骚）的方法产生了：

int pirme[1000]={0};
void init_prime(int m)
{
    for (int i = 2; i <= m; i++)
    {
        if (!prime[i])
            prime[++prime[0]] = i;
        for (int j = 1; i * prime[j] <= m; j++)
        {
            prime[i * prime[j]] = 1;
            if (i % prime[j] == 0)
                break;
        }
    }
}

整体思想一致，假设计算30以内的质数，程序执行流程罗列如下：
i=2,prime[2]=0 => prime[0]=1,prime[1]=2; ⇒ j=1, prime[2 * 2]=1;
i=3,prime[3]=0 => prime[0]=2, prime[2]=3; => prime[3 * 2]=1,prime[3 * 3]=1;
i=4, prime[4]=1 => 不记录 ⇒ prime[4 * 2]=1;
i=5,prime[5]=0 => prime[0]=3,prime[3]=5; ⇒ prime[5 * 2]=1,prime[5 * 3]=1,prime[5 * 5]=1
i=6, prime[6]=1 => 不记录 ⇒ prime[6 * 2]=1;
i=7,prime[7]=0 => prime[0]=4,prime[4]=7; ⇒ prime[7 * 2]=1,prime[7 * 3]=1
i=8, prime[8]=1 => 不记录 ⇒ prime[8 * 2]=1
i=9, prime[9]=1 => 不记录 ⇒ prime[9 * 2]=1;prime[9 * 3]=1;
i=10, prime[10]=1 => 不记录 ⇒ prime[10 * 2]=1
i=11, prime[11]=0 => prime[0]=5,prime[5]=11; ⇒ prime[11 * 2]=1
i=12, prime[12]=1 => 不记录 ⇒ prime[12 * 2]=1
i=13, prime[13]=0 => prime[0]=6,prime[6]=13; ⇒ prime[13 * 2]=1
i=14, prime[14]=1 => 不记录 ⇒ prime[14 * 2]=1
i=15, prime[15=1 => 不记录 ⇒ prime[15 * 2]=1
…………………………
i=15时，输出的prime为：{6,2,3,5,7,11,13,0,1……}

可以看到，再根据质数标记合数时，没有重复项。非常nice！